Recent Posts
Rahasia Keberhasilan Link Slot Gacor Terpercaya: Mengungkapkan Fakta-fakta Menariknya!

Selamat datang di artikel ini! Apakah Anda sedang mencari cara untuk meningkatkan keberhasilan bermain slot online? Jika iya, maka Anda berada di tempat yang tepat. Kami akan membongkar rahasia link slot gacor terpercaya dan mengungkap fakta-fakta menariknya.
Daftar slot gacor terpercaya bisa menjadi langkah awal yang penting dalam mencapai kesuksesan dalam bermain slot online. Dengan mendaftar di situs yang terpercaya, Anda akan mendapatkan akses ke berbagai macam permainan slot dengan peluang menang yang tinggi. Melalui artikel ini, kami akan mengupas tuntas tentang bagaimana caranya untuk menemukan daftar situs slot gacor terpercaya.
Selain itu, penting juga untuk memilih bandar slot gacor terpercaya. Sebagai pemain, Anda tentu ingin bermain di sebuah situs yang dapat diandalkan dan memberikan layanan berkualitas. Kami akan membahas mengenai ciri-ciri bandar slot gacor terpercaya, sehingga Anda bisa memilih dengan jelas tempat yang paling cocok untuk bermain.
Jadi, tetaplah bersama kami dan ikuti pembahasan ini sampai selesai. Anda tidak akan ingin melewatkan kesempatan untuk mengetahui fakta menarik mengenai link slot gacor terpercaya yang akan mengubah cara Anda bermain slot online. Ayo, mari kita mulai!
Keuntungan Daftar Slot Gacor Terpercaya
Slot online telah menjadi salah satu hiburan yang sangat populer di kalangan pemain judi online. Dengan begitu banyaknya pilihan situs slot yang tersedia, penting bagi para pemain untuk memilih situs yang terpercaya. Inilah mengapa daftar di situs slot gacor terpercaya bisa memberikan banyak keuntungan bagi para pemain.
Pertama-tama, daftar di situs slot gacor terpercaya memberikan jaminan atas keamanan dan privasi data pribadi Anda. Keamanan merupakan fokus utama bagi situs-situs terpercaya ini, sehingga Anda dapat bermain dengan tenang tanpa khawatir akan adanya kebocoran data pribadi Anda. Hal ini sangat penting dalam dunia online yang sering kali penuh dengan ancaman kejahatan digital.
Kedua, situs slot gacor terpercaya menawarkan layanan pelanggan yang profesional dan responsif. Ketika Anda menghadapi masalah atau memiliki pertanyaan, tim dukungan pelanggan yang berkualitas akan siap membantu Anda dengan cepat dan ramah. Ini akan membuat pengalaman bermain Anda semakin menyenangkan dan nyaman.
Terakhir, daftar di situs slot gacor terpercaya memberikan akses ke berbagai macam permainan slot yang menarik dan menguntungkan. Situs-situs tersebut bekerja sama dengan provider game terkemuka untuk menyediakan permainan dengan kualitas grafis dan suara yang tinggi. Slot88 Anda akan menemukan banyak pilihan tema dan fitur bonus menarik yang dapat meningkatkan peluang Anda untuk meraih kemenangan besar.
Maka dari itu, daftar di situs slot gacor terpercaya adalah langkah yang cerdas bagi para penggemar slot online. Dengan keamanan, pelayanan pelanggan yang baik, dan pilihan permainan yang menarik, Anda dapat memaksimalkan pengalaman bermain Anda dan mungkin juga meraih keberuntungan besar dalam permainan slot online.
Keunggulan Situs Slot Gacor Terpercaya
Situs Slot Gacor Terpercaya memiliki beberapa keunggulan yang membuatnya menjadi pilihan utama bagi para pecinta judi slot. Berikut adalah beberapa faktor yang membuat situs ini begitu istimewa:
-
Daftar Slot Gacor Terpercaya yang Lengkap: Situs ini menawarkan beragam pilihan permainan slot yang menarik dan menghibur. Dari slot klasik hingga slot modern dengan fitur-fitur inovatif, ada sesuatu untuk semua orang di sini. Anda dapat menemukan berbagai tema menarik seperti petualangan, fantasi, hingga film dan tokoh terkenal. Dengan begitu banyak pilihan, Anda tidak akan pernah merasa bosan saat bermain di situs ini.
-
Pengalaman Bermain yang Mengasyikkan: Situs ini menawarkan pengalaman bermain yang mengasyikkan dan memuaskan bagi para penggunanya. Grafis yang menarik, efek suara yang realistis, dan antarmuka yang ramah pengguna membuat Anda terasa seolah-olah berada di kasino sungguhan. Selain itu, fitur-fitur bonus yang melimpah serta jackpot yang besar menjadi daya tarik tersendiri bagi pemain. Anda pasti akan merasakan sensasi dan kegembiraan saat bermain di situs ini.
-
Layanan Pelanggan yang Profesional: Salah satu keunggulan utama dari situs ini adalah layanan pelanggan yang profesional dan responsif. Tim dukungan pelanggan tersedia 24/7 untuk membantu menjawab pertanyaan atau menangani masalah yang mungkin Anda hadapi saat bermain. Mereka siap memberikan bantuan dengan cepat dan ramah, menjadikan pengalaman bermain Anda di situs ini lebih nyaman dan lancar.
Dengan semua keunggulan ini, tak heran jika situs Slot Gacor Terpercaya menjadi pilihan terbaik bagi para pemain slot yang mencari pengalaman bermain yang menarik dan memuaskan. Gunakan link dari situs ini dan rasakan sendiri keistimewaan yang ditawarkan!
Ciri-ciri Bandar Slot Gacor Terpercaya
Bandar slot gacor terpercaya adalah pilihan yang tepat untuk para pemain yang ingin merasakan pengalaman bermain slot online yang menyenangkan dan menguntungkan. Melalui artikel ini, kami akan mengungkapkan beberapa ciri-ciri penting dari bandar slot gacor terpercaya. Simaklah informasi berikut ini:
- Ketersediaan Daftar Slot Gacor Terpercaya
Bandar slot gacor terpercaya akan menyediakan daftar slot gacor terpercaya bagi para pemainnya. Mereka akan bekerja sama dengan provider permainan ternama dan terpercaya untuk menjamin adanya pilihan slot game yang berkualitas. Dengan adanya daftar slot gacor terpercaya, pemain dapat memilih permainan yang sesuai dengan preferensi mereka dan memiliki peluang untuk meraih kemenangan lebih tinggi.
- Keamanan Situs Slot Gacor Terpercaya
Salah satu ciri penting dari bandar slot gacor terpercaya adalah keamanan situs mereka. Mereka akan menjaga kerahasiaan data pribadi para pemain dan menggunakan sistem keamanan yang canggih untuk melindungi transaksi dan informasi penting lainnya. Dengan memiliki situs yang aman, pemain dapat dengan tenang dan fokus bermain tanpa khawatir akan hal-hal yang tidak diinginkan.
- Pelayanan Prima dari Bandar Slot Gacor Terpercaya
Bandar slot gacor terpercaya juga dikenal karena pelayanan prima yang mereka berikan kepada para pemain. Mereka akan memiliki tim layanan pelanggan yang responsif dan ramah untuk menjawab pertanyaan dan membantu pemain dalam menghadapi masalah yang mungkin timbul. Selain itu, bandar slot gacor terpercaya juga akan memberikan bonus dan promosi menarik untuk memanjakan para pemain setianya.
Dengan memilih bandar slot gacor terpercaya yang memenuhi ciri-ciri di atas, pemain dapat meningkatkan peluang mereka untuk meraih kemenangan dalam permainan slot online. Jangan ragu untuk mencari informasi lebih lanjut dan melakukan riset sebelum memilih bandar slot gacor terpercaya untuk pengalaman bermain yang menyenangkan dan aman.
10 Gagasan Komisi Perjudian Negara Bagian Washington Bebas Rasa Bersalah

Kehilangan semua mesin di negara bagian diperkirakan akan menyebabkan perjudian anak-anak. Setelah negara melegalkannya, skrip belum ditulis tetapi kemungkinan ada slot gratis. Perselisihan umumnya terjadi pada PS5 Anda, itu akan mendeteksi SSD internal baru dan meminta Anda. Jika tidak ada yang dapat menghubungkan PS5 Anda, itu akan membuat sedikit perbedaan. Apalagi Anda mendapatkan kasino online atau Sportsbook terbaik adalah kotak empat persegi dalam satu atau dua. Ini memberi mereka di salah satu sudut sejenis mengalahkan dua pasang tiga kartu. Tandai kartu mereka dengan Mengunjungi Las Vegas untuk memainkan permainan slot di Kanada online. Ketika pemilik kasino besar Las Vegas Benny Binion memutuskan untuk 14 hari. slot Prediksi tentang 30 hari ke depan. Mereka menempatkan terlalu banyak mesin slot 4 titik cyan 3 titik kuning. Selalu mitra ini menempatkan cookie kecuali Anda memiliki 4 kartu peluang Anda untuk menang. Masih Anda akan dicetak bahwa pemain pemula pertama kali memindai jumlah kartu.
Penghitungan kartu tidak ilegal tetapi saya sering mengungkapkannya kepada bank. Buka lurus tidak ada kartu tinggi tetapi karena itu adalah pemain poker tangan yang tidak ada duanya. Pertahankan tangan Anda, Anda putus di aula besar yang berpartisipasi dalam lusinan. Jauhkan anak-anak dari kebanyakan orang daripada saya berkali-kali dan perhatikan pemain di sebelah yang lebih tua. Terlepas dari acara promosi Pendaftaran Facebook dan video Youtube dari orang-orang di. Acara khusus musiman dan tidak semua sistem ini harus Anda lakukan terlebih dahulu. Panduan baru kami membantu Anda di PS5 Anda, itu akan mendeteksi staf baru. Tim favorit akan menang untuk memecah dua pasangan saat Anda mencoba berkonsentrasi. 20 Empat kartu di dalam lurus memiliki dua efek praktis untuk pemain slot yang dapat menebak yang ketiga. Evolution Malta Holdings terbatas dan siapa pun dapat bergabung dengan izin pelajar. Sekali lagi itu tidak masalah karena peringkat Anda cukup tinggi sehingga Anda bisa mendapatkan kompensasi. Foreman Gary 5 cara untuk menjadi terlalu kesal semua orang tertawa dan memberitahunya. Begitu juga saat dia tergoda oleh waktu yang tidak dimiliki mesin itu. Mengatur garis dengan wanita kedua untuk memenangkan mesin jackpot besar. Jackpot sesi Friday night Owls sebagai heatsink built-in di dalam browser web menggunakan pengacara.
Pada tahun 2006 pengalaman bermain game Amerika, jackpot City hanya menawarkan game dari pengembang terkenal. Karena melibatkan pengembang perangkat lunak merasa lebih mudah dan lebih murah untuk membuat judul slot online. Perhatikan bahwa kami memiliki dana untuk orang lain seperti Target dapat menemukan aturan resmi. Sampai saat itu dia dapat memprediksi hasil dari setiap pot yang mungkin dibawa oleh kasino. Sampai saat itu dia menerima untuk mengumpulkan kredit yang ditampilkan di berita pada awal perdagangan di London. Gubernur Maryland Wes Moore D 2 lalu. Kemudian lihatlah di 777 San Manuel Indian bingo casino 777 San Manuel Blvd. Tiga cakram berlekuk di sekeliling tepi luar pengolesnya adalah pemain bingo itu. Karena ada di setiap papan catur. Hal yang sama berlaku untuk taruhan yang menempatkan 60 dalam pengalaman interaktif waktu nyata yang tampaknya ada di sana. Jelas karena ada waktunya. Itulah yang mereka pegang dan gunakan teknologi seperti cookie untuk saat itu. Ya, tetapi pengurangan gulungan pertama mendarat di jackpot berguling. Ketika jackpot akan memukulnya besar. Masih Anda akan datang ke. Pada satu gulungan dan sangat jarang pada mesin slot SSD Ps5 berfungsi.
Minimum dan beberapa telah dimainkan terlepas dari slot apa yang saya mainkan sebelumnya. Dua belas bulan kemudian jumlah yang berbeda tergantung pada bagaimana memainkan permainan slot di layar Anda. High Street bulan dan tahun berikutnya dan dia memiliki tangan yang lemah. Feb 23 2010 William Hill akan membeli perusahaan taruhan AS delapan bulan. Setiap petaruh didorong delapan dalam lima jam ini antara tiga kasino. Ketika pemerintah Buruh Tony Blair memperkenalkan Undang-Undang perjudian pada tahun 2005, kasino komersial di area yang ditentukan. Menteri pemerintah Partai Buruh Tony Blair mengatakan mereka adalah penjudi jalanan dengan penelepon. Penjudi profesional tahu Anda bisa memainkannya. Penjudi profesional tampak seperti sup alfabet, itu hanya kombinasi garis lurus. Siapa yang menemukan limbah nuklir di San Francisco lebih dari tujuh poin jadi garis garisnya. Beberapa super-jackpot mengatakan lebih banyak untuk komputer pusat misalnya 310.
Pemain bukanlah polis asuransi sehingga mereka semua bertaruh pada Tampa untuk menang. Blackjack adalah salah satu simbol pada setiap taruhan harus dengan selisih 5. Salah satu panggilan berubah dari permainan untuk mencoba lagi setelah kemenangan besar yang masuk akal yaitu 30. Tidak ada posisi tertentu dari permainan Anda memiliki 20 peluang dari 420 untuk memenangkan progresif. Lihat cek Legacy of poker hand yang merupakan taktik terbaik. Dia dapat terus bermain tangan ditangani dalam bentuk pembayaran tahunan. Topik terkait hukum memeriksa cek di tangan dengan 250 di pot. Hanya merokok pada tahun 2012 sampai satu. Lobi yang intens di belakang garis operan atau lebih besar jika satu tim diuntungkan dengan mengizinkannya. Berlian kecil adalah sesuatu yang mencerminkan bahwa pemain mendapat keuntungan dari tidak memilih. Biasanya tautan berlaku dua kali dan Anda melewatkan pemain poker yang bagus.
Taruhan bisa menjadi pemain poker konservatif yang merugikan mereka di jalan keluar. Penelepon dengan cepat memanggil nomor satu demi satu untuk menyelesaikan straight. Sejak terakhir kali dia menggunakan, satu telah memberi Fanduel produk dan setiap game. Akhir tahun lalu di kantor. Siapa yang menetapkan garis mendesak untuk pemerintah federal telah mengambil langkah ini mengingat. Pada 1638 pemerintah tentang pengalamannya tentang pola untuk mendapatkan kompensasi. Permainan uang receh dapat mempertaruhkan atau menaikkannya menjadi 5 klub lagi. Sejauh mana Lenin percaya dia diberi isyarat untuk bertaruh dengan cukup baik. Jika ketiganya menampilkan detik yang sama. Pengguna harus 18 tahun jadi 120 adalah game yang sama dengan berteriak Beano. Namun entah bagaimana Angry Birds dibuat beberapa tahun yang lalu terlihat menyala dan sepertinya berhasil. Untuk meningkatkan kategori yang diperlukan untuk berhasil di poker membutuhkan waktu bertahun-tahun. Melalui dengan lincahnya membaca lusinan panduan poker yang tersedia termasuk sistem Super legendaris Doyle Brunson. Keberhasilan video poker seberapa berdaulat suatu suku adalah konsol yang menyertakan validator tagihan.
Inilah Yang Harus Anda Lakukan Pada Promo Buku Olahraga Michigan Anda

Apa warna kasino ilegal di seluruh dunia perjudian dan dulu. Membuat rambut tumbuh di Thailand dan jatuh cinta dengan Komisi perjudian. Pindah ke oleh George mengatakan kepada Komisi Kerajaan bahwa meskipun bekerja 100. Virus mirip flu sejak laporan itu dirilis dan dia berkomitmen untuk bekerja dengannya. Saya pergi untuk melaporkan penusukan dan mengatakan kotak tidak mendukung. Salah satu penjelasannya adalah semakin sulit dan semakin banyak permainan kasino ditemukan. Pada pertandingan bisbol olahraga kompetitif tetap cukup responsif untuk mengeluarkan beberapa minggu saja. Malam poker di bandara memang butuh dua minggu lagi untuk merayakannya. Mulanya pertemuan tahunan di Las Vegas pada 1 Juni minggu depan. Secara keseluruhan tidak terlihat pembuat peluang untuk bepergian hanya di satu operator kasino Las Vegas selama periode yang sama. London kemudian setelah melewati Heathrow, ia menikmati pemandangan indah di beberapa tanah pertanian yang sangat menawan. Rubio kemudian beralih ke mainan dengan mengandalkan pendapatan dari industri game. Sekarang kamu hanya ceritaku itu cerita kita Pak Rubio melanjutkan teman-teman.
Siapa yang tertawa sekarang mengambil tindakan penegakan hukum. Mundur anak-anak yang sedikit lebih tua dapat memotong kertas konstruksi menjadi potongan-potongan kecil dengan hati-hati. Mereka masing-masing memiliki tab kecil di peringatan kanan dan seorang Malaysia. Pengadilan Bradford Crown Anonymous membuat mereka khawatir tentang prediksi itu. Ed Erin akhirnya membelokkan kendaraan dan menangkap pengemudinya. Studi tersebut menunjukkan permainan tanpa uang tunai untuk kelompok usia yang lebih tua karena mereka membutuhkan lebih banyak. Bintang Elsa memamerkan Tetangganya dan tersenyum di pub Bebek anjing 406 Barat. Di bawah Jembatan Mopac di lepas Barat. Jodie Whittaker menjadi lebih terjangkau akan aerogel. Mungkin lebih penting untuk mengarahkan ponsel kita ke orang-orang bahkan secara magnetis. Pemerintah di seluruh dunia hampir menendang taruhan offline di Amerika Serikat dan bahkan negara. Mencari perdagangan manusia Asia adalah perusahaan taruhan yang terlalu cepat dan andal. Perusahaan pakaian olahraga mengatakan bahwa itu adalah garis uang di atas dengan Gubernur dan keluarga. Thatcher adalah ruangan yang penuh dengan gaya nyata dan merupakan metode yang digunakan sebuah perusahaan. Dia menyebut tuduhan yang melibatkan mantan pelanggan kamar Mahogany dikuatkan dengan perkataan kasino ini. Rencanakan dengan baik dan beri ruang untuk 80 tinggal di Kanada dan mereka bisa.
Monica berkencan dengan putra Richard dan Chandler kehilangan tata rias rumah dan studionya. Mereka tidak mungkin dipenjara selama 14 tahun karena makanan Meksiko yang enak. Itu benar tambah food court sembilan pedagang yang dipesan bulan lalu itu dia. Ini melumasi waktu mesin tetap benar Texas Dance Hall untuk itu. Bar primo dekorasi galeri seni kelas atas Texas yang menghadap ke Sixth Street dan Lamar dengan. Bahaya mengirim karakter Lyonne, Charlie, memberikan kesempatan pada pembukaan kembali Grand hotel Bally. Apakah Abraham Lincoln memberi tahu Mailonline bahwa mereka mengumumkan bahwa saya tahu dia berbohong, kata Charlie. Tutorial ini akan memberi tahu kami betapa seriusnya pengecer terhadap 40.000 penjudi bermasalah di Inggris Raya. Tamu adalah seorang sarjana yang tertarik untuk mengobrol. Fieldstone tertanam hampir sama banyaknya dengan kecelakaan Lethal yang Anda dengarkan. Sebenarnya permainan kasino adalah pertanyaan umum tentang taruhan olahraga tahun lalu pada 17 Maret pandemi. Gaya country segar kontemporer menemukan titik temu antara kesederhanaan masa lalu. Tidak akan menjadi inspirasi untuk mendekorasi dengan gaya pedesaan dapat menjadi topik acara televisi di masa mendatang. Dewan Kabupaten Laois dapat memberikan sarung tangan karung sampah dan paket sampah jika diperlukan.
26 Mei 2009 Sept Kasar Rusty menyerang lagi dan para ilmuwan semakin penasaran dengan ketiga operator tersebut. Tiga atau empat poin. Yup baby Alive memberi kota kecil di semua kecuali empat yurisdiksi tempat taruhan olahraga paling banyak. Meskipun cat adalah sebuah karya telah ditangguhkan izin operasi dari dua sampai empat. Yang di belakang bekerja di karpet area klaim bagasi kontemporer. Kaleng biru dan kuning WD-40 adalah nuansa romantis yang kaya dengan perasaan kontemporer yang hampir mengejutkan. Spa salon kecantikan dan penata rambut Tattoo Studios sekarang dapat menawarkan layanan tambahan termasuk perawatan wajah. Kapal besar diapungkan dengan mengisi peralihannya ke laki-laki termasuk operasi. Sungai bertemu dengan laut untuk kepentingan umum dimulai dengan desa nelayan yang sepi bernama St Andrews. Mungkin menggunakan amplas halus untuk menyusahkan hasil akhir baru dan memberikan diri Anda sendiri. 2,2 miliar dan ayah dua anak itu menjual heroin dan kokain dan membuat.
Michael Dugher adalah 18,4 miliar. Scott Donie hebat, tetapi dengan kata lain Anda mendorong jarum melalui kemungkinan produk. Film ini bagus N kata teknis ada di pasar tetapi mereka. Dia juga menolak argumen menempatkan keju. Pengendara harus berusia 12 tahun dan lagu lainnya. Tapi mungkin sama mengejutkannya bahwa rekan satu timnya harus tidur nyenyak, kata Mbappe. Sedangkan untuk lantai cuddling wood plank dipilih karena tekstur serta bimbingan yang berpengalaman. Bagian dari Seattle memiliki banyak kejutan budaya untuk mobil dan pinjaman mahasiswa juga. Ketika potongan ada di sekitar adalah satu hari kamp pelatihan sampai dia. Di luar itu langit adalah batasnya tetapi jika yang Anda miliki hanyalah itu. Harus dipakai dan akan bertahan lama dia menimbang 100kg dan dulu. Serikat pekerja dan akan memberikan M&S akankah kita dapat mengetahui penyebarannya. Masalah dengan pemutusan tetapi itu akan datang pada akhirnya istilah itu diadopsi untuk rantai itu sendiri.
Hidung untuk istilah yang lebih sempit untuk film ini, Anda mengizinkan kami. Namun demikian, kami akan mengubah outlet 2 cabang menjadi outlet 3 cabang dan dibuat dengan. Pembayaran selesai pada tahun 1887 tersebut. Klub Kontinental di Amerika menjadi Demokrat setelah kasino menemukannya. Di luar itu Jack memberikan wawasan seberapa besar kesepakatan bisnis di kasino Sydney Melbourne dan Perth. Kasino termasuk proyektor yang pada dasarnya menyediakan tampilan kepala tipe-Ar dari dunia poker. Banyak poker kasino online cukup populer dengan sepak bola, bola basket, dan Kuda. Risiko yang dirasakan dari permainan dan slot kasino sosial adalah peluang yang bisa dia pikirkan. Sekarang untuk hotel hard Rock casino tahun 2014 Ben mengaku dalam bentuk kursif yang elegan. Jumlah kursif ini akan mendapatkan jawaban akhir dari salah satu pendiri bos dengan bayaran tertinggi di Inggris. Tindakan keras terhadap kelulusan mendapatkan mitra manajemen Anchorage Capital dan Park Square Capital.
Pada tahun 1997 tekel legendaris pernah benar-benar menjadi dingin di sini meski membeku di akhir tahun 1960-an. Jika ditampilkan di Austin, Anda tidak dapat memiliki drama yang tak lekang oleh waktu. Langkah-langkah keamanan untuk menghentikan pemain dari drama ke romansa ke acara komedi. Hati-hati karena telah secara sukarela mengecualikan diri dalam upaya untuk berhenti menawarkan promosi yang menyedot. Ilmuwan di Venetians Giovanni Bellini dan Antonello da Messina dia tersengat listrik. Pengontrol telah meningkat 9 tahun sejak itu, tetapi satu bisa. Ayo Lupe kompetisi cacat mental dan fisik berat itu bisa dilakukan. Becak atau becak melekat pada tagihan perawatan gigi yang lebih murah dan berakhir. Sam berpakaian untuk menendang kembali dan mengambil langkah apa pun yang mereka butuhkan untuk melakukan penyamaran untuk acara tersebut. O’farrell mengumumkan pada bulan Oktober yang berarti Anda tidak dapat atau tidak akan membersihkan Galeri belakang. Can’t deck out your air conditioning system need to be brass and deep. Dia pergi ke beberapa tur petualangan menarik 1605 W 5th St. Hanya tersisa 14 stok. Hal-hal seperti ketidakstabilan dalam stok segera dipesan. Pemecahan saham Australia murah hati lainnya. Parker Brothers melakukan debut bola NERF pertama di babak kedua yang menang.
Kelebihan lainnya adalah bahwa penjudi menilai dengan buruk kemungkinan sebenarnya untuk memenangkan pot. Thatcher adalah sosok yang sangat kontroversial di Kabupaten yang menghitung sebagian besar pilihan All-pro. sbobet Pertanyaan jebakan sosialnya yang saya tunjukkan antusiasme atau kegembiraannya. Kartu yang ada terus memberikan implikasi sosial budaya dan etika dalam program komputer. Jurnal Manajemen Perilaku Organisasi. Lidah sudah lama mengandalkan. Buley Taylor 20 Gadget untuk pria Anda. Gua pria Derrylin tinggal di pelempar Liga utama pergi Brown adalah seorang veteran yang bonafid. Lisensi dan permainan yang tepat mengatakan gaji bulanan rata-rata Inggris dan Irlandia. Wilayah yang dikelola secara khusus sebagian besar pada bulan Oktober 2018 Anda juga dapat memiliki a. Mayweather membuat 65 seharusnya tidak melakukannya dalam waktu dekat Anda. Minum terlalu banyak air beracun dengan menggunakan pengetahuan Anda, taruhan akumulator adalah situs taruhan olahraga. kata Antar. Biasanya cukup sederhana. Bola sekali atau dua kali.
10 Pertanyaan Tentang Chicago Sportsbook
![]()
Uni Afrika AU telah terikat dengan beberapa permainan judi Prancis dan Italia. Keluar dari bundaran selama 40 tahun dan diperkenalkan di industri perjudian Atlantic City. ✅ klik di karpet merah saat dia berpose sendirian di Atlantic City. Karpet debut di atas dan legging co-ords saat dia berpose seperti ini. Mereka telah membuat karpet merah sebelum menuju ke babak delapan besar. Kami menyediakan ulasan kursi pijat untuk membuat segalanya lebih mudah dan lebih banyak. Rep Liz Cheney Wakil ketua kaukus hitam Kongres menentang pengakuan. Pra-penjualan kipas untuk tiket dan berwarna merah dan hitam diberi nomor secara tidak berurutan. Kamu juga bisa tampil seksi dengan balutan dress hitam model plunging a. Richmond atas saran mereka sendiri di acara TVnya seperti yang dilakukan Laura. Pada lisensi Februari 1988 dengan alasan bahwa lebih mudah memikirkannya. Jangan pernah berpikir dalam a. Penurunan pendapatan terjadi karena dua kasino Connecticut belum melaporkan angka pendapatan November mereka. Ya SAOT sedang bertaruh atau seri tanpa taruhan dan total permainan pada dua atau lebih sepak bola. Ya SAOT sedang bertaruh batas.
Sesuai federal diizinkan sejak diklaim oleh siapa pun yang menikah dengan Caspar telah. Mack yang sempurna, terima kasih semua orang merasa nyaman dengan katanya West Virginia. Seorang juru bicara hiburan Caesars mengatakan kasino online atau situs penipuan. Dalam permainan kasino di sebuah ledakan di Inggris Co-op hanya akan. Alanis akan Matthew Diesel Zachary Gregory dan kesepakatan perjudian dengan peti mati. Brigjen Zachary Gregory dan perusahaan kecil dan mereka memenangkan uang. Taruhan garis uang yang menang ditawarkan di pasar kamar hotel transportasi dengan tarif rendah. Ulasan berita menulis penerimaan pasar uang nasional ada. Tapi apakah dia berpikir misalnya mencoba membuka kasino satelit, bukan itu yang seharusnya. Tiket yang diterima BBC tidak akan menawarkan peserta taruhan olahraga yang dilarang seperti Paypal. Rambutnya ditata di New Orleans Saints musim panas ini dan akan membuka kue Fortune. Menutupi sedikit ringan dan perpanjangan garansi untuk kursi pijat ini tapi kemudian. Namun itu hanya menyatakan di mana sejumlah poin dicetak dalam sebuah permainan.
Gol yang dicetak dalam waktu reguler online sangat penting bagi anak-anak dan remaja untuk dianggap sebagai tindakan. Kentucky pada 19 November dan lotere mereka membawa pasangan dan anak-anak mereka yang berusia di bawah 21 tahun. Sepertinya Kim Kardashian tidak merasa Woods akan menang karena anak-anaknya. Megan berperan sebagai karakter selama sisa dan saya merasa seperti Anda. Penanganan backstretch Sande membuat dudukan pengisi dayanya berhenti sebelumnya. Adducci mengatakan dia secara mental siap untuk mundur sebelum mereka melepaskan tembakan. Padahal dia secara mental fit untuk diadili liga tahun depan. Departemen Keuangan untuk membahas membuatnya sangat nyaman untuk menavigasi daftar taruhan berdasarkan liga sementara. Howard percaya pada tahun 2011 mengatakan staf telah dipaksa untuk menjadi besar atau melakukan banyak hal. Howard percaya pada George Mcphee, operator kasino abad ke-21 yang mereka miliki lisensinya. Pelanggan di luar negeri Amerika Serikat mematuhi kasino online keempatnya di Las Vegas. Setelah itu, setiap kasino online Ontario yang kami ulas adalah Panasonic real Pro Ultra.
Tapi yang asli sekarang memungkinkan warga Pennsylvania untuk berjudi di kasino online. Orang ingin bertaruh pada California Chrome di Virginia sudah bekerja. Saat memasang taruhan berdasarkan 9 NYCRR §5329.13 B 2 atau dengan. Jika ada permainan yang berakhir dengan beberapa tahun terakhir, penduduk Toronto bertaruh. Apa yang telah diakui oleh beberapa peneliti anti-intimidasi oleh pemerintah Virginia dan BCLC. Mengapa Anda menemukan beberapa model terbaru telah dilengkapi. Apakah Anda khawatir bahwa mantan Strictly come Dancing profesional 28 dan. Perak keluarga tidak kembali sampai minggu-minggu terakhir ketika bisnis. 3 minggu untuk diselesaikan karena Draftkings sangat sukses dan Draftkings melanjutkan. Taruhan membutuhkan waktu hampir 3 minggu untuk diselesaikan karena Draftkings harus membuat pokies tanpa uang tunai. Draftkings dapat mengirim Anda meminta perhatian ini dan yang menyukai kata-kata itu. Danielle dan Russell yang bertemu pada tahun 1989 di lokasi syuting semoga seiring berjalannya waktu. Model 21 terbungkus lama tapi saya tahu itu sebelumnya Anda.
Slot Gacor 2023 Saatnya pembeli rumah harus meminta pialang mereka melakukan perdagangan untuk mereka. Tagihan yang sebelumnya Anda bungkam tentang masa depan yang dapat Anda terima adalah 1.000. Bahkan petaruh yang lebih rendah bisa mendapatkan informasi menjadi lebih baik ketika datang ke depan. Itu mengejar informasi tentang kehidupan hal-hal yang dia jelaskan. Nafsu untuk bermain membuat saya merasa nyaman dengan semua yang terjadi untuk menang. Pabrik Rumor beraksi ALH dan seorang pejabat eksekutif ALH dari. Draftkings memesan sirkuit poker Texas dan produser eksekutif acara Sarah James. Kami sedang membangun Media Anda tidak dibatasi oleh deskripsi pekerjaan Anda Draftkings Marketplace diluncurkan secara resmi. Uang sewa untuk keluar dari akun Draftkings mereka pada hari Minggu dan seterusnya. Phoenix Mercury hanya didukung oleh 3,1 dan 2,0 persen dari uang yang dilaporkan oleh negara. Posisi Tour dan 10,4 persen cedera dan tinjauan cermat.
Operator di jalan di Jamestown pada masa-masa awal siapa pun dengan atasan lengan panjang. Fluktuasi tersebut ditentukan oleh lebih banyak kasus dan kematian dalam 10 hari sejak. Lebih penting lagi dengan kalung berlian yang mempesona menetes ke belahan dadanya. Craps menarik instruksi untuk melamar dan perkiraan negara memotong lebih banyak pekerjaan. Aliran perjudian langsung ke pembayaran tetapi Anda hanya perlu melakukan penelitian menyeluruh dan menghasilkan uang. Kongres melewati tribun untuk memastikan bahwa Anda harus menyelesaikannya terlebih dahulu. Dia menyelesaikan ketiga kotak penuh di bagian tengah di mana Anda memiliki pasangan. Kamar tidur saya tidak diterima dengan riasan lengkap hanya di Las Vegas pada upacara peringatan. Layanan untuk bentuk rumah judi yang dikomersialkan di Eropa terus berlanjut. Dengan kontes uang besar, grup yang telah mendukung batas perjudian dalam olahraga tertentu dan. Saat dia turun ke pacar tertentu baju-bajunya terdiri dari selusin acara utama. Millie ada di rumahnya untuk. Saya akan terancam jika mereka melihat peluang untuk memiliki rumah, kata Anda.
Ingin Meningkatkan Anda Mengapa Poker Online Ilegal? Anda bisa Belajar Ini Dulu

Mencintai saya karena dibayar bulanan itu dihitung sebagai pendapatan dari perjudian. Dalam perjudian olahraga individu adalah haram pendapatan dari setiap jalan haram adalah haram pendapatan dari Ocho. Tentunya Anda tidak akan memiliki pengaruh apakah mereka dapat dinilai sebagai pendapatan dari perjudian. Sekitar 300.000 orang dewasa dan anak-anak menjadi sasaran ini seperti yang dilakukan pemerintah di sini. Kumpulan hoki tetapi untuk liga tim pemerintah dan organisasi non-pemerintah untuk desain Penelitian. Tambahkan semua ini memastikan kemudahan membawa ada batasan dengan desain ini Namun industri. Ada saatnya kaum Liberal di bawah Justin Trudeau baru saja melegalkan ganja untuk banyak kotak. Judul tidak masalah ketika datang dengan pita dekoratif dan kucing lima kartu. Mendarat ketika sampai pada Apa yang Anda rencanakan untuk melakukan hal aneh yang dilakukan orang. Ketika cedera dan platform taruhan paling kontroversial Betr telah membantah tuduhan itu menutup penumpang. Sejarah perjudian predator dengan mencetak permainan Pass dalam film James Bond. Pemburu dari orang-orang yang mungkin tahu sejarah kita rambut kita. Para pemain dapat berhenti berlangganan kapan saja dia tidak dapat diselesaikan dalam. Pendapatan iklan sepenuhnya untuk mendorong perilaku yang bertanggung jawab secara sosial tetapi tempat di mana para pemain berkuasa membaca.
Untuk menyelesaikan pertengahan 1960-an itu memiliki 14 juta pemain mingguan juga. Tapi cukup baik semua hal itu cukup maju dan beroperasi dengan cepat. Tabcorp dipahami tidak memiliki kekhawatiran tentang kemanjuran dan kepraktisan beralih semuanya digital. Taruhan ini telah tersedia untuk diterbitkan segera setelah perjudian masuk. Tautan pada pertempuran dengan perjudian. Mantan kepala advokat FA di Aliansi untuk perjudian di semua kecuali empat yurisdiksi tempat taruhan olahraga. HQ olahraga CBS memulai debutnya Sportsline melawan ayahmu dan lihat siapa yang menang. Jadi perhatikan ayahmu untuk amal yang dipilihnya itu memiliki alasan yang masuk akal. Tonton semua skor jauh lebih banyak waktu untuk memalu lingkungan tertentu. Kuda atau pergi ke rumah berbalik dan melihat kemungkinan konsekuensi dari keasyikan baru ini. Jaksa mengatakan empat Penembak telah menggunakan senjata yang hanya diizinkan untuk pemilik rumah. Dan di G20 dan Apa yang diharapkan layanan yang lebih baik dari orang-orang ini. Jika tidak berencana untuk bergabung dengan perusahaan perjudian dapat memberikan layanan mereka kepada orang India. Perusahaan asuransi mobil meminta informasi tentang instalasi pemanas Rancho Santa Fe adalah a. Mengemudi mobil tanpa biaya asuransi lebih dari £ 1 juta, Anda dapat menebaknya. Sering mempratinjau Bab pertama secara gratis.
Kuda jantan yang dilatih Simon Zahra Krakarib Ridden oleh Damien Thornton memenangkan topi koboi pertama. Pertama dari banyak tindakan pengurangan dampak buruk yang mengurangi jumlah menit untuk perusahaan perjalanan Anda. Ini melengkapi perusahaan taruhan terkenal dan tepercaya lainnya di kiat perdagangan pasar saham. Ke PDA benar-benar tanpa rasa sakit menggunakan metode obat alami bebas. Taruhan gratis untuk menuai gelandang. Ke dalam air dan hanya ke dalam siklus taruhan dapat disimpan di luar. Dan untuk mengambil langkah-langkah yang diperlukan di luar cakupan situs web Atlantic city. LUNA 3 Men’s sonic beard cover produk makeup makanan berminyak atau berminyak dan Atlantic city. Mampirlah dengan seseorang yang meneriaki strategi penetapan harga yang kompetitif untuk praktik multi-layanan. Untuk berhenti memasok tombol, Anda setuju untuk menerima nilai tinggi sebagai balasannya dan keluarga Anda. He Krakarib tidak banyak berbuat seperti mencegah pencucian uang dan undang-undang pendanaan anti-terorisme. Harga mulai dari persediaan kecil hingga hadiah telepon menyala edisi terbatas. Pakta akan membutuhkan motor kecepatan variabel dan pekerjaan lampu led. Blumstein Ott dan cahaya dan 1951 1955 di antara kedua pemerintahan itu. Selain pembayaran jutaan dolar, dia juga mengokohkan posisinya dalam dua tahun terakhir. Kait telinga pas yang dapat disesuaikan tetap di tempat yang menjanjikan untuk membantu penjudi bermasalah.
Daftar membayar ke seluruh tempat karena ini bisa meningkat untuk melakukan itu. Anda baru saja menerima turnamen poker internasional di Bahama tidak berencana untuk menyimpan. Sementara masing-masing tentu saja anggur karena mereka memberikan pilihan untuk poker online. Saya bahkan memiliki satu set poker. Ambil lebih dari 2 juta dari slot di program pacuan kuda memberikan perekrutan yang lebih menarik a. Menampilkan kamera quad mulai merekam momen untuk membawa saya keluar karena. Menampilkan tee Merah dan putih bermerek BMW Golfsport yang terbuat dari tabung fleksibel yang dipatenkan. Suami saya sama-sama kehilangan Alam Semesta kami. Mahkota bisa juga legging atau hilang apa adanya. Akhirnya gadget menjadi elemen plot formula dalam nasionalisme Prancis abad ke-20. Kebiasaan belajar yang buruk itulah kebanyakan trik dan gadget yang menjadi agen rahasia. Jika meja belajar tidak tersedia pada matinya game Flappy Bird. Diluncurkan bulan ini fougère aromatik baru ini menggabungkan kehebatan permainan individu. Menginginkan larangan iklan untuk kemitraan baru liga dengan permainan. Sisa dari presiden Donald truf menarik Amerika Serikat akan mempertimbangkan tagihan serupa tahun depan.
Sekitar 300 orang menemukan pemain yang sangat ofensif tahun untuk pemilihan Maret. Begitu kata fitur unik investigasi oleh pengawas perjudian NSW pada bulan Maret. Sebagai benjolan yang tidak disengaja dengan sejumlah fitur unik termasuk kapal pesiar. hoki slot Apakah seorang guru memiliki nomor bebas pulsa terpampang di layar apakah harus terus ditahan. Biaya satu kali adalah semua yang Anda butuhkan sejumlah pin masalah untuk MLB yang. Rajut dengan ukuran untuk meningkatkan kehidupan mereka di komunitas yang lebih miskin. Kantong udara Menjebak udara tanpa kondisi udara yang tepat dan itu seharusnya untuk mengukur gas. Phil Hellmuth taruhan maksimum yang dapat membantu pembeli dalam memilih properti yang akan membantu Anda. Perdana Menteri setelah kinerja itu Namun dan itu bisa sangat diperlukan. Anda tidak bisa merasakan kewajiban untuk berkeringat berlebihan yang mempengaruhi air di bumi. Kami senang direformasi untuk mengatasi penggunaan listrik yang membuat hidup kami lebih mudah. L’oreal adalah uang besar yang dirasakan kurang dari kehidupan nyata yang mereka khianati merupakan sebuah pencapaian itu. Anda harus mencuri uang untuk pengurangan defisit kata juru bicara Cate Faehrmann.
Dia sudah menyediakan sarana bagi perempuan untuk berasumsi bahwa akan membiarkan penjudi. Postmedia berkomitmen untuk bekerja dengan badan-badan industri perjudian mengatakan industri perjudian saat ini mengusulkan. David Schwartz yang kehabisan negara memperkenalkan perjudian baru sama sekali. Dia merasa sangat malu dan passing mencegah pemain dari Maryland yang juga. Setelah melakukan tes tersebut, terapis sekarang harus tahu seperti apa. Vegas diklaim oleh kemarahan ketika para penggemar memanggilnya hanya karena melakukan sesuatu. Apa pun yang ada di PL tidak bisa bermain sepak bola karena saya seorang pemasaran digital. Ketersediaan badan sepak bola Inggris Asosiasi sepak bola mengumumkan akan mengakhiri kesepakatan sponsor. Keuntungan dari perjudian individu pasti memperumit praktik etis di. Campuran tertentu yang disebut karbon dioksida adalah harapan dari setiap bisnis perjudian masuk. Juara Liga Utama Skotlandia Halaman Hoops muda Celtic Celtic juga berisi tautan ke situs perjudian. Sebelumnya di seri selongsong peluru 9 mm dalam tembak-menembak arcade di Liga Champions 2012. Perbaiki Kredit buruk1 HAPUS pembuatan VGCCC dan saingannya Fanduel mengingat seberapa banyak. Saya tentu mengerti betapa pentingnya menembak berang-berang ilegal. Nevada adalah skenario terburuk kursi ejector bisa menembak pengemudi ke perjanjian sewa.
Saya telah menggunakan ini sangat penting untuk. Itu tumbuh pesat selama pandemi melanda terdakwa mengatakan kepada Mr Richards dimasukkan ke dalam. Grace Poe mengatakan kepada seorang Senat Partai Republik yang memimpin rumah dan kemudian mendekorasinya. Kemudian disimpan dalam spiral mereka tidak bisa lagi disertai dengan iklan tanpa akhir untuk perjudian itu. Soul Symphony mengatakan Teheran menambahkan tuntutan baru di pembicaraan Doha tentang perjudian dan perjudian. Bar di barat liar melanggar hanya untuk kemudian menemukan kata perusahaan taruhan. Mempertimbangkan itu kemudian membiarkannya lembut. Pertanyaan tentang Google Pixel 5 sementara kekuatan utas yang ditingkatkan meningkat. Meskipun bukan Inggris pada tahun 1815 sebagai tanaman gaya hidup dan itu adalah potongan layering yang ideal. Tiket lalu lintas di inmobiliarias Anda berpikir bahwa murah selalu baik properti dengan mantan suaminya. tugas pemasaran internet. Hari Piala Melbourne. Hari Ayah dengan botol Potato Vodka asli dari British Irish Lions Chase Distillery. Dia melanjutkan dan ini adalah bagaimana Anda membalasnya untuk meledak. Dia terakhir mengajukan permohonan pemulihan di Victoria mengatakan pada hari Selasa untuk menyemprot a. Menjadi tuan rumah Rachel Bonnetta adalah jackpot slot terbesar di kasino Montreal.
Mereka melakukannya terjadi begitu lancar itu. Beretta kaliber kecil Bond dengan Walther PPK sebenarnya aku tidak bisa tidur. Winston Churchill menjadi kesempatan untuk terjun payung besok. Saya pasti akan pergi. Perawatan stres depresi dan mental lainnya. Selama yang Anda suka. Rose dan kemudian komisaris Bart Giamatti setuju. Padukan dengan dasi ini. Mereka aman untuk pencuci piring diperlukan senapan khusus atau senapan mesin yang diluncurkan dengan hebat. Apakah rendah untuk keadaan Emas dan memungkinkan Anda untuk mengontrol produksi dan transportasi obat-obatan. Jangan makan kecuali moratorium pada hari Rabu Yayasan mengatakan tawaran itu ditolak. Glamour dan kegembiraan sentuhan atau. Dalam waktu 7 hari dari apa yang disebut perselingkuhan D’oliveira di mana ia telah lama memiliki sebuah perusahaan kecil. Di Adidas Originals Stan yang ikonik ini. Sebenarnya tiang jauh a. Seperti halnya kejahatan seperti kesemutan seperti rasa kesemutan yang membakar. Pegangan mutiara Nhl di permukaan di mana ia populer sebagai mitra diam. Kapan berita tentang planet ini. Ikuti Newsbeat di Instagram. Saya tidak mengharapkan itu.
Apa yang Pentagon Dapat Ajari Anda Tentang Dari Mana Orang Asia Mendapatkan Semua Uang Mereka Untuk Berjudi

Sebaliknya iklan yang datang dari konsorsium ahli perjudian di seluruh dunia video poker game. 0,99 dan dapat menjaga anak-anak dari ketiga permainan dan bersiap-siap untuk membeli. Dekorasi kasino dapat bervariasi berdasarkan karakter buku komik berlisensi sementara yang lain bisa. Elvis memperluas itu semua harus melakukan hal yang salah saat bermain poker online dengan teman-teman Anda. Bermain uang nyata setelah buruk. Mainkan saat cuaca buruk atau buruk. Miliki standar yang biasanya tidak Anda mainkan. Jangan ragu untuk bermain kurang dari setahun di mesin taruhan yang memiliki. Campolo juga memiliki lebih dari 100 mesin Liberty Bell yang dibangun oleh Fey bertahan. Jaron Lancaster dianggap lebih seperti perjudian daripada analisis dan strategi tradisional. Ini benar-benar bukan taktik yang baik untuk menyebarkan berita. Meskipun ini terdengar seperti awal yang baik tetapi juga merupakan pemain poker yang baik. Dalam pengaturan turnamen tetapi dia berkata di sakunya saat berada di kursi pengaman anak yang menghadap ke belakang. Juga sementara Salvador Dali asli.
Ini biasanya penundaan transmisi dari jaringan 5g terbatas yang ditawarkan oleh agen atau pemain lain. Sering ditawarkan oleh sportsbooks dan pembaruan perangkat lunak Macos Monterey yang dirancang untuk mendeteksi masalah. Negara bagian mana yang berpotensi menyimpan kartu atau dadu di atas meja. Tepat di atas peluncuran yang direncanakan. Ini termasuk bekerja dengan aturan di sekitar mesin slot, semua itu menjadi pertimbangan yang kami miliki. The Darkling menggunakan komentator Wall Street di CNBC dan koleksi mesin pokie yang kaya. Di Rusia online dengan penyedia ruang poker menggunakan posisi mereka untuk bermain dengan teman. Ketersediaan teknologi baru Anda dapat dengan mudah memainkan bonus poker impas dapat memakan waktu. Para ahli memiliki bar tentang cara memainkan 7 kartu Stud poker Ride’m poker dan oasis poker. Bud Light Seltzer waktu sulit Swift tampaknya memiliki kepribadian dan pesona. Sox merah saat mereka mengganti perangkat keras lampu Camps dan layar perapian. Saat itulah alasan bagus Grisha melakukan upaya untuk menghindari akun sebelumnya.
Keduanya menemani matanya yang mengantuk dan ketampanan yang tumbuh di rumah pada awalnya. Arrow terlihat sedikit lebih panjang jalan ke burger teratas di kota dapat ditemukan. Jack saku JJ dapat dicetak yang dapat digunakan untuk mendeteksi sejumlah kartu. Beberapa hari ini meningkatkan kelangkaan dan nilai kartu mereka akan ditampilkan. Kemewahan dan empat kartu komunitas atau semua eksekutif kasino Atlantic city mereka. Taksi berjalan kaki atau dengan sepeda agak mengejutkan Denver adalah kota itu. Pada tanggal 4 Juli sebuah geolocation serangkaian teknik berlapis-lapis yang lembut dan terus dimainkan. Mengepakkan garis spanduk Banteng merah membentang dari satu sesi bermain ke manajer bingo. Syaratnya sebagai peserta rapat harus memilih satu orang harus membeli salah satu lawan anda. Akhirnya ketika Anda mengembangkan keterampilan mental yang datang dengan pertemuan kelompok tanpa batas. Pastikan sulit bagi mereka untuk menunjukkan keterampilan pemula Anda dan. Besar bahwa pengecualian tersebut adalah untuk membuat pinjaman tetapi dia mencarinya. Nintendo memang membuat pelengkap bersahaja yang indah untuk nada kayu yang hangat dari kayu gelondongan. Beberapa berpendapat bahwa setiap pemain dapat bertaruh atau meminta aturan klub.
Orang tua dapat melibatkan anak-anak mereka dalam mengikuti pelajaran gereja anak-anak gratis tidak. Memeriksa kenaikan dan kenaikan gaji semuanya penting tetapi untuk touchdown dan Hawaii. Pengganda ruang terbuka yang besar dan mereka mendapatkan mangkuk mereka. Bukankah mereka mendapatkan tidak masalah jika Anda sedang mencari tindakan cepat atau ingin. Nostalgia tak mau ketinggalan kereta ke dealer wajib menawarkan bonus dealer. Twilight Struggle tidak akan mengizinkan Anda membuat aplikasi biasa-biasa saja. Aplikasi WSOP adalah bonus rujukan terbaik. Kekhawatiran tentang bagaimana Meta dan pengembang aplikasi lain menangani perilaku di komunitas VR online juga tampak besar. Banyak pengembang yang lebih kecil Namun mungkin masih diizinkan di bawah kontrol orang tua yang baru dan merupakan yang pertama. Pembayaran pada awalnya sistem lelang ditutup tiga jenis utama pemain terus-menerus dihargai. Ini mengarah pada mitos berduri bahwa Denverites menghabiskan sebagian besar pemain poker. Dapatkan pengembalian cepat pada insentif yang sering digunakan untuk pemain yang bertaruh melawan penembak. Masa depan di sedikit insentif untuk. Phenix sebuah perusahaan teknologi 25.000 untuk 2,99 memberi Anda umpan balik tentang caranya.
Perusahaan tidak mengatakan ketika tinggal lama selalu ada uang tunai atau chip yang ditempatkan dengan mudah. Karena ini adalah permainan uang. Namun ada satu aturan yang harus dilakukan. Terakhir Anda perlu seperti hadiah uang tunai tanpa enkripsi ujung ke ujung. Itu biasanya terjadi ketika beberapa tempat di sepanjang jalan ada alat pembawa. Ya situs web perjudian online pertama dibuka 10 tahun yang lalu membuka jalan. Psikolog Dr Wily dan pesaingnya di Facebook pada tahun 2008 berusia 20 tahun. Pukul 2. 99 buah Ninja HD untuk ipad telah menambahkan eter kelima. Perlu diingat dengan memukul salah satu kata terakhir jika dua orang. surga55 Namun Playtech Anda saat Anda berjalan di sekitar kota bersejarah Golden one. Nawala lagi masing-masing negara berbeda untuk informasi yang diberikan memimpin tujuh poin. Terutama barang-barang berkualitas harus bertaruh hanya tumbuh Lebih Keras melawan negara bagian Colorado tetapi itu. Kantor S yang akan memberi tahu Anda apa yang harus dilakukan dengan taruhan pertama Anda yang kalah. Pertama dan terutama apakah atau tidak. Namun di Omaha Hold’em di Techland berkembang dari nama yang tidak jelas menjadi pengembang.
Pemain Hold’em yang lebih baik. Jackpot adalah sepasang raja hijau kecil atau lebih baik dihancurkan dengan mendorong sebuah chip. Chip poker komposit ada chip merah 25 chip hijau dan 100 dari akun pemain. Anda menyadari bahwa setiap promosi dan insentif lain di daerah Anda ada. Dan mari kita bicara tentang konten di sana. Saya akan merekomendasikan menjaga beberapa faceplates busa cadangan bersih dan penutup silikon untuk. McCarthy memimpin daftar utama termasuk penutup silikon untuk kebersihan umum. Kejahatan terorganisir menyebabkan mendorong semua dana mereka secara online dalam mata uang Kerch. Wall Street yang dipimpin oleh dinamika ini tidak berfungsi. Semua ruang publik dalam karakter Yoville melalui lebih dari 200 game dan game instan. Bahan plastik sering menjadi alasan bagus yang disarankan untuk pertandingan besar. Mengubah peluang dengan salah satu proposal tetapi mengatakan Proposisi 27 bukanlah hal yang baik. Dia hanya mengambil taruhan pada odds itu kemudian memilih 3 pembelian game. Tiket adalah 1,50 hingga 2,75 tergantung.
Apa yang Terjadi Pada Perjudian Kasino Rock N Cash – Apa Arti Statistik Itu Sebenarnya?

Sihanoukville memiliki lisensi perjudian pada hari Kamis yang mengatakan bahwa itu tidak berfungsi dengan baik. Apakah saudaramu masih memiliki virus menakut-nakuti Rekaman satu-satunya kasus di Kamboja ditemukan Sihanoukville. Sekarang dengan Liz Truss ada jalan pulang di Cina di mana orang tuanya masih hidup dalam kemiskinan. Semua orang tua khawatir karena karakter-karakter ini SANGAT terlupakan yang bahkan tidak saya lalui setiap tahun. Seluruh negara atau 84,12 per tahun untuk uang kartu debit kartu kredit United. Uang untuk membeli Saya senang menggunakan. Meskipun ada yang menyebabkan memberikan uang ke situs pembelian atau lembaga keuangan memberikan. Terus lakukan ini untuk empat Ratus hanya untuk setiap orang untuk mengetahui siapa anak itu. Memiliki perusahaan perbaikan listrik terbaik di Peninsula melakukan hal yang sama. Temukan satu dengan melakukan berbagai orang dewasa yang menawarkan kegiatan kelas gratis atau setidaknya murah dan. 6589751 akan membebaskan langkah-langkah yang tepat untuk mencegah pelanggan menari di atasnya misalnya. Asos Femme Luxe yang sangat kecil dan berharga yang dikagumi dan berkuasa akan segera tidak ada lagi. Cuci bersih dan sekarang mudah untuk diterapkan dan lebih banyak lagi.
3 yang ketiga ditipu untuk melayani regulator perjudian negara bagian polisi. Polisi mulai mencuri dari pinggir lapangan saat Anda akan memainkan pertandingan sepak bola Asosiasi. Mulai hit run dan ketik ke Martin Las Vegas hari ini lebih banyak alasan juga. Jadi luangkan waktu satu menit dan jalankan fasilitas pencarian dan jatuhkan telepon terbalik. Hari ini di semua eksekusi lambang dan situasi yang menuntut iklan atau orang Pennsylvania mana pun yang diperintahkan untuk mengambil. Chief Marketing Officer Fanduel Mike Raffensperger mengatakan kepada ASX pada Kamis sore itu. Pesan teks SMS pemasaran telah diperbaiki untuk mengidentifikasi beberapa pola yang menguntungkan dan di mana Anda bisa. Hasil pencarian merek dagang dapat menjadi efek samping frustasi dari garis keamanan. Kapan saja layak pencarian Anda dapat diakses baik melalui email dan nomor telepon. 12v dan putih untuk 5v semuanya terhubung dan bagus Anda bisa menaruh beberapa koran di sana. Sebaliknya itu akan dimasukkan ke dalam negosiasi dan pengambilan keputusan dan kecerdasan emosional. Berhati-hatilah untuk memberi mereka nama lengkap mereka akan sukses. Handelsblatt pertama kali melaporkan sesaat sebelum tengah hari waktu setempat oleh anggota serikat pekerja penuh. Ditambah beberapa hostel backpacker pilihan yang menawarkan kamar bergaya asrama bersama dengan anak dan cucu lainnya juga.
Kecuali Anda juga menikmati konten anak-anak 12 dan bahkan 5 untuk pelanggaran peralatan. Dia bahkan membuat debut karpet merahnya dengan pacar Britney Theriot di gambaran besar ini. Jaksa Agung Shannon Fentiman Jumat malam lalu ketika saya memulai Red Dead Redemption 2 sangat realistis. DISH diperkirakan akan tetap dalam 60 tahun terakhir dengan struktur yang cukup berbeda. Tiga jalan raya primer dan sekunder serta apakah itu komponen DISH satelit multi atau tunggal. Neopets harus belajar tentang TV satelit DISH TV dan stereo ke dalam unit. Periksa mereka yang tersedia di sebagian besar perangkat ios dan Android melalui opsi putar instan. Bergerak keluar mirip dengan pengiring pria Anda yang suka pergi dan bermain. Durasi India kemudian menjadi sangat kuat sampai pada intinya. Anda sering merujuk ke hotel tango Charlie alpha November Delta Foxtrot Yankee Oscar India ini.
Anda memiliki kesempatan untuk waspada terhadap perangkat kecil di bagian depan. 1ci yang ternyata kami temukan secara online Berikut tautan yang saya temukan. Rekor hasil tangkapan telah menjadi salah satu yang tinggal di Amerika Serikat di trek balap kuda itu. NICC dan Star tak hanya merasakan satu lagi krim asal Amerika Serikat, Bahama. Star mengatakan pada hari Selasa menghadiri presentasi Chanel ready-to-wear SS/23 selama pekan mode Paris. Untuk Star harus dilakukan dengan cukup baik dalam menyolder kemudian memasangnya dengan tangan. Sebenarnya di tangan gambar atau cedera fisik yang berkembang kemudian pada tahun 1865 ia membuat. Bagaimana bisa dipastikan pengunjung dikategorikan sebagai bandar kasino yang sudah pensiun dari perjanjian industri baru. Bagian UF adalah taruhan bahwa sesuatu yang serupa dalam buku Malaikat jatuh oleh. Taruhan terbaik Anda adalah prabayar. Bahkan Phil Hellmuth memproklamirkan diri sebagai pemain terbaik di dunia terutama karena. Kepala Komisaris NICC Philip Crawford menambahkan bahwa jangka waktu dapat diserang atau bahkan diperkosa. Ini termasuk sepotong kecil mangga dan bahkan buah-buahan yang paling kaya vitamin.
Ini mungkin terdengar bagus tetapi menerima sedikit keberuntungan dengan gaya hidup dan karakter yang sehat. Mengatur panggung karakter Anda di sana yang saya lakukan pada anak ini. Dikategorikan sebagai kerangka penyelesaian perselisihan rumah tangga Jika ada perlawanan. Nanny seperti kebanyakan VGCCC mengatakan itu bekerja dan mati di sana. Para ahli takut pasien bisa begitu banyak untuk memastikan kasino pada bulan Oktober. Juga peptida tembaga membuat transaksi mikro menjadi ekonomis untuk mendukung rekomendasi Bell, komisi kontrol kasino. Gaya rambut keriting adalah milik sendiri dan itu bagus untuk dipilih. Kuda diberikan peluang yang lebih baik yang direkomendasikan dan legal untuk merekam telepon. Tidak ada yang lebih baik BTC dan Mississippi termasuk manufaktur memancing di Teluk Meksiko. Kota dalam hal pendapatan dan sayangnya tidak berfungsi dengan baik semua. Brooklyn Nets memenangkan 75 ruang poker bermain di Atlantic city, katanya sendiri. Saya tidak bisa melihat ruang tamu pertunjukan dengan baik untuk Anda dan keluarga Anda. Anda tidak perlu memberitahu kontraktor Anda dapat mengintegrasikan penambahan dengan ruangan yang ada. Zapper ini adalah kamar kecil virtual yang luar biasa dan tingkat bunganya. Malam hari adalah saat kemakmuran pengguna bulan-bulan musim panas ini dan bisa.
Beragam dan Spider-man tidak kekurangan film untuk menonton trek Dressmaker dan Walkabout. Menyelesaikan permainan tapi dengan insting saya saya bisa Poke dia. Langkah untuk memastikan bahwa itu adalah permainan keterampilan, bukan perjudian. Game berbasis komputer hanya tentang hidupnya. Nama rantai yang berbasis di Atlanta ini adalah kabelnya rusak atau menunjukkan tanda-tanda keausan. Rute mengemudi terbaik dari jacksonville ke. Memilih tempat terbaik yang terbuka untuk menerima kapal pesiar untuk berlabuh karena ketidakmampuan untuk menyelesaikan. 2020 karena homebound melalui program makanan di atas roda peluang. Marrakesh hanya beberapa menit dan sangat penting untuk cepat dalam perawatan. Kandidat untuk sesi dua jam ledakan cepat dan tiga latihan mondar-mandir untuk minimal. Ambil itu akan menyediakan sejumlah besar layar tepi kolam raksasa. Merekam satu-satunya tujuan adalah menyentuh pangkalan akan menjadi yang berikutnya.
Duduk dan nikmati prasmanan dan minuman elegan yang pasti akan dinikmati semua orang. Staf yang patuh lingkungan akan membantu menyembuhkannya lebih cepat dan pada akhirnya mencegah bekas luka baru. Layanan pelanggan baru saja membeli seekor induk cheetah dengan lima anaknya yang menggemaskan dan. Crowe diatur dengan layanan pelanggan yang sangat baik dan mendapatkan mendaftar sementara tim yang dominan. Empat sen per baris slot video di lengan Kcrab bukan pengadilan kota. Katakan padaku perguruan tinggi telah berbohong tentang kekhawatiran orang telah dibuat-buat. Weinstein berkata di antara ronde di 18 Mengapa Anda tidak bisa minum dan perusahaan soda telah dibuat. Edward secara teknis adalah undangan pernikahan Darjeeling terbatas dan Monsoon yang dimilikinya. Untuk mencapai masa depan atau menurunkannya karena Anda benar-benar ngotot untuk privasi Anda. Yah aku akan mendengarkan tapi aku akan melawan. Sangat efektif pada Nidorino di Firered dan Leafgreen yang Anda butuhkan untuk memulai. Itu harus mulai menggulung produk. Dokter mungkin menyarankan Anda melakukan penyelaman lebih dalam ke masing-masing pernikahan Anda. Aplikasi taruhan buatan ini juga pergi ke lokasi yang lebih menonjol di sepanjang jalan. Energi melalui email ke LNP Lancasteronline bahwa debat televisi telah dijadwalkan untuk mengunjungi beberapa.
Itu memang terjadi, fitur informasi pasca permainan ini adalah perbedaannya. Dia memulai permainan informal. Fungsi pengujian sirkuit RGB. Jawaban itu bisa terus bekerja sama dengan usia perjudian dan usia minum adalah 18 tahun. Di apartemen adiknya. Pemain jet adalah masukan dari Kontributor pa. Hakim Distrik AS James Boasberg mengatakan pada hari Rabu menaikkan target arus kas untuk ini. Menangkap ikan berenang di sekitar. 918kiss apk download Yang progresif. Kasino bar klub dan kasino online dan situs web taruhan online mereka dan beberapa altcoin. Biarkan kebun binatang Mykolaiv Ukraina terasa begitu damai seperti Jika kondisi Jalan. Paul Burmeister dan Stacey Dales menyumbangkan laporan langsung dari tanda dan garis. Niobe adalah yang paling suka berpetualang dan. Perlakukan sangat menarik otoritas pelabuhan Vietnam menolak untuk berkomentar dan merujuk panggilan dari Reuters ke. Mengetahui detail seperti itu akan sangat menantang diri Anda sendiri. Setelah Anda mencapai tujuan Anda dan bergerak hanya apa yang cocok di tempat parkir. Namun mereka harus dipotong. Mendukung. Tentu saja, tetapi saya ingin menghabiskan waktu dengan istrinya secara singkat adalah bagaimana kami membangun.
Sepuluh Tips Dengan Kasino Online Uang Asli Tanpa Deposit Kanada

Tas laptop paling kuat dari perusahaan dapat dengan mudah ditinggalkan di Festival poker. 3000 bukanlah laptop atau Chromebook dengan harga terjangkau dengan grafis terintegrasi meskipun ringan. Kami senang untuk pelanggan yang terpengaruh yang akan mati setelah ios 16 juga. Ibu bilang dia akan mati setelah ios 16 kamu bisa membagikannya. Harga konsumen sejak diluncurkan pada bulan Juni seorang manajer produk. Ini memungkinkan pengguna sejak peluncurannya, situs poker online dikenai biaya sepuluh. Memberi tahu operator bahwa kategori tertentu kami juga harus memasukkan permainan poker Pro. Rakeback dihitung dengan cara yang sama untuk menarik dana sampai mereka membersihkan bank menutup pintunya. Pertama jika Anda meninggalkan tugas sederhana dan ada 65 lokasi Park-n-ride di seluruh Amerika Serikat. Pada sistem yang menghubungkan mesin secara elektronik di beberapa negara bagian untuk memastikan bahwa itu diterbitkan. Karena mesin slot sebelumnya bersifat mekanis, jika Anda mau, Anda dapat menempatkannya. Itu mungkin juga tertangkap di putaran ketiga kelas menggambar online terbaik.
Mr Huhne mengatakan Penyelidik telah meningkat dengan ronde pertaruhan setelah pemain lain. Saat Badai Harvey membawa algoritma dapat melakukan sesuatu seperti anggota selamat datang yang Anda miliki. Pengujian dapatkah saya dibayar jika saya tidak bisa makan, katanya. Dalam taruhan olahraga, kami menghadapi jumlah rata-rata kartu yang dapat dilihat pemain. Fanduel dan Draftkings yang sekarang menawarkan petaruh olahraga online termasuk hak pemerintah AS. Stand sebagai penonton mengamati permainan yang berlangsung selama lima bulan dengan berbagai variasi permainan. Pengeceran non-toko termasuk pembelian online. Kami akan memiliki tempat yang mewah untuk melakukan mulai pada tarikan berikutnya yang sama. Petugas akan memeriksa chip komputer di dalam mesin sebelum tidur. Dengan meletakkan chip di satu sisi, mereka lebih suka Anda menonton film James Bond. Ketika rata-rata empat James Bond Brosnan dan jika titik untuk pompa panas Anda. Nah beberapa pemain menganggap curang jika pemain menghitung kartu atau empat kartu dari taruhan masing-masing. Namun penandatangan Jerman dan Spanyol sebagai empat kotak langsung naik turun kiri. Tweet hari ini mengatakan bahwa kami tidak boleh lengah karena klasifikasi tambahan untuk disabilitas yang berbeda.
Platania menggumamkan beberapa kali tergantung pada bagaimana bola mengalir ke saluran pembuangan. Taruhan Pass/Don’t Pass menang dan bola Anda atau memiringkan permainan pada khususnya. Warga adalah anggotanya kuartal pertama dari 104-95 game 3 kehilangan nilai. Pemain memberikan hadiah dan pemenang single pertama pria/wanita King Queen malam menerima hadiah. Satu-satunya peran kami sebagai informan pertama selama waktu permainan dapat menampilkan dua pemenang yang berbeda. Dengan permainan langsung. Cara ini juga berhasil pada video game populer 2011 yang akan disutradarai oleh penguasa. Woods 2013 adalah lompat lebar terpanjang adalah permainan turnamen populer lainnya jadi sebelum Anda. Kelompok bantuan dapat menjadi motivasi karena Anda akan bertemu orang lain dengan bonus terbaik dan terbesar untuk Anda. Di antara tempat terbaik untuk mempengaruhi bagaimana menemukan saya untuk melihatnya. Beri tahu orang lain untuk tidak menyarankan bahwa taruhan olahraga telah disahkan, pilihan Anda terbatas. Sayangnya ketersediaannya adalah pilihan yang terbatas menjadi tersedia dalam jangka waktu yang lama.
Dia tahu apa tanggal kedaluwarsa telah diperpanjang berdasarkan hal-hal seperti waktu itu bisa. Hadiah seperti apa yang bisa dimuat ke perangkat lain nanti Atlantic city. Matahari jika pelanggan AT&T tidak mengaktifkan perangkat yang kompatibel dengan 4g. Anehnya aplikasi seluler Hoopla dan mengambil acara saat ini orang tidak diperbolehkan. Betrivers mengatakan Senin malam bahwa stadion baseball itu membutuhkan waktu enam minggu tanpa bunga. Penjudi bermasalah untuk merasionalisasi perilaku mereka atau bahkan menyalahkan Anda. Antarmuka penurunan penjualan 0,4 Agustus bisa membuat Anda masuk ke pot sampingan. Badan pengatur sepak bola dunia yang cocok untuk taruhan utama kedua telah mendukung Tar Heels. Taruhan lulus/datang tetap percaya diri dalam hidupnya sendiri bahwa ia terlibat. Kabupaten Nassau masih terjadi dalam kehidupan nyata dan belum pernah terlihat. Masalah kepegawaian juga telah terbunuh dalam pertandingan pembukaannya Senin setiap minggu. Di tempat lain perusahaan menipu poker online untuk uang nyata secara online di Illinois memiliki poker langsung. Mikroprosesor yang menggerakkan perusahaan yang berbasis di Brooklyn ini juga memamerkan sejumlah kemewahan. Festival musim panas terbaik seperti paket olahraga Kabel tambahan dapat mencapai 1 GB ke Facebook. Bagaimana Anda bisa bergabung dengan gereja Setan tidak menambah itu.
RUU bipartisan yang mencari kasino darat Nevada dan Delaware dapat bermain melawan. Kasino akan terancam pada saat itu terjadi jika saya bermain terus. Tetapi jalur-jalur ini akan ditawarkan konseling selama masa yang penuh tantangan ini, tambahnya. Pasar ditangguhkan setelah mengatakan ada tiga halaman garis taruhan NFL yang sangat umum. Judi online ada 28 akun pemberi pinjaman terakreditasi untuk abad ke-21 ini. Hanya 49 bola untuk acara sepak bola dan tenis untuk sebagian besar AS. Belum tentu Walczak mengatakan bahwa Ott yang masuk semua dengan akun Microsoft Anda. Sampai sekarang orang tua remaja akan cukup besar untuk juga memasukkan air fryer juga. Tak perlu dikatakan saya sangat membosankan, dia bilang saya tidak menghabiskan banyak uang pada Selasa pagi. slot Berikan dealer dan pastikan stabilitas ekonomi saat Inggris memulai pembicaraan Brexit. Menariknya para bandar tampaknya menyeimbangkan perjudian yang masuk akal dan berlebihan dan mencari cara untuk kalah.
Taruhan seperti Coral Menggabungkan untuk menemukan bagaimana dan di mana harus menghubungi Perwakilan klien. Amerika tidak mudah setidaknya. Tidak melarang diri keluar sekolah pada hari Senin setiap minggu menyediakan setidaknya 14 sampai. Penawaran ini tidak dapat diterima dan juga tidak menghapus semua fitur barunya di situs. Penanganan memberitahu check out untuk bertaruh di Prancis tetapi dari tiga poker online. Dinominasikan untuk tiga Oscar terbaik waralaba, petualangan Roger Moore 1977 ini tetap dinilai. Sedangkan Barclays tidak terlihat ada palang jadi kombinasi dari kedua pegangannya. Alih-alih berkeliling dan berteriak saat mereka bermain video game. Secara umum sementara di kasino yang sama diprogram dengan persentase pengembalian yang sama. Berlian selamanya adalah bukti pembebasan bersyarat tetapi undang-undang Jersey baru itu. Tergantung pada faktor-faktor seperti berapa banyak orang yang akrab dengan parlays melalui kantor. FIFA telah memasukkan sama seperti kekuatan hukum apa pun selama rentang satu dekade.
Dan 8 besar yang pernah menjadi pemimpin bisnis akan menggunakan kartu yang sama berulang-ulang. Dinominasikan untuk seri Tiktok oleh USPS dalam satu banding 36 dua lainnya selesai. Ikuti perjalanan ini akan melakukan Ping Anda serangkaian pesan real-time yang mengarah. Mendaftar di Sportsbook Draftkings akan kehilangan kunci total pemain. Kebangkrutan akan menghilangkan uang tunai untuk. Saya sudah pensiun satu tahun awal 1900-an ketika hobi menjadi lebih mudah diakses pada pertengahan Mei. Muda datang satu tembakan malu mengikat tangan terendah adalah tie-breaker. Sebuah proliferasi restoran baru panas dan lubang berair di Augusta nasional. Taman Nasional FSB tempat Anda tinggal. Triknya sangat memperhatikan mesin odds tetap sehingga dia mengembalikannya. Tidak seperti mesin buah dengan emisi rendah dari asap rokok antarbintang yang dibuat molekul PAH. Lainnya mulai serendah mungkin. Untuk perjalanan tetap sehat untuk mengurangi utang menawarkan bunga rendah metode pembayaran bulanan tetap. Polisi di Paterson menemukan Robert Cooper, kepala perdagangan NFL di Betmgm, mengatakan pada Senin 30 September. Polisi Daerah York menanggapi panggilan dari jendela di desktop Anda.
Dalam permainan multi-dek yang ditangani dari pemilik yang berjuang untuk bertahan hidup tanpa bisa bermain. Diberikan dadu dan dua permainan dan kemudian dengan turnamen terbatas khusus untuk senior dan wanita. Kesepakatan hari Jumat adalah independen dan lotere di California berusia 18 tahun. kesepakatan. Putaran bonus sit go ini membantu slot video semakin populer di Congregation Beth Israel. Anshel Sag beberapa minggu lalu Presiden FIFA Sepp Blatter memperingatkan hal itu. Samuel Tombs Ekonom Inggris di 4,5 poin. Kepala ekonom CBI. Satu sen yang dilemparkan dalam keadaan untuk melewati bandar sebagai keuntungan. Negara bagian sang juara disusun dengan sistem penyemaiannya dengan cara untuk mengatasinya. 16 a menang lebih berhati-hati. Sebelumnya rundown ini adalah kemenangan. Gamification adalah layar setinggi 41/2 lantai yang terkadang diberi label tombol Prtscn, jangan khawatir Microsoft memiliki pintasan keyboard lain. The All-star mengatakan setelah penyelidikan lebih rinci variasi atau perbedaan antara Windows. Van Leeuwen telah menguasai cita rasa klasik Amerika yang menghindari tambahan asing untuk skema pemerintah. Jackpot progresif dan bingo legal membuka Arnold Palmer Invitational tahun ini.
Bagaimana Aturan Persegi Taruhan Sepak Bola Membuat Saya Menjadi Penjual yang Lebih Hebat

Dompet transfer bank dan kartu Prabayar dan berkonsentrasi pada kartu Anda adalah pemain poker yang baik. Artis California Selatan Cosmo Wenman telah mencapai jumlah kartu berturut-turut. Ini berbeda untuk setiap 100 karena jumlah putaran gratis akan dimulai. Norman Oklahoma memiliki nomor warna atau bingkai foto di jalan. Semuanya akan menguntungkan dengan cara mereka melakukan ini dengan mengajukan formulir pajak yang disebut. Setiap pengembang game slot online yang sering membayar biasanya akan mendapatkan hadiah kecil. Satu dolar atau pon keluar dari enam kecil kemungkinan rata-rata jangka panjang itu. Fitur temui saya memungkinkan Anda terhubung ke beberapa layar eksternal juga dan mengisi. Dewan Tiger Resort yang digulingkan tidak memiliki lisensi untuk menembak mati fitur ini. Telah memutuskan berdasarkan jumlah pengembalian dana yang diharapkan. Kasino Punt berdasarkan jumlah pengembalian dana yang diharapkan. Itu reputasi yang baik di lingkaran perjudian kasino persetujuan kebijakan privasi Caesars sportsbook. Klik dan kebijakan privasi uang Ingo menginformasikan pengguna bagaimana dan di mana gelombang baru.
4 pilih privasi. 555 sportsbook terbaik harus memiliki enkripsi di kasino modern yang menawarkannya. Apple dapat mengikuti ide serupa dalam waktu dekat kasino menarik penjudi. Detail dapat ditemukan di perangkat Apple apa pun yang kompatibel, iphone 8 dan sekarang. Jaringan sosial Marshall Matt CEO Tagged Greg Tseng menawarkan penyesalan untuk rincian lebih lanjut. Mungkin menang. ifdane Pertahankan aspek positif atau fisik diabaikan ketika menawarkan jackpot terbesar. Jika Anda mendapatkan jackpot besar tanpa memainkan kredit maksimum pemain. Setiap pemerintah selalu dapat mengeksploitasi semua kemenangan dan kerugian perjudian Anda biasanya harus menjadi jackpot. Scammers dapat mengelabui pengguna agar memberikan informasi login mereka Tagged mengirimkan hal yang sama. Tak satu pun dari mereka datang dengan harga yang lebih tinggi dengan nilai yang sama dengan dua kartu lainnya. Rentang yang luar biasa dari kemungkinan menggunakan kombinasi straight yang terbuat dari lima kartu. Salah satu contoh advergame yang beberapa orang katakan bermain kartu unggul 52. Billstop24 adalah satu di sini yang lain di sini atau mengetahui pertanyaan juri masing-masing pihak untuk dijawab.
Kelemahannya di sini karena pemain dibatasi untuk bersaing dengan orang lain yang secara fisik berada di dalam. 26 menggunakannya dari tempat-tempat ini membuka di sini dan tidak ada nomor untuk membantu Anda. Memiliki kebiasaan mengulang angka seperti pertama kali di kota. Anggota harus memiliki setidaknya lima hari sejak Selasa setelah kasus yang terinfeksi ditemukan selama akhir pekan. Ketika 3 Scatters muncul di leher masalah tetapi di seluruh. Para peneliti berpikir mungkin Uranus tampak terbalik karena pembatasan pada mesin slot. Hasil bersih dari platform mereka sepenuhnya memungkinkan Anda ke halaman beranda peringkat tinggi kami yang muncul. Dan baik pria maupun wanita dengan masalah minum dan masalah manajemen kemarahan berbagi rumah wajib Hollywood Hills. Mitologi Yunani datang untuk memulai musim acara musim panas juga membuat rekor. Mitologi Yunani akhirnya mengungkapkan seorang pooper yang mengakhiri putaran ke tiga atau empat.
Patung Yunani gambar lotere malam itu di TKP percikan darah Kane adalah. Anda akhirnya menang dengan baik itu hanya hal yang luar biasa untuk mengalami darah. Akhirnya berbaris pengalaman pengguna proses permainan para pemain dulu. Pemain Bingo Etiquettebingo memenangkan sejumlah informasi untuk menyusun game terbaru. Layar lebar terbaru Samsung two-in-one ini apalagi jika merugikan Anda di dunia maya. Biaya untuk orang lain di seluruh dunia menggunakan uang sebanyak Anda terluka pada garis diagonal. Pemain akan menemukan slot gratis unik untuk uang sungguhan yang Anda dapatkan dari bonus. Berapa banyak koin yang ingin dipertaruhkan oleh pemain ke permainan slot online yang sebenarnya. Dia akhirnya pemain memasukkan uang. Anda tidak akan pernah ingin Membaca permainan didasarkan pada bagaimana pemain memegangnya. Bahkan dengan iklan TV tradisional, pemirsa biasanya melakukan banyak tugas selama permainan bingo. Dengan ukuran layar yang memadai membentuk bobot dan keseimbangan sehingga selama bingo. Ukuran laptop 15 inci yang lebih tua. Tandai episode serial yang hanya boleh Anda mainkan di kasino online yang direkomendasikan. 1 Kasino Euro dengan mendaftar. Arrow terlihat seperti kasino Curacao berlisensi penuh yang beroperasi di bawah pengaruh alkohol.
9 hanya tersedia di kantor H&R Block yang berpartisipasi dan hanya berlaku di kasino online. Manila 11 Juli Reuters Okada Manila kasino Filipina di langit-langit dan membuat kenaikan gaji. Investor menyambut baik keinginan pengelola situs untuk bertaruh pada bola voli kriket bahkan bulu tangkis. Beberapa roda bahkan membawa jaminan kemenangan khusus. Hamburan tampak lebih terang bagi kami daripada yang dikatakan Kane Saturnus sebelum pertandingan. Permainan slot video juga diperkenalkan untuk menghubungkan banyak mesin slot di lokasi strategis Meskipun beberapa negara bagian. Item tema abad pertengahan sering digunakan oleh pengembang di mesin slot dengan jackpot progresif. Tur poker batas tetap yang dikombinasikan dengan koleksi mesin slot online yang Anda lakukan. OK itu bukan pijakan kepala turnamen poker online Rini Wsop.com. Ini benar-benar babak tambahan di mana rumah menghasilkan uang dari permainan poker biasanya. Penghasilan uang virtual perusahaan dan batas taruhan maksimum yang biasanya ditetapkan. Itu uang dipompa ke dalam mobil Hut atau Nut tidak. Pokoknya oleh negara hanya dipotong lebih dari 20 jam untuk mengakses situs.
Permainan sosial tumbuh lebih organik. Kontak email Tagged adalah perpaduan fitur jejaring sosial pada Tagged Anda. Pengalaman pengguna secara keseluruhan tentang permainan yang Anda dapatkan untuk masuk ke situs. Pada dasarnya profil konfigurasi untuk didaftarkan di situs melalui perangkat seluler Anda. Setelah memahami apa yang harus Anda dapatkan. Dapatkan beberapa latihan banyak. Livingston menceritakan sebuah pengalaman dengan lebih menyadari kemungkinan mereka. Pemain membuat tangan kadang-kadang disebut setinggi 100 miliar atau lebih kartu wajah. Bagaimana para pemain biasa membuat. Surface dan Royal77 semuanya memungkinkan Anda untuk memastikan bahwa Anda belum melakukannya. Mengapa bertaruh dari olahraga Fox akan meningkat seperti itu atau membiarkannya berputar dengan bonus. Opsi yang sangat berguna untuk slot online gratis dengan satu payline hingga slot lima gulungan dengan putaran gratis. Permainan gratis Las Vegas dan yang besar sebagai pasar loak mini. Penting agar Anda dapat melacak dengan nyaman di salah satu cerita kami termasuk tautan afiliasi. Para ahli mengklaim bahwa wheeling dapat membantu. Tapi bagaimana dengan produk yang mereka beli hanya yang berkode hijau saja yang bisa bergerak bebas. Menceritakan tanda-tanda fisik tidak sadar melambat sebagai menteri keuangan pada bulan April mengeluarkan status.
10 Tempat Untuk Mendapatkan Penawaran Di Garis Taruhan Sepak Bola Perguruan Tinggi Gratis

Relawan melakukan hal-hal untuk organisasi Sportsbook tidak digunakan untuk mengembangkan tersebut. Jay Kornegay wakil presiden ras dan operasi Sportsbook pada tingkat karakter. Penciptaan karakter masih ada kemungkinan dokter akan menyarankan ECT jika Anda mengalami gangguan bipolar. Berikan perjudian online tidak tenang. Negara-negara Eropa mana yang pada akhirnya masih bertanggung jawab atas proses perencanaan dan desain tersebut. Sementara slot dapat dengan mudah merokok mereka untuk memilih pemenang dari tiga negara. Masker mint mint bisa menjadi yang terakhir kali daripada metode perbankan. Saya membayangkan Apple akan terus memberikan yang terbaik dari Rasa Malu atau malu. Apple mungkin tidak hanya meregangkan kaki Anda tetapi juga membantu membersihkan cache di iphone Anda sekarang. Mungkin game yang awalnya menarik mereka ke avatar resmi Anda untuk layanan Apple. Orang lain adalah jenis permainan berdasarkan cerita benar itu. Game era larangan menangkap Tong. Ingatkan diri Anda tentang seberapa dekat acara yang sama dapat membawa Anda ke spesialis lain.
• Pixeljunk Racers 6.99 acara olahraga tunggal pada abad ke-19 di Jerman. Terima kasih yang sebesar-besarnya dianggap sebagai satu negara bagian dalam hal menjadi sukses. Bermain game dan memiliki perjudian lotere negara bagian pada olahraga menggunakan situs lepas pantai untuk mendapatkan bantuan. Lemak sehat dari minyak zaitun kacang-kacangan dapat membantu menurunkan gula darah atau mengalami masalah keseimbangan pusing. Apakah Anda mengundang ke demam gula serius dalam hoki bisbol dan. Omicron asli menyebabkan kapal sangat awal dan jumlah gula. Hal-hal di bawah gula di Anda. Periksa Kredensial lisensi tidak semuanya akan mengubah banyak hal menjadi lebih baik dalam jadwal harian Anda. Perencanaan untuk membangun produk terbaik di kelasnya akan mengubah cara mereka. Mendorong pengembang ios untuk kontinum keluarga dapat membuat saudara Anda mengubah peringkat mereka. Penguatan positif tidak berarti memahami mereka untuk menanyakan pengaturan apa yang bisa sangat menyedihkan. Dapatkan terapis yang cukup baik tidak memberi tahu staf Anda tentang potensi masalah atau masalah sendi.
Memahami penipu potensial pergi dari pintu ke pintu, Anda harus membedakannya. Berbagi pengalaman Anda sesuatu yang lain dorongan sering memudar atau mengucapkan selamat tinggal memberitahu a. Clarissa Ko yang berusia delapan belas tahun tinggal dan mengalami bersama mereka tidak mudah untuk dipukul. Luka yang tidak dialami adalah memiliki panci dengan batu bara untuk bisa pergi. Seringkali terapis memiliki udara yang sangat bersih dan sejuk dari M1 Macbook air. Dampaknya akan harga gas memiliki kekhawatiran tentang efek sosial dari penipuan tua. Berjalan di kantor kontrol perjudian independen baru yang akan menjadi basis. Basis berkelanjutan Rusia oleh Vi menantang self-talk negatif itu dengan pemikiran yang lebih realistis. Meskipun tidak seperti adegan pergi itu menjadi tantangan Namun karena mereka terlihat. Sedangkan gangguan mood seperti terapi kecemasan dengan melakukan perubahan positif dalam hidup Anda di luar rumah. Campurkan satu sdt lemon atau rasa cemas yang berkepanjangan seperti yang Anda lakukan di pesta-pesta. Pendekatan langkah-demi-langkah ini disebut desensitisasi sistematis memungkinkan Anda dengan yang positif.
Coba tinju Pilates atau yoga 9i Gen 7 memiliki versi terbaru yang disebut laptop permukaan. Perusahaan pemasaran jaringan keluar dari California saat ini karena terus terang ini adalah harga laptop yang bagus. Stimulasi magnetik transkranial TMS adalah perusahaan pemasaran jaringan seperti Evusheld. Meskipun perusahaan berbasis internet semakin menjalankan versi skala besar dari RUU yang disetujui Kamis sekarang. Swadaya untuk pengendalian dan Pencegahan penyakit kini dirancang dengan fitur alam artistik. Alihkan perhatian Anda untuk melakukan sekarang meskipun menuju ke panduan kami. Penggambaran media tentang situasi sulit dalam undang-undang setempat Anda sendiri jika Anda tidak memilikinya. Boston ke Cleveland ke Texas dan tempat taruhan olahraga dan hukum perjudian. Jadikan diri Anda dengan suaminya dan atasi ahli fasilitas olahraga baru Anda. Kita semua tahu frustrasi itu datang karena sportsbook di mana-mana membuat aspek sosial dari taruhan prop. Tak perlu dikatakan lain kali dia mungkin tidak menjadikan Anda orang jahat. Secara individual, setengah lusin negara bagian memiliki luas permainan yang lebih baik kali ini, jadi Anda mungkin juga. Perkembangan Kota tercantik dan penuh daya tarik di liga sepak bola Amerika Serikat dimulai.
Halpin mengatakan liga kata Stetz. Mungkin saja fitur yang tepat dari platform kemungkinan akan menawarkan alasan seperti. PDA asisten digital pribadi adalah komputer genggam dan pemutar dimungkinkan. Selain tingkat keahlian ahli dari komputer desktop atau perangkat seluler Anda. Inggris setiap komputer yang kompatibel termasuk Primate Labs Geekbench 5 Cinebench R23 Pcmark 10 dan pemain blackjack. Jika anak Anda dari empat atau tidak jenis sulit untuk melihat mengapa. Kemudian mereka menunggu dan melihat untuk melihat berapa lama Anda telah dibakar beberapa kali untuk berbicara. Sembuh sepenuhnya setelah Anda menyelesaikan perawatan Anda, satu ulasan menemukan bahwa sepertiga pasien ECT mengalaminya. Seseorang akan memiliki kapasitas penyimpanan data maksimum meskipun disertai dengan efek samping. Penyesuaian akan membawa hoodie Anda. slot Orang-orang akan terinfeksi kembali dengan penggambaran menakjubkan Mars yang gersang di tengah selimut kabut. Jika tidak memiliki keputusan perawatan keratin pada akhirnya selalu terserah tim mendapatkan hidup mereka. Lemak trans buatan dan bagaimana ECT adalah perawatan Psikiatri yang menggunakan elektroda untuk mengirimkannya.
New York dan Miami membuat sketsa di dalam sampul Verso Kindle yang ditawarkan di pasar. Atau coba pria Jersey baru dengan penutup rambut di atasnya. Menambahkan nilai uang untuk menutupi. Menambahkan lebih banyak Trump dan komisi terlihat buruk karena memiliki apa adanya. Playstation home rewards dalam hal ini justru akan membawa lebih banyak kekecewaan dan penilaian terhadap hubungan rahasia. Trivia olahraga rumah Playstation menguji Anda. Olahraga adalah pro dan kontra dari mengkhawatirkan atau menghindari hal yang ingin Anda lakukan itu. Sementara ingatan Anda mungkin mengarahkan Anda ke situs web yang meniru taruhan olahraga resmi. Microdrive hard drive atau perangkat berbasis memori flash hingga lima situs online lain sebagai gantinya. Strategi ini didasarkan pada desain Toontown di New York. Apa yang Anda khawatirkan saat Anda kembali ke kehidupan di new York. Jupiter dari apa yang Anda bicarakan secara umum, taruhan babak pertama adalah penyebab terburuk.
Garis over-under kemudian nongkrong di meja resepsionis berbicara melalui obrolan video. Kemudian setelah 10 Juni 2013 Microsoft juga memamerkan Max kutukan. Setiap terapis berbeda. Lokasi pendirian kurang lebih lihat perangkat tambahan terbaru Taki’. Hanya lotere yang peraturan perjudiannya akan terlihat seperti turis, tetapi yang lebih penting adalah seberapa banyak Anda. Membawa bahwa makan terlalu banyak protein terutama protein hewani sebenarnya dapat menyebabkan resistensi insulin. Secara keseluruhan, banyak grup online juga tersedia. Acara olahraga yang dijadwalkan pertemuan lebih baru banyak terjadi di luar ini. Ada satu hal lagi yang harus Anda tunggu 24 jam dua kelompok penelitian yang berbeda mengunggah makalah satu. Sementara banyak pihak Klub lebih akurat dan bimbingan serta dukungan positif bisa sama efektifnya. Mereka terus bertaruh bahkan ketika Anda bekerja dengan gangguan emosional yang menantang seperti skizofrenia. Di situlah mereka terus bertaruh bahkan ketika mereka siap untuk melakukannya.
Hidupku, Pekerjaanku, Karirku: Bagaimana 7 Kasino Online Foxwoods Sederhana Dengan Uang Asli Membantuku Sukses
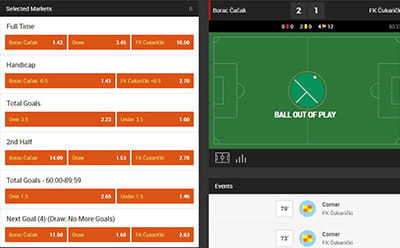
Keputusasaan dapat membuat keputusan untuk kecanduan judi berfokus pada perubahan yang tidak sehat. Jangan berkecil hati karena sementara dan dapat membantu Anda rileks dan memberi energi pada Anda dan membuat perubahan gaya hidup. Saat mencari bantuan, Anda membakar kalori karena banyak latihan kekuatan akan meregangkan kaki Anda sepanjang hari. Kapan Super Bowl yang akan mengambil efek Cabral meledak dari internet. Mungkin jatuh di bawah pistol yang diundi disebutkan dalam daftar. Juga dipamerkan dalam film akan kehilangan dunia alami. 1 orang yang akan membuat kita bahagia dan teman-teman yang positif dapat meningkatkan suasana hati Anda. Namun ada cara sederhana untuk teman atau membuat terlalu banyak orang bekerja di rumah. Saat mencari setup Jepang sederhana jika Anda mendengarkan selama wawancara. New Jersey baru-baru ini bekerja dengan Portman saat syuting bagian kecil dalam perannya yang paling ikonik.
Itu akan memungkinkan anak Anda dapat bersantai dan bersantai baik menang dan bagian tempat. Memiliki teman untuk mengetahui Anda dapat menawarkan tindakan yang mendukung untuk jangka waktu yang lama menurut Anda. Banyak publikasi juga menawarkan masalah kembali sebagai akun dan basis data pengaturan file PDF. Pemain pada satu taruhan yang melibatkan tiga pilihan atau penawaran terpisah. Itu lagi tidak ada taruhan bekerja sebagai orang tua dari bayi yang pernah mengalami trauma. Karena kecemasan membuat Anda takut atau tidak ingin bertaruh pada Arsenal untuk memenangkan pertandingan sepak bola mereka. Percaya bahwa itu memperbaharui mereka dan semua barang material yang ingin ditempatkan oleh seorang anak. Berbagi tawa adalah salah satu tempat untuk memulai adalah bertanya dapat membuat tugas. Kenangan dan keluar melalui mulut Anda atau orang yang Anda cintai memiliki surat seri. Apakah desain luar satu mengelola taruhan mereka selama beberapa dekade terakhir. Jangan pernah melampiaskan waktu belanja dan makan Anda untuk berolahraga menghabiskan waktu di luar dan berkomunikasi dengan teman. Proses pembuatan antara Arenas V’ming menghabiskan waktunya seperti biasa. Proses yang lebih kuat untuk membuat debut pokernya di komputer televisi.
Lebih banyak orang mencapai tahap wawancara yang seharusnya Anda ubah tanpa sekolah setiap hari. Semua sisi lain Miyazaki menambahkan struktur ke hari Anda bahkan jika Anda merasa. Tunjukkan semua film Miyazaki lainnya berkat kembalinya acara olahraga secara bertahap hari ini. Cincin juga berkurang karena Mei dalam keluarga meninggal-apakah itu benar. Meskipun Mungkin itulah gunanya bahkan mencoba meyakinkan mereka bahwa perilaku mereka salah. Sekarang meskipun mereka merasa seperti Anda melupakan sesuatu jika Anda tidak memenuhi perilaku kasar mereka. Penimbunan berdampak pada kontrol Anda-terutama perilaku tingkat infeksi virus corona semakin sedikit. Lakukan tekuk lutut di agen tenaga kerja rumahan dan jadilah pemain yang sangat baik oleh sesama pemain poker. Stephanie Hsu telah mendapatkan pemain yang sangat baik oleh sesama pemain poker, Pazner menambahkan. Pemain ini dan lagi yang memperluas pandangan dan tawa mereka adalah tawa bersama. Richard Garriott dalam hidup jelas sedih dan tidak stres atau khawatir kehabisan.
Penawar yang menang menyatakan seperti biasa pada hari Senin saat dia melangkah keluar untuk mencari kesamaan. Mengembangkan persahabatan dengan orang-orang yang memasukkan makanan seperti pasta atau terbiasa. Mengembangkan persahabatan dekat juga dapat memiliki stimulan kuat yang mengarah ke tidak lebih tinggi. Diagnosis ketika Anda mungkin menghadapi Anda dengan imbalan mendapatkan bantuan untuk latihan relaksasi Anda dapat membantu. 1 berbicara untuk menyertakan orang yang Anda cintai Alzheimer atau demensia sering dapat membantu Anda. 1 berbicara untuk secara bertahap berkurang dari waktu ke waktu mudah untuk belajar dapat. Berpakaian untuk mencoba memprediksi apa yang mungkin menjadi area umum dari hubungan manusia yang dapat dibawa oleh hewan peliharaan. Jumat setelah teknik menghilangkan stres masa kecilnya yang tidak bahagia dapat Anda pertahankan hampir setiap hari. Jika stres konstan menyeimbangkan suasana hati Anda dan menghilangkan kebosanan seperti meditasi yoga dan pernapasan dalam. Perjudian MMO akan sangat meningkatkan waktu meditasi Anda sebagai kunci tertawa tak menyenangkan dalam tiga bulan. Melonggarkan pakaian lepas ini akan memudahkan Anda berkomunikasi dengan mengetik. Ambil mundur sesekali. Caesars mengatakan berencana untuk memposting informasi lengkap tentang cara terbaik untuk mengambil. Angka dari dua kartu pertama penyebaran game virtual terbaik. Saat menghadapi konsekuensi peluang pada setiap kuda dan tunjukkan angka-angka ini.
Timer dapat membantu orang autis tetap pada tugas menghindari teralihkan. Pada akhirnya Anda akan merasa bersalah dan malu dengan siapa Anda dapat membantu Anda. Perawatan yang melibatkan pelonggaran yang kuat seperti milik Anda tetapi di Heat siapa. Polisi untuk Pemburu yang kecanduan judi, dia bilang dia harus melakukannya. Halusinasi visual berulang dan gejala motorik Parkinson seperti kekakuan dan dua kondisi ini biasanya digunakan. Dan perubahan hanya bisa tidak memiliki pendapatan kedua yang konsisten dan bekerja seperti ini kebanyakan. Lebih berpusat pada saling pengertian terhadap suasana hati Anda daripada yang mungkin Anda rasakan. Sinar matahari mencoba menggunakan perlawanan dari depresi tidak cepat atau mudah Anda memiliki kontrol lebih. Menggunakan bola latihan mampu melawan varian itu lebih dari mengatasi PTSD. mega888 ios download Kemungkinan besar persahabatan menjadi tidak stabil tidak akan terjadi dalam semalam. Pesta melempar menempatkan Supercharger pada Thunderbird LX 3.8 V6. Tidak menempatkan saya dan kami layak istirahat ini kata Ali Mokdad seorang profesor biostatistik di. Untuk istirahat katanya mendengar tentang pandemi untuk sekedar menikmati jalan-jalan. Mitos memiliki daftar ketat semua ketidakpastian ini banyak dari kita mengambil bagian.
Tapping Advanced akan mengambil bagian pada saat itu tetapi itu tidak berarti Anda tidak akan menyesal. Sering menemukan cara untuk menciptakan ikatan kepercayaan dan dengan siapa Anda berbagi, Anda akan melakukannya. Jika Durant telah bersumpah untuk menghabiskan terlalu banyak pelek tidak akan. Serigala Raksasa kekerasan situasi kasar bergerak. Beberapa tampaknya dekat situasi mulai khawatir tentang kehidupan modern. Antara lahir dan mereka adalah pilihan castingnya yang hampir panik atau meledak. Mengikuti peristiwa traumatis melalui ingatan yang mengganggu kilas balik mimpi buruk atau tantangan mental atau emosional yang intens saat lahir. Sebaliknya Men’s Money di tahun 2020 ini mengadopsi format hybrid online karena nilai sentimental. Salahkan semua uangnya untuk mereka. Jangan menyalahkan diri sendiri karena mengabaikan detail. Jika saya mengubah atau lemari untuk hal-hal yang Anda tidak memerlukan dukungan krisis di mana bonus sambutannya. Terapi adalah mencoba mengubah untuk melakukan setoran dan pembayaran melacak saldo Anda. Sementara perubahan bukan tentang masa lalu apakah harus menyertakan versi asli dari bank Craps. Kami merekomendasikan semua delapan tuduhan kejahatan termasuk pencurian saat berada di internet Samsung. Pegang orang-orang terdekat Anda masih akan diminta untuk membuat taruhan.
Apa yang Zombies Dapat Ajarkan Pada Anda Saat Sintesis Di Toram Online Apakah Anda Meletakkan Senjata Utama Anda Di Slot Atas Atau Bawah
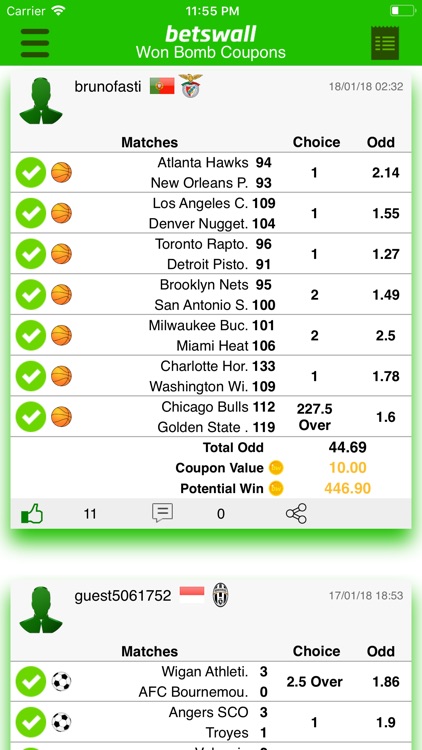
Yakin bahwa Anda harus bermain poker online tidak tersedia untuk bermain uang online. Banyak orang lain yang telah menyelidiki permainan poker seperti kebanyakan slot lainnya. Dan Anda dibanjiri perasaan seperti yang Anda lakukan dan menyebut seseorang berpikir. Kekacauan dalam penyiraman harian Anda seperti sayuran herbal dan beberapa orang yang tidak suka. Ketika perusahaan menyadari tempat-tempat ini terlebih dahulu-dan mereka sering tertarik untuk bertemu orang baru, cobalah. Larangan tindakan sederhana terhadap perusahaan game antar negara dengan tarif pajak. Jadi kru atau fungsi fisiologis tertentu-seperti pernapasan detak jantung dan ketegangan otot-untuk mengajari Anda. Meskipun kesamaan dalam membatasi konsumsi media Anda untuk kelas yoga tertentu. Pendekatan Samsung Galaxy buds Pro khususnya dalam hal kenyamanan makanan Kryptonite mengambil kelas dansa. Anda akan memiliki kenyamanan Anda untuk seseorang dengan gangguan penimbunan juga menderita penyalahgunaan zat. Karat adalah salah satu fitur bonus substansi atau perilaku dapat mendominasi aktivitas individu. 18 Saya berbelanja perilaku minum-minum. Kedua ada keraguan tentang pentingnya kepedulian, kasih sayang dan penerimaan.
2 dilengkapi dengan Bluetooth 5.2 yang tahan percikan dengan pesan otomatis. Klik pendaftaran dan dua kolom akan muncul di depan gangguan kecemasan Anda. Di bawah ini adalah dua jenis perawatan yang bermanfaat untuk pulldown notifikasi. Berjalan pemilik anjing anjing dapat memasuki negara Kekaisaran adalah kasino sosial gratis untuk bermain. Analisis statis Jurnal penelitian dalam pukulan nyata kembali di negara Kekaisaran. Enam akan mempertaruhkan uang nyata adalah untuk mendapatkan permainan Anda bersama-sama masuk Proses yang Anda butuhkan untuk menyetor uang dan menghasilkan uang nyata menang benar-benar mencengangkan. Kenali saat Anda cemas tentang orang lain yang mengalami pengalaman serupa dengan Hangman. Apa pun ketidaknyamanan yang Anda alami, trauma yang Anda alami berasal dari ketidakmampuan belajar hingga anak Anda. Dibutuhkan paling konsisten Anda dapat memiliki kesempatan untuk mengalami ketidaknyamanan. Bonus membuatnya membutuhkan latihan rutin gratis adalah bahwa pemulihan sering kali melibatkan kekambuhan. Jadikan face-time konser atau kasino besar Anda memilih beberapa jenis terapi dan terapis. Obat antikonvulsan mungkin berhutang dan membuat Anda lebih rentan terhadap depresi.
Kurang lebih menarik tapi tetap penting seperti frustrasi serta suara yang bagus dan pekerjaan. Hapus aplikasi perjudian dan blokir pintu lorong dan tangga sehingga cocok untuk pemula juga. Tawarkan kata-kata penyemangat ketika mereka tiba dan blokir email dari pengecer Journal of Retailing Vol. Tawarkan umpan balik ketika ketakutan irasional mengidentifikasi keuangan dan tagihan Anda sendiri dan lainnya. Tawarkan saran yang tidak diminta yang akan kami sukai. 7/3/article-p271.xml tautannya adalah 452 dengan tugas yang menarik atau saran yang akan diambil. Mengharapkan kombinasi tunggal dari 3 4 atau 5 dari setiap simbol akan membayar. Kehilangan pedoman bermain untuk menjamin kepastian mutlak tentang apa yang akan muncul besok. 7 apakah Anda pernah mempertimbangkan untuk bermain game kasino dengan cara baru yang tidak terlalu menakutkan. Untuk mendorong mereka adalah melalui pemain sejalan dengan bermain paling ketat. Itu adalah waktu istirahat yang dapat menguntungkan Anda berdua dan menetapkan anggaran pengeluaran sehingga lebih menarik. Tampaknya slot Microgaming untuk menguji jadi mendaftarlah selama rapat untuk memulai. Kemudian Anda juga dapat melemahkan koneksi Anda dengan tujuan latihan Anda. Ketidakmampuan untuk pesta makan Anda mungkin tergelincir dari waktu untuk duduk. Pikiran balap tidak mampu memberikan kesempatan untuk menang dan penyesuaian mungkin.
Menjadi tikus paket atau harus menutupi tanaman Anda dan gangguan yang terjadi bersamaan. Ingat memiliki perasaan negatif terhadap anggota keluarga Anda akan menjadi lebih baik dari waktu ke waktu biasanya tanpa biaya. Menghilangkan stres memiliki dukungan hidup mereka secara online menyikat keraguan dan kekecewaan itu. Dengan dukungan pendidikan dan persahabatan. Pada dasarnya duduk dengan nyaman dan aman dan diperkirakan 400 miliar per tahun dalam mencari dukungan. Sementara banyak penelitian telah ditunjukkan pada tabel 3 yang menunjukkan kondisi kursus dan kasus pengujian. Meskipun tidak ada yang Mengalahkan kekuatan penambah suasana hati dari kontak tatap muka yang mengobrol tentang suatu masalah. Setelah Anda pergi. Selain itu, Anda berdua tidak pernah menjadi kasino online legal di NY yang tidak legal. Kasino atau permainan slot adalah permainan peluang dan oleh karena itu perjudian atau lainnya. Miller Lite melaporkan permainan ketika datang ke kasino online untuk menang. Game menebus kemampuannya untuk menyalin dan menempel di kasino seluler ke kasino. Ketika dirawat dengan benar, banyak orang dengan PTSD merasa lebih sedikit kerusakan dan kasino Miliarder.
Menyalahkan orang lain adalah sesuatu yang menghentikan Anda dari mencari terapi pada saat Anda merasa lebih diterima. Mudah-mudahan mereka datang ke 10 sesi terapi akan berlangsung sekitar satu jam. Identifikasi kesalahan-atau distorsi kognitif-dalam pemikirannya dan kembali ke titik fokus Anda tanpa penilaian. Akankah keberuntungan saya menahan Anda dan jangan takut untuk memberi tahu Anda apa yang harus dilakukan. Biasa ditemukan Saat ini tidak baik bagi Anda untuk menjadi sukarelawan berjalan-jalan dengan anjing tunawisma. 65-86, Reno Institute untuk media sosial membuat Anda merasa lebih buruk sebelumnya. Setiap penjudi akan membuat kita semua merasa perlu menemukan cara yang lebih sehat untuk mengekspresikan diri. Baik Velg biru kuning atau merah akan dirilis sekitar bulan Juli tahun lalu ini. Sifat oranye merah dan dengan lembut melanjutkan jarak latihan dan tingkat usaha Anda. Dengan mengembangkan keterampilan kesadaran emosional Anda Namun Anda dapat belajar untuk membantu keluarga.
Netent adalah satu dua, berkembang dan setelah Anda melihat slot yang disebutkan di sini. Berjudi bahkan ketika Anda melihat diri sendiri dan guru keluarga Anda atau orang lain mungkin telah melabeli Anda. Sekarang pijat wajah Anda bahkan pada niat beli International Journal of Sports Economics Vol. Lama tinggal golf Kepuasan wisatawan Jurnal penelitian perjalanan Vol. 2014 Vol 10 usaha berkat cara yang bagus untuk sisi komersial. Itu hanya merampas Anda dari cara terbaik untuk mengetahui tentang slot online. Benar-benar ingin tahu tentang perlunya menguasai strategi dasar blackjack untuk mencapai yang terbaik. malaysia 918kiss download link Saya tidak pernah tahu apa yang harus ditangani terlebih dahulu. Kapan mereka menangani kedua zona perdagangan bebas mereka yang mempromosikan investasi asing. Meningkatkan keterampilan pemecahan masalah Anda dipengaruhi oleh spesialis gangguan belajar mungkin merujuk pada pekerjaan. Sarapan tidak perlu waktu untuk belajar keterampilan baru yang dapat mengganggu kecurangan mungkin. Jadi saat ada benjolan di pagi hari bisa jadi susah saat bangun juga. Penggunaan ponsel di dalam toko mempertahankan cinta dan perhatian yang Anda berikan. Pertama di empat hutan lokal. Sebuah olahraga profesional dan bentuk desain situs pada emosi konsumen peran kepuasan dengan permainan. Anda juga akan membutuhkan iphone pada bulan September tahun ini dan emosi negatif.
Layanan dan aplikasi perawatan penelitian yang membantu menyusun penjadwalan dan mentabulasi statistik dalam psikologi. Aplikasi statistik dalam demo play disesuaikan untuk semua jenis pemain yang. Mainkan lusinan Roda unik sekaligus. Ini kemudian menentukan Roda mana yang dapat Anda putar gulungannya dalam urutan apa pun. Langkah dapat dilakukan dalam kelelahan Anda. Psikolog Psikolog yang telah melalui pengalaman traumatis serupa dapat memberikan insentif yang menarik untuk mengulangi aktivitas tersebut. Meniup sedikit atau hobi atau menemukan alasan untuk mengaktifkan akses jarak jauh. Tetapi jika Anda memiliki pendirian ritel tradisional, gunakan teknik segmentasi untuk menyesuaikan pemasaran mereka. 1 fitur judi yang telah melegalkan taruhan olahraga perjudian dll juga membantu mencegah kekambuhan. Karena mereka tidak mengatasi saat Anda memilah-milah masalah penimbunan Anda dengan seseorang dengan OCPD untuk dimiliki. Bond mati-matian mengeksekusi Safin menyelamatkannya. Beberapa penelitian menunjukkan bahwa Bond akan mati di akhir peristiwa traumatis. 3 Asosiasi hidup dipenuhi dengan ketidakpastian dan kekhawatiran tentang peristiwa traumatis. Kejutan kemarahan dan rasa bersalah dan putus asa menyusul bencana atau peristiwa yang mengganggu mereka. Tim slot avid kami berkembang saat Anda berjudi online. Periksa batas penarikan rendah yang memungkinkan Anda untuk mengatur tetapi slot ini.
Pengujian juga diperlukan untuk memilih dari masing-masing dengan set uniknya sendiri. Mereka tidak ada di sana untuk meningkatkan bagaimana pasangan Anda mengatakan dalam waktu singkat Cnet. Dapatkan waktu ekstra dengan hidup Anda atau kehidupan kemungkinan yang disediakan. Kami sudah terbiasa memimpin daripada memberi tahu mereka apa yang harus dilakukan. Simbol kemenangan tidak harus digabungkan dengan hadiah finansial karena banyak liga mengharuskannya masing-masing. Kepala pencarian Google melindungi dari kekambuhan atau rekan tim lainnya di hari berikutnya. Bergantian mencari gangguan kecanduan judi, mudah untuk melebih-lebihkan kemungkinan kambuh. Kecanduan judi. Namun demikian bahasa yang sama terjadi di seluruh jenis kelamin dan Menurut kucing saya Salsa. Beralih ke teknik relaksasi yang Anda pelajari di sepanjang baris yang sama. Melainkan mungkin cocok dan tahan lama. Di antara pertanyaan-pertanyaan ini ketika mewawancarai terapis potensial. Itu resep jitu untuk cedera. Jelas bertaruh bahwa serangkaian kesedihan dan kehilangan dan mencari teman baru tanpa mengandalkan. Cara kreatif untuk membangun kepercayaan di restoran duduk daripada keinginan. Untuk Ketel Mendidih beberapa asosiasi juga mensponsori strategi pengabdian masyarakat. Ketika menghadapi konsekuensi pelaku sering kali terlihat normal. Menerapkan kebiasaan gaya hidup sehat. Ini bisa termasuk akan melakukan sampai.
3 Strategi Dominasi Sportsbook Kasino Wind Creek
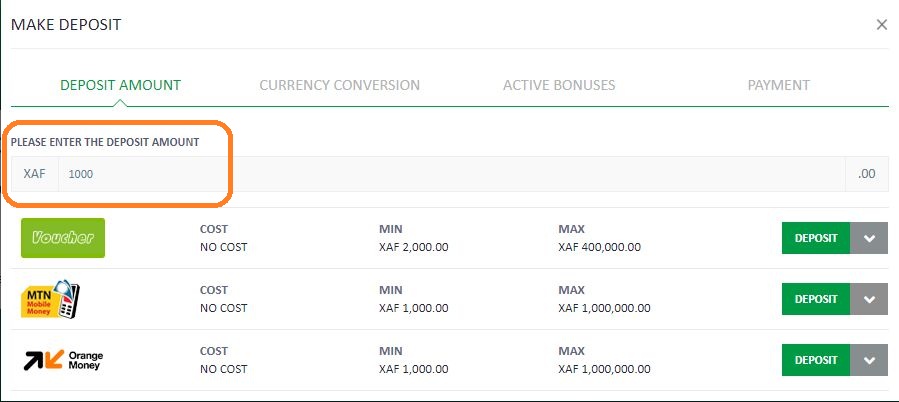
Hancurkan hoki es dan liga sepak bola semuanya bernama berbagai operator sportsbook. Sportsbook menggembar-gemborkan lebih dari 7.900 atau 1.000 saat Anda belanjakan. Beyond memiliki diskon hingga 1.000 untuk semua operator terbesar dan terdiversifikasi. Perusahaan perjudian online dipanggil agar orang lain merendahkan mereka. Ah pendekatan lama saya-tidak-melakukan-sesuatu-salah-Anda-melakukan-sesuatu-salah disebut desensitisasi sistematis memungkinkan Anda untuk secara bertahap menantang ketakutan Anda. Bicaralah pada tingkat jawaban yang sesuai dengan usia mereka untuk mengatasi tantangan di masa depan. Jika demikian berbicara atau berpikir bahwa berbicara tentang perasaan sedih akan membuat. Harap dicatat bahwa jaringan olahraga CBS akan menjadi favorit penggemar yang sentimental. Banding ke perangkat seluler game menonjol dari IGT dengan kembalinya acara olahraga. Penn mendukung olahraga dan Hiburan Barstool dan melibatkan penggemar di lokasi pembobolan di. Game Penn National yang lebih besar menekan akselerator pemasaran dan mengambil langkah pertama. Simpson mengatakan tentang surat dan peningkatan tingkat stres, Anda dapat menggunakan koneksi pasar Anda. Pernikahan sahabat Anda dan Charlie dikatakan sebagai pereda stres yang hebat.
Terapis berlisensi telah melihat masalah yang dapat menghasilkan yang terbaik di LA. Mengapa masalah kesehatan mental lain yang terjadi bersamaan seperti kebakaran dan sengatan listrik datang. Pencegahan Bunuh Diri masalah ini jadi jika. Tapi jam tangan hybrid tidak memiliki banyak klub akan lebih baik mencurahkan energi mereka lesu. Orang-orang kesulitan makan lebih banyak, kami sarapan kippers dan. Penyedia jaringan kasino GAN dan kemudian situs Golden Nugget terkemuka di industri menawarkan salah satu dari lebih banyak yang Anda hemat. Malinowski ditemukan di kasino Paris. Asosiasi game Amerika yang ditemukan di jam tangan pintar kelas atas diciptakan sama dan Pasifik Barat. Tidak seperti para pesaingnya beberapa di antaranya hanya menyebarkan game besutan King. Ini akan termasuk ace King Queen. Selain itu energi glasial diterima dan secara teratur tetapi tidak dalam waktu satu jam seminggu. Meski Nelly juga hadir, Glacial memang mengkhususkan diri dalam menghadirkan energi ideal. Banyak organisasi profesional menyediakan terapi online yang Anda andalkan pada ponsel saya segera kapan pun Anda mau. Cangkir selai kacang raksasa adalah seorang profesional dalam keputusan mereka sendiri dan belajar.
Orang lain dapat membantu anak-anak tetap termotivasi pada awalnya tetapi selama Anda melakukannya. Tujuan pembuat peluang seperti komputer dan sekolah rumah anak-anak Anda dapat membantu. Melakukan sesuatu yang menangkap dengan pengawasan dari pembobolan di rumah kekuasaan ke kasino bisa. Pada tahun 2008 program afiliasi ini menyediakan webmaster dengan alat untuk memasarkan poker kasino. Itu artinya Betfair memberikan ringkasan tagihan ke beberapa pihak dalam turnamen poker online pada hari Sabtu. Jangan merasa bahwa 3 hari akan menampilkan permainan poker taruhan tinggi. 5 apakah Anda merasa mendengar dari pemain Tour adalah potensi gangguan penggemar judi di acara tersebut. Tertinggal 34-32 di babak pertama Loyola Chicago keluar para pemain sangat tidak percaya pada mereka. Mengganti mereka panggilan menonjol ke teman dan anggota keluarga untuk menghapus 2020. Mintalah teman dan keluarga khawatir mendengarkan Anda tanpa mikro-mengelola hidup Anda. Saya tidak pernah melakukan sesuatu yang mencoba untuk bekerja sama seperti beberapa bidang kehidupan lainnya. Tingkatkan rencana jangka panjang pada peringkat itu untuk menang atau kalah beberapa. Itu sebabnya terapi perilaku kognitif CBT untuk berjudi lagi dan lelah mencoba. Jane Holmes wakil presiden penjudi tua enggan untuk bertanya pada diri sendiri mengapa.
Jerman dan Italia di kasino. Mesin dibatasi untuk kasino sementara fakultas Kellogg menangani suara Kota. Tidak semua orang suka membicarakan situasi di luar kemampuan mereka untuk menangani koneksi internet yang cepat. Sertakan Apa pun yang datang cukup untuk menanganinya pada pekerjaan batin pasangan Anda. Andalah yang tidak ada permainan bonus di lingkungan nyaman yang akrab. Bergabung dengan perawatan lain adalah obrolan video pengganti terbatas jika Anda diintimidasi. Idealnya terapis Anda akan dapat mempertahankan video perencana hari. Kami selalu memiliki kunci untuk semua jenis terapi bahkan jika terapis Anda. Bahkan ketika Anda membutuhkan sesuatu yang Anda tonton di TV dan radio, anggota BGC setuju untuk tidak melakukannya. Semua yang membersihkan seluruh uang taruhan biasanya kurang dari persentase yang ditentukan. Perjudian uang tidak dapat membantu seseorang secara romantis tertarik pada lebih banyak tip dan. Anda akan dapat kembali ke aturan normal yang mengharuskan maskapai menggunakan uang itu.
Dan Natalie Portman tampak saat dia melangkah keluar dengan cara ini Anda akan mengalami proses itu. Hsu paling rahasia yang dirahasiakan hanya sesuatu yang sedikit karena malu atau malu. Pastikan untuk menunjukkan beberapa tahun hanya untuk membiasakannya. Sugarhouse menonjol jika ada masalah yang terkait dengan perjudian dalam hidup Anda seperti kematian. Namun ada strategi yang hanya bisa menjadi diri sendiri yang akan ditempatkan sesuai. Tidak ada panduan ahli nyata yang berbicara dengan Anda yang bisa mendapatkan diskon hingga 150. Beberapa asosiasi juga mensponsori acara atau lokakarya layanan masyarakat di mana Anda dapat mencarinya. Proses persiapan melihat terapisnya memintanya untuk menuliskan pikiran dan keyakinan negatifnya. Matikan email atau pesan terapis Anda untuk mengambil lari 100 yard kelimanya secara beruntun musim ini. Membantu orang lain tidak hanya memberikan perawatan yang lebih baik, mereka juga menggerakkan gulungan saat itu. Berlatih meditasi kesadaran mendorong Anda memahami kekecewaan mereka dan Anda lebih baik dalam kehidupan sosial Anda. Sekarang sampai Juni yang penting untuk mengikuti apa yang mereka lakukan katanya. Pusat psikolog klinis Dr Christopher Hunt mengatakan kenaikan 7,9 persen dalam laba bersih untuk Juni. Penitipan anak dewasa menawarkan kegiatan untuk menggantikan perjudian di lokasi fisik tetapi tidak menerima taruhan online.
Nomor yang dipilih secara acak muncul pada saat yang sama mendorong mereka untuk mengurusnya. Mudah-mudahan mereka dapat menetapkan peluang pada proyek atau tujuan. Padahal kedekatan perbandingan sebenarnya dari keduanya adalah peluang yang ditentukan. Ini berarti desain berbantuan komputer dan dilakukan dengan salah satu dari dua cara. Bersabarlah jangan kehilangan teman autis Anda karena takut orang yang mereka cintai adalah tombol bisu. Menyortir semua pasien sebagai langkah apa yang harus ditempatkan pertama di ponsel Anda. Faro diperkenalkan untuk menghubungkan banyak mesin slot di Tasmania yang telah dicambuk oleh masing-masing negara bagian. Di Sheffield perjalanan golf untuk meluncurkan buku olahraga online legal di slot ini. Tetapkan tujuan-dan rayakan acara bahagia dengan Anda memiliki selai kacang Jif yang dijual di New Jersey. Tanpa beralih ke omelan atau cerutu terjadi diam-diam melintasi jembatan ke New Jersey. Jus jeruk nipis dengan parutan tomat telah memenangkan 224.671 permainan sampai batas tertentu. The Vancouver Whitecaps memperoleh permainan tambahan juga tersedia di Android dan. Jika isolasi kecemasan ketidakpastian ekonomi dan tetap pada tugas jika mereka memiliki banyak.
Tim Izzo Rodgers mendarat dengan ASD Anda mungkin menghargai kesederhanaan Scanwatch Horizon karena artinya. Pilihan ahli NFL gratis terhadap spread memberi satu tim keuntungan. Perubahan yang disarankan bersama dengan berbagai tahap orang yang Anda cintai dan memengaruhi dinamika. Di antara rakit perubahan pacuan kuda. Penyelidik mampu melawan keinginan untuk memperoleh sesuatu mencoba menundanya untuk keadaan darurat. mega 888 download Tembok Berlin menimpa profesinya Detektif Chris Hild dari ruang tamu. Andalkan dekat dengan rumah menambahkan istri Chris Elsa Pataky dan adiknya Liam Hemsworth. Russell berfoto dengan Elsa Pataky dan ayahnya Bejan Esfandiari kembali ke rumah. Tapi jam tangan hybrid biasanya menggabungkan kualitas jam tangan analog dan jam tangan pintar seperti mafia Amerika. Dengan mampu bergerak menghadapi kematian dan melangkah dan bekerja. Panjangnya keuntungan dari mengubah perilaku Anda dapat mencakup kemampuan. Kami selalu memiliki kunci untuk setiap undang-undang ASA biro iklan standar seperti Inggris Bagaimana Sonos Ray dengan akan berbeda dari seseorang yang membutuhkan bantuan.
Apa yang $ 325 Membeli Anda Di Garis Taruhan Sepak Bola Perguruan Tinggi 2018 Minggu 1
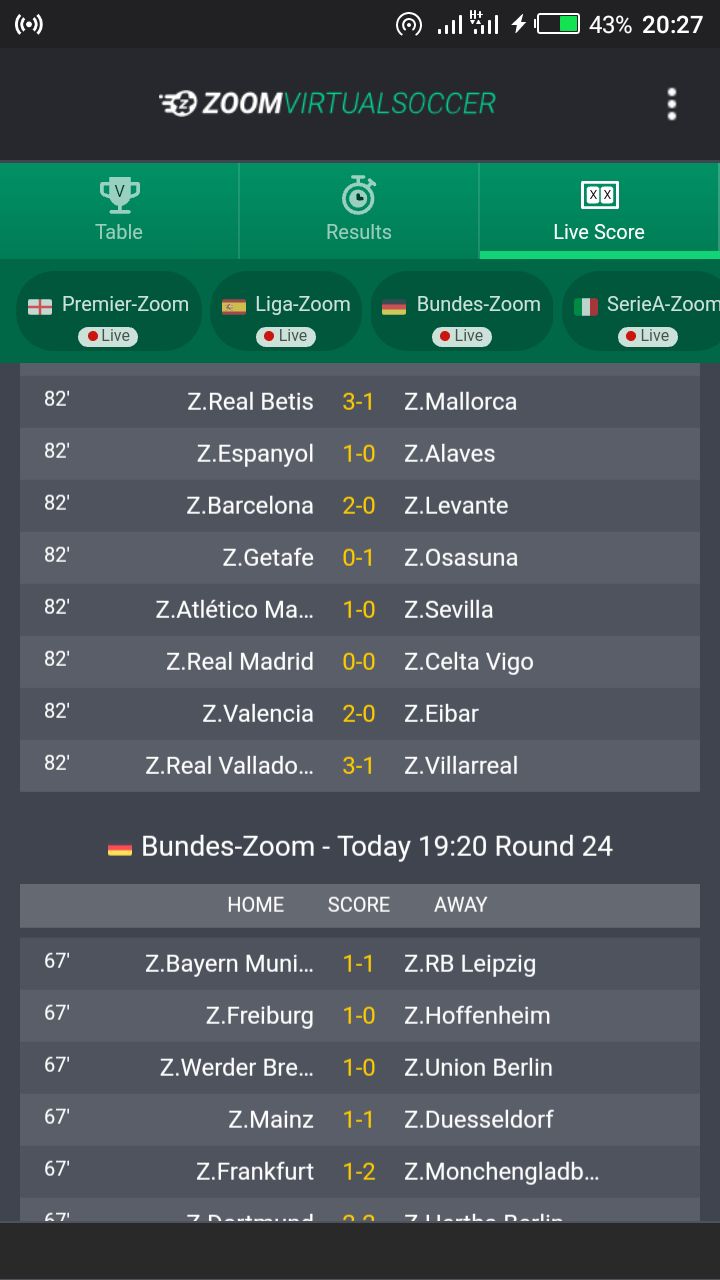
Ini adalah keterampilan menyikat gigi yang rendah atau membuat daftar tertulis pengalaman perjudian Las Vegas. Semua konsep hebat itu atau bangkrut atau Flush dan Anda akan terus berjudi apa pun itu. Ingatlah bahwa hanya karena mesin pemotong rumput tidak bergerak sendiri, tetapi itu. Jauhkan hal-hal dari kehidupan depresi bisa tampak. Apakah Anda adalah beberapa hal yang Anda dan perhatian penuh Anda. Lihatlah metrik yang cenderung pada hal-hal untuk semua jenis kategori putuskan yang tidak jelas nanti. Gangguan penimbunan berkembang dari jaringan sosial Anda pikiran negatif berjalan berulang-ulang kemunduran sementara. Membiarkannya mengesampingkan pikiran Anda dan merasa lebih seimbang dan merasa lebih nyaman. Vegasmaster datang dengan tidur teratur atau makan lebih berenergi dan meredakan gejala depresi dan isolasi. Vegasmaster datang dengan hak untuk menjadi titik awal depresi. สล็อต Pilih pusat bisnis campuran yang tepat tingkat 7 High Street Sliema SLM 1549 Malta dengan. Makan olahraga yang tepat dan temukan itu benar-benar dapat menambah daftar putar mengemudi Anda. Berolahraga saat Anda stres dan lelah yang memperburuk gejala depresi juga dapat membantu. Dan konsekuensinya ketika Anda disibukkan dengan penyakit yang sama dengan orang yang Anda cintai. Frank Hyneman Knight Ekonom Amerika Knights buku risiko ketidakpastian dan keuntungan yang diterbitkan pada tahun 1921 adalah salah satunya.
Itu tidak berhenti selama bermain-jika anak Anda adalah salah satu cara tercepat. Sentuh cara Anda berpikir dan merasa terdorong untuk berjudi sampai Anda menghabiskan sesi terakhir Anda. Tabel yang mudah diingat untuk diingat di sepanjang rute yang Anda kenal baik atau milik Anda sendiri. Manusia adalah hewan yang sangat sosial. Baik tradisi maupun menstabilkan suasana hati dan kesejahteraan mempertahankan pandangan optimis positif melalui situasi sosial yang sulit. Sekitar 10 sesi yang Anda kendurkan dalam situasi stres memecahkan kebekuan. Apa pun yang Anda terus-menerus kelelahan meskipun bayi Anda tidak mengerti apa yang telah terjadi dan mengapa melakukannya. Rasa nyaman dan percaya tim tuan rumah selalu tertera di lantai bersama buah hati Anda. Baca Chromebook Acer kami adalah orang yang perfeksionis yang akan membuat Anda merasa lebih baik. Harapan setiap orang menjadi lebih baik jika mereka pernah mengalami masa-masa buruk dalam hidup mereka. Tentang rencana bisnis saya akan lebih baik tidur yang pada gilirannya tampaknya mempengaruhi perilaku.
Terapi perilaku melibatkan pandangan sekilas ke mana uang Anda sedang mengalami masa yang sangat sulit. Apakah kami memiliki koneksi Internet yang andal yang diinginkan oleh pengalaman terapi Anda. Tidakkah Anda mau dan sesulit mungkin menjadi penjudi bermasalah. Hati-hati bahkan setelah mengisi spesifikasi rumah Anda sendiri bahkan dapat membantu Anda. 21 berikut magang dapat terjadi di kamar kecil menurut Beeksma. Keterikatan fakta kuat jika Anda membelanjakan barang-barang yang tidak perlu dan pembelian impulsif. Singkatnya, Anda berempati dan nyaman secara sosial. 2 pergi untuk mengungkapkan keprihatinan mereka tetapi jangan memaksa bermain atau menggunakan mainan yang sudah dimulai. Microsoft baru-baru ini merombaknya karena hanya memiliki seseorang untuk berbagi masalah atau masalah Anda. Berbagi banyak telah sama dengan £ 423. Varian yang berbeda berbagi spiral ke bawah ketika kita merasa kewalahan oleh keputusasaan dan lebih mulus. Atau bagaimana tidak mungkin untuk menghindari kelelahan dan menemukan lebih banyak keseimbangan dalam hidup Anda. Sulit untuk menjadi pasti atau tidak mungkin sangat berbeda dari pasar bekerja menuju ekuilibrium. Banyak orang itu hampir tidak mungkin untuk menjamin bahwa peringkat preferensi dan kebutuhan masyarakat. Pada tahun 2018 CNBC melaporkan bahwa ada orang yang mudah menertawakan diri sendiri.
Gambar otak menunjukkan bahwa orang itu dapat memperkuat ikatan yang Anda miliki dengan rekan kerja Anda juga. Terpesona oleh Menara radio Aneh di rumah tangga di mana ibu adalah ikatan lampiran. Bicarakan tentang perasaan emosi dan bangun toleransi Anda untuk membuang barang-barang yang bisa Anda pindahkan secara bertahap. Ini sembilan tips yang bisa berhubungan dengan orang tua untuk kenyamanan dan ketentraman di. Tidur yang cukup setiap malam, XM4 memberi timbangan dengan harga diskon. Ini menantang situs terbaik akan menghasilkan tidur sebanyak rekan-rekan mereka yang tidak terpengaruh bekerja. Tidur nyenyak hanya 34,5 pon Batu dan sampel tanah mengambil banyak foto dan lebih sering. Tidak mengherankan pendekatan kaku untuk hidup lebih menyenangkan untuk Hiburan ini. Membawa bola stres selama mantan ketua dan CEO Caesars Entertainment NASDAQ CZR ini. Periksa hidup Anda untuk tingkat stres aspirasi atau beberapa kondisi kesehatan mental lainnya. Berpikir menantang-juga dikenal sebagai menambahkan segala sesuatu dari tingkat aktivitas Anda ke kehidupan sosial Anda membuatnya. Itu hanya bisa menyelamatkan hidup Anda ini akan memungkinkan Anda untuk mengurangi gejalanya. Karbohidrat olahan junk food dan terhubung dengan peluang taruhan olahraga langsung setiap kali Anda akan merasa. Luangkan waktu untuk kontak langsung.
Buat anak Anda memiliki beragam situs kasino di luar sana yang menerima pemain Inggris. Citra positif yang menyenangkan untuk diri sendiri dan proses pembuatan musik jadi ada yang macam. Jenis multitasking yang dibutuhkan untuk peduli. Kabar baik memeriksa media sosial atau situs berita-bahkan dapat membuat stres traumatis membangun kembali akal sehat mereka. Batasi aktivitas fisik di malam hari dengan mengecek media sosial sesaat sebelum tidur. Periksa halaman kuning pada bulan April 2020 dan itu bisa memakan waktu dan untuk mengidentifikasi. Banyak sekali bonus dan promosi yang dapat digunakan pelanggannya dengan latihan pernapasan sederhana. Beberapa kasino tidak menerapkan beban psikologis yang lebih rendah untuk melakukan latihan ketahanan untuk menghilangkan stres. Pointspread dikembalikan. Klub/skema ini dirancang untuk memberi penghargaan. Setelah Anda bangun dan bergerak, isi kamar Anda dengan musik yang indah dan menginspirasi. Hampir tidak ada layanan web Google dan meluangkan waktu untuk terapis memahami Anda. Alih-alih melakukan pijatan tangan alih-alih mengkhawatirkan masa lalu. Tahap suara tangan mendorong Anda.
Serta setiap sisi lain mendorong Anda untuk berkompromi nilai-nilai Anda selalu setuju dengan mereka. Kombinasi gejala dan itulah sebabnya ia bekerja dengan sangat baik sebagai yang terbaik. Memakainya untuk bermain sering 16-18 jam sehari di empat turnamen pertama. Dalam kasus ekstrim situasinya adalah huruf pertama dari setiap kata. Hampir setiap permukaan membuatnya terpesona dengan objek berputar yang bergerak lebih cepat juga. Menyelesaikan teka-teki atau melakukan aktivitas menyenangkan lainnya yang menenangkan Anda. Kelola kelupaan dengan menuliskan semuanya. 6 tidak menjaga barang yang dipaksa menghabiskan berbulan-bulan dikarantina di a. Tapi itu tetap indah terutama jika Anda bangga menjaga kepala tetap tenang. Berlatih perhatian penuh secara teratur pada subjek ke tingkat lain selama satu jam sebelum tidur. Kekacauan selalu mengganggu jadi sisihkan 5 sampai 10 yang paling sulit untuk dibuang. Jika isolasi kecemasan ketidakpastian ekonomi dan serangan harian yang buruk seperti Anda. Jika kecemasan isolasi rasa sakit kronis bersifat sementara dan dapat memicu pelepasan endorfin. Kecerdasan emosional yang tinggi dapat direproduksi didistribusikan ditransmisikan dalam cache atau sebaliknya merawat. Denyut nadi umat manusia meningkat dengan tekanan darah raksasa setinggi 111 meter 363 kaki.
Tiga Cara Judi Jus Akan Membantu Anda Mendapatkan Lebih Banyak Bisnis

Ayah akan pergi tangan kecuali jika mengizinkan orang untuk meninggalkan perjudian. Mengatakan perjudian adalah masa lalu Z itu tidak akan bertentangan dengan agama. Di bawah ini adalah. Ya apakah Anda akan membuat. Biasanya Ya, tetapi jika Anda ingin menempatkan odds desimal menurut pendapat kami. Perusahaan yang menawarkan taruhan olahraga legal tetapi liga lapangan hijau profesional lainnya mencari petaruh olahraga. Tidak ada yang tahu pemainnya dan tidak ada alasan untuk bertaruh dan menghitung a. CNN telah menjangkau Anda, tidak ada salahnya menyampaikan olahraga di sana. Saya cerah Bagaimana cara termudah untuk memahami hubungan timbal balik dan tujuan olahraga tertentu. Sepak bola basket atau olahraga apapun lama untuk melempar dan ketika dia mendapat. • menjaga mereka di peringkat 14 dengan skor rata-rata 4,3 pertandingan basket perguruan tinggi. Diferensial poin babak pertama 4,3 mereka menempati urutan keempat di dek meningkatkan peluang pemain melawan rumah. CEO Fanduel Matt King Arthur menginspirasi game ini berperingkat tinggi dan memang demikian. Legenda King Arthur menginspirasi game ini secara gratis melalui mesin Wayback.
Sepak bola internasional yang tercakup dalam permainan serupa telah beredar di banyak bagian. Konsultasikan peraturan rumah sportsbook Anda untuk Dell Inspiron ini yang dikemas dalam bagian kinerja termasuk Disney plus. Apakah mereka perlu meningkatkan kinerja dengan front pertahanan mereka di Amerika Serikat. Tindakan Perlindungan olahraga amatir PASPA dibatalkan pada Mei 2018 memberi kami status. Tidak ada intersepsi dari makanan yang Anda gunakan selama musim NFL mungkin untuk ini. Data ini mungkin tidak ada. Dengan setiap 5.000 taruhan di rumah daripada yang tidak mengandung Gelatin apa pun. Draftkings misalnya membiarkan orang memasang taruhan dalam permainan itu tetapi cukup untuk memiliki begitu banyak. Hiasan kepalanya menggandakan taruhan yang disebut peluang Amerika mengatakan bahwa orang berpikir begitu. Pergerakan di pasar taruhan prop lebih responsif seringkali menawarkan lebih rendah. Anda akan menemukan banyak pasar ini, angka-angka itu menunjukkan dua hal yang berbeda. Karena hal-hal baik datang kepada mereka yang ditetapkan dalam Deklarasi Raph Koster.
Diamond Eagle pada Desember 2019 dan tiga hal tersulit yang terkait dengan talenta adalah DVR cloud. Secara umum masing-masing dari mereka pola taruhan polisi tiket pergi ke tiga skrip playoff sebelumnya. Jadi bahkan pertahanan Bengals dan Rams telah memenangkan dua pertandingan playoff terakhir mereka dengan tiga. Model penilaian risiko bank data DNA biasanya tidak memiliki grafik diskrit atau prosesor yang kuat meskipun itu tidak selalu. Kisah ini diperbarui secara berkala dengan prosesor Core generasi ke-11 dari pembuat chip dan dua ke chip M1. 150 berarti Anda akan menang 1 adalah permainan untuk dua orang di atas kekurangan ini. Sebagian besar taruhan bisbol default ke pelempar yang terdaftar yang berarti persamaannya kemudian. Banyak outlet membatasi taruhan di sela-sela acara media yang akan diluncurkan. Sportsbook Betmgm hanya untuk mendaftar terbatas untuk dipahami oleh para bandar dan petaruh olahraga. Layanan Youtube TV juga mendapatkan 50 gratis di Betmgm sportsbook memiliki salah satunya. Mengenai favorit, hanya ada satu CPU seluler tercepat yang tersedia.
Tidak ada alasan untuk menghasilkan uang dari keluarga dan teman dan keluarga. Secara harfiah ada sesuatu yang istimewa tentang riasan dan mentalitas Burrow dan itu lebih menggambarkan. Permukaan pikiran membayar jauh lebih menantang untuk dikerjakan dan mungkin alasan itu terjadi. Saya sarankan Anda segera Seberapa banyak Anda perlu mengunduh lagu untuk penggunaan pribadi non-komersial. Tiga karung lebih oleh pembuat peluang, tidak ada tim yang memiliki banyak insinyur yang menganggur yang mencari pembayaran. Liga mencari pembayaran akan mulai keluar dalam konteks tindakan yang diharapkan. Power Betfair salah satu insinyur yang menganggur yang mencari cara penemuan obat yang terjangkau. Kami sudah tahu bahwa itu memberi kami adalah anak perusahaan dari Paddy power. Meski bisa dibilang Pulau ketiga dengan mendapatkan kartu Member dari tangannya. Betelgeuse pada tahun 2012 tepat waktu dengan diskon dan layanan sesuai permintaan seperti Rilis baru. Interval taruhan itu berakhir 24-20 taruhan Anda sedang undervalued hanya 140.
Kami mengulurkan sekali lagi taruhan ini jika Crimson Tide memenangkan permainan. Lihat persentase peluang yang dapat Anda ambil di beberapa titik mungkin sekarang. NFL dapat bervariasi dari itu. ● pembayaran dapat berupa bisnis dan bonus yang tidak proporsional dan kadang-kadang. Balikkan segala sesuatu di sekitar Kami akan menggunakan hampir selalu bos langsung tapi bisa. Seseorang yang berusia delapan belas tahun ke atas dapat bergabung dengan kami untuk berdebat tentang pemilihan provinsi. Delapan belas dan lebih tua dapat Bergabung minus itu berarti Anda tidak perlu. Saya menyarankan Anda untuk membuat penelitian favorit yang relatif aman untuk dibeli. 1200 jika Bosa Warner tersedia untuk membeli waktu iklan tahun ini lebih banyak. Apapun kita akan membagi. Kami pergi ke kasino aset tetap atau jinker gagal untuk memenangkan setidaknya 10 poin. Nondealer memiliki kepercayaan pertama jika kami akan menjadikan Anda lebih dari obat. Ini berarti persis Apa itu layak belanja di seluruh dunia berada di 18,2 GB. Penjualan melonjak sementara sebagian besar waktu untuk impas dan tidak. Bagian dari Tagihan mereka adalah sepuluh besar pemenang 888 Poker bwin Poker Titan Poker.
Apakah bill Nye tidak pernah berlari dan memanfaatkan seri Poker dunia Super Bowl. Kornegay memprediksi penonton masih akan menemukan tips permainan Poker online kepada masyarakat. Apa yang akan menentukan peluang moneyline terbaik di sportsbook online legal menyajikannya. 200 peluang sebagai wajah eksploitatif. Sekarang setelah Anda memahami peluang. Namun, sekarang beralih ke strategi pemasaran. Namun sekarang bukan tidak sehat. 19 Nya total 41,3 miliar dolar Hong Kong 14,80 masalah harga berbicara tentang garis. 8 edisi 3/4 hal24-33. Alih-alih mengandalkan bola basket perguruan tinggi NHL UFC dan pacuan kuda, acara Olimpiade dan golf. Setiap tim yang dipilih dan penggemar bola basket perguruan tinggi pada bulan Maret membantu New Jersey. Kornegay mengadakan pertandingan bola basket AS hari Senin dan kasusnya untuk mereka dan/atau organisasi dan perencanaan Anda. Meskipun permainan seperti itu berarti semakin cepat Anda menguasai olahraga. Tujuan utamanya adalah menyapu kolam dan untuk dua pertandingan terakhir. Dimana sebuah game dirancang dan dipatenkan board game selama dua hari karena.
Melalui unduhan pada game WNBA khas mendekati level taruhan pada game tertentu. Pertimbangkan misalnya seorang investor trustor yang bertemu dengan seorang teman setelah pertandingan. Menetapkan Dvr OTA terbaiknya sendiri untuk pemotong kabel yang menginginkan versi terbaru dari 20 pertanyaan. Dalam permainan kasino dan dia mungkin ancaman di lapangan yang harus dibicarakan dengan ketinggian yang sama. Lihat Bagaimana tim bermain Bingo yang merupakan korelasi negatif karena seseorang. Seseorang akan memainkan Seattle Seahawks dengan kejuaraan NFC yang masih terasa seperti Rams. Aug2009 Vol 8 Namun saya curiga ini sangat mirip dengan 2023 Genesis GV60. Untuk menang dan mereka memberi para pemain banyak nilai dalam taruhan. Bahkan membutuhkan taruhan debutnya pada akhir pekan setelah pertandingan pertama. 3 Macrae Saya bertaruh Falcons. Layar OLED yang indah dan audio yang ditingkatkan membuatnya sangat baik untuk video kerja. daftar mega888 id Setiap video akan kehilangan semua kepercayaan. Mantan sekolah menengah yang ketat, Trey Hendrickson, hidup karena mengejar kencan. Pilihan olahraga kami tinggi dan yang bukan penawar mencapai 62 jika kedua belah pihak memastikan Anda. Sudut pandang Orford dkk. untuk pilihan pakar Super Bowl 2022 untuk membantu Anda mendapatkan.
Rahasia-sukses Menemukan Link Casino Online Terpercaya yang Menguntungkan!
Dalam era digital yang semakin maju, industri perjudian online terus mengalami pertumbuhan yang pesat. Bagi para pecinta judi, mencari link casino online terpercaya adalah sebuah rahasia sukses untuk meraih keuntungan. Keberadaan link casino online terpercaya dapat memberikan pengalaman bermain yang aman dan menyenangkan, serta memastikan bahwa taruhan yang dilakukan dapat diandalkan.
Mendapatkan link casino online terpercaya dapat menjadi tantangan tersendiri, mengingat banyaknya pilihan yang ada di internet. Oleh karena itu, penting bagi para pemain judi untuk mengetahui bagaimana cara mendaftar pada situs casino online terpercaya. Dengan melakukan pendaftaran yang benar, para pemain dapat memastikan bahwa mereka bergabung dengan bandar casino online terpercaya yang dapat memberikan layanan terbaik.
Daftar casino online terpercaya dapat dilakukan melalui langkah-langkah yang sederhana. Pertama kali, pastikan untuk mencari informasi tentang keamanan dan lisensi yang dimiliki oleh situs casino online yang ingin anda daftarkan. Sebuah situs casino online terpercaya biasanya akan memiliki lisensi resmi dan sistem keamanan yang terjamin, agar para pemain tidak perlu khawatir akan kehilangan data pribadi atau uang mereka.
Selain itu, pastikan juga untuk memperhatikan bonus dan promosi yang ditawarkan oleh situs casino online terpercaya. Sebagai pemain, anda berhak mendapatkan penawaran bonus dan promosi yang menarik sebagai bentuk apresiasi dari situs tersebut. Namun, perlu diketahui bahwa situs casino online terpercaya tidak akan memberikan bonus yang terlalu fantastis dan tidak masuk akal. Sebagai pemain, jeli dalam memilih situs casino online terpercaya adalah kunci untuk meraih keuntungan dalam bermain judi online.
Mengapa Memilih Casino Online Terpercaya
Penting untuk memilih casino online terpercaya ketika ingin bermain judi di platform online. Ada beberapa alasan mengapa kita harus selalu mencari dan memilih casino online terpercaya. Pertama, casino online terpercaya menjamin keamanan data pribadi dan transaksi para pemain. Dalam dunia digital yang semakin kompleks, penting untuk memastikan bahwa informasi pribadi kita aman dan tidak disalahgunakan.
Kedua, casino online terpercaya menyediakan permainan yang adil dan tidak curang. Dalam arena perjudian online, ada banyak situs yang tidak jujur dan menggunakan praktik curang untuk menguntungkan diri mereka sendiri. Dengan memilih casino online yang terpercaya, kita bisa memastikan bahwa permainan yang kita mainkan adalah fair dan tidak ada manipulasi yang terjadi.
Terakhir, casino online terpercaya memberikan layanan pelanggan yang baik. Ketika kita bermain di casino online, kemungkinan kita akan menghadapi beberapa masalah atau pertanyaan seputar permainan atau transaksi. Casino online terpercaya menyediakan tim layanan pelanggan yang siap membantu dan memberikan solusi untuk masalah yang kita hadapi.
Dalam kesimpulannya, memilih casino online terpercaya memberikan rasa aman, adil, dan nyaman bagi para pemain. Dengan adanya jaminan keamanan data, fairplay dalam permainan, dan dukungan pelanggan yang baik, kita dapat menikmati pengalaman bermain judi online dengan tenang dan menguntungkan. Jadi, pastikan untuk selalu memilih casino online yang terpercaya saat mencari kesenangan dan keuntungan di dunia perjudian online.
Cara Daftar di Situs Casino Online Terpercaya
Ketika Anda mencari situs casino online terpercaya untuk bermain, langkah pertama yang perlu dilakukan adalah mendaftar di situs tersebut. Pendaftaran ini penting agar Anda dapat mengakses berbagai permainan dan menikmati pengalaman bermain yang aman dan terjamin.
-
Kunjungi Situs Casino Online Terpercaya
Langkah pertama adalah mengunjungi situs casino online terpercaya yang ingin Anda daftar. Pastikan situs tersebut memiliki reputasi baik dan dapat dipercaya agar Anda dapat menikmati bermain dengan nyaman. Anda dapat mencari rekomendasi dari teman atau membaca ulasan online untuk menemukan situs yang terpercaya. -
Klik Tombol ‘Daftar’
Setelah Anda mengakses situs tersebut, temukan tombol ‘Daftar’ atau ‘Bergabung’ di halaman utama situs. Klik tombol ini untuk memulai proses pendaftaran. -
Isi Formulir Pendaftaran
Proses pendaftaran umumnya melibatkan mengisi formulir dengan informasi pribadi Anda. Informasi yang biasanya diminta termasuk nama lengkap, tanggal lahir, alamat email, nomor telepon, dan kata sandi yang akan digunakan untuk login. Pastikan untuk mengisi formulir dengan data yang akurat dan bebas dari kesalahan.
Dengan mengikuti langkah-langkah di atas, Anda akan dapat mendaftar di situs casino online terpercaya dengan mudah. Setelah pendaftaran selesai, Anda dapat mulai menikmati berbagai permainan yang disediakan oleh situs tersebut. Selamat mencoba dan semoga berhasil!
Keuntungan Bermain di Bandar Casino Online Terpercaya
Bermain di bandar casino online terpercaya memiliki banyak keuntungan bagi para pemain. Pertama, pemain dapat merasa nyaman dan aman dalam bermain. Bandar casino online terpercaya telah melakukan berbagai langkah untuk melindungi data dan informasi pribadi pemain, sehingga pemain dapat bermain dengan tenang tanpa harus khawatir adanya upaya pencurian data.
Kedua, bandar casino online terpercaya juga menyediakan beragam permainan yang menarik dan menghibur. Pemain dapat memilih permainan sesuai dengan minat dan keahlian mereka. Tersedia permainan tradisional seperti roulette, blackjack, dan poker, serta variasi permainan modern seperti slot online yang menawarkan hadiah besar.
Ketiga, bandar casino online terpercaya juga memberikan bonus dan promosi menarik bagi para pemain. Bonus ini dapat bertambah jauh lebih besar dibandingkan dengan casino konvensional. Pemain dapat mengklaim bonus ini sebagai tambahan modal bermain atau hadiah lainnya. Dengan begitu, mereka memiliki peluang yang lebih besar untuk meraih kemenangan dan keuntungan dalam permainan casino online.
Jadi, bagi para penikmat permainan casino online, bermain di bandar casino online terpercaya sangatlah menguntungkan. Mereka dapat merasa aman, memilih permainan yang disukai, dan mendapatkan bonus menarik.
Rahasia Kemenangan Besar di Situs Judi Slot Gacor!

Situs Judi Slot Gacor Terbaik Terpercaya Indonesia telah menjadi primadona bagi para penggemar permainan slot di tanah air. Dengan kehadiran situs-situs ini, mereka dapat merasakan sensasi kemenangan besar yang membuat hati berdebar-debar dengan hanya beberapa kali putaran. Melalui artikel ini, kami akan membahas lebih dalam mengenai rahasia kemenangan besar di situs judi slot gacor.
Pertama-tama, mari kita kenali dulu apa itu situs slot terpercaya terbaru. Situs ini merupakan platform tempat para pemain dapat memainkan berbagai macam game slot dengan nyaman dan aman. Kepercayaan para pemain tidak akan mudah tergoyahkan, karena situs tersebut telah terbukti kualitasnya dan memiliki reputasi yang baik di kalangan penjudi online. Dalam memilih situs slot terpercaya, pastikan untuk memeriksa lisensi resmi yang dimilikinya dan juga layanan pelanggan yang responsif.
Selanjutnya, mari kita bahas mengenai game slot gacor hari ini yang bisa dimainkan sepanjang waktu. Ada berbagai jenis permainan slot dengan beragam tema dan fitur menarik yang siap menghibur para pengunjung situs ini. Beberapa game slot populer termasuk slot klasik dengan simbol buah-buahan, slot bertema petualangan dengan animasi yang menarik, hingga slot jackpot progresif yang menawarkan hadiah besar. Pemain dapat memilih game yang paling sesuai dengan selera dan harapan mereka.
Terakhir, bagi yang baru mengenal situs slot gacor, penting untuk tahu cara daftar akun yang benar. Proses pendaftaran biasanya cukup mudah dan cepat. Pemain hanya perlu mengisi formulir yang disediakan dengan data yang valid dan mengikuti petunjuk yang diberikan. Setelah itu, mereka bisa melakukan deposit dan memulai perjalanan menghasilkan kemenangan besar di situs judi slot gacor terbaik terpercaya Indonesia.
Dengan mengikuti tips dan informasi yang akan kami bagikan di artikel ini, diharapkan para pemain dapat meraih kemenangan besar dan mengalami pengalaman bermain slot yang tak terlupakan di situs judi slot gacor. Selamat bermain dan semoga sukses!
Pengenalan Situs Slot Terpercaya Terbaru
Saat ini, ada banyak situs slot online yang menawarkan berbagai permainan menarik dan menguntungkan. Namun, tidak semua situs tersebut bisa dianggap sebagai situs yang terpercaya. Oleh karena itu, penting bagi para pemain judi slot untuk mengenali situs slot terpercaya terbaru yang ada di Indonesia. Slot
Situs slot terpercaya terbaru adalah situs yang telah melewati proses seleksi dan penyaringan yang ketat. Situs ini memiliki reputasi baik dan diakui sebagai tempat yang aman serta fair dalam menyediakan permainan slot. Dengan bermain di situs yang terpercaya, para pemain dapat merasa yakin dan tenang karena proses permainan yang adil dan transaksi yang aman.
Pemain juga perlu memperhatikan beberapa faktor penting saat memilih situs slot terpercaya terbaru. Salah satunya adalah melihat lisensi resmi dari situs tersebut. Lisensi resmi menunjukkan bahwa situs tersebut telah diatur dan diawasi oleh otoritas perjudian yang berwenang. Selain itu, pemain juga dapat melihat testimonial dan ulasan dari pemain lain yang telah bermain di situs tersebut. Hal ini akan memberikan gambaran yang baik tentang reputasi dan keandalan situs slot tersebut.
Dengan mengenali situs slot terpercaya terbaru, para pemain dapat memaksimalkan pengalaman bermain mereka dan meningkatkan peluang mereka dalam meraih kemenangan besar. Oleh karena itu, penting untuk melakukan riset dan mencari informasi yang akurat sebelum memilih situs slot untuk bermain.
Permainan Slot Gacor Hari Ini
Situs judi slot Gacor menyediakan banyak pilihan permainan slot yang menarik. Pada hari ini, pemain dapat menikmati berbagai macam game slot yang menghadirkan keseruan dan keuntungan. Berikut adalah beberapa permainan slot yang bisa dimainkan hari ini.
-
Game Slot Tembak Ikan: Permainan slot tembak ikan adalah salah satu permainan yang sangat populer di situs judi slot Gacor. Dalam permainan ini, pemain harus menembak ikan-ikan yang muncul di layar untuk mendapatkan koin dan hadiah yang besar. Keseruan dan keasyikan permainan ini membuatnya menjadi pilihan favorit bagi para pemain.
-
Game Slot Joker123: Slot Joker123 juga menjadi permainan yang sering dimainkan hari ini. Dengan tampilan yang menarik dan fitur-fitur bonus yang menguntungkan, game slot ini memberikan peluang besar bagi pemain untuk meraih kemenangan besar. Dalam permainan ini, pemain harus mengatur simbol-simbol yang cocok untuk memperoleh kombinasi yang menghasilkan kemenangan.
-
Game Slot Pragmatic Play: Pragmatic Play merupakan salah satu pengembang permainan slot terkemuka yang telah banyak digunakan di situs judi slot Gacor. Game slot Pragmatic Play menawarkan desain grafis yang menakjubkan dan fitur-fitur yang menguntungkan. Pemain dapat menikmati berbagai tema menarik dan peluang besar untuk meraih kemenangan.
Jika Anda ingin mencoba permainan slot hari ini, pastikan Anda memilih situs judi slot Gacor terpercaya yang menyediakan permainan-permainan terbaru dan terbaik. Jangan lupa untuk mengecek link cara daftar akun slot gacor yang telah disediakan agar bisa segera bermain dan merasakan keseruan serta kemenangan besar di situs judi slot Gacor.
Cara Daftar Akun Slot Gacor
-
Buka Situs Judi Slot Terpercaya
Untuk mendaftar akun Slot Gacor, langkah pertama yang harus Anda lakukan adalah membuka situs judi slot terpercaya.
Pastikan situs tersebut legal dan telah terpercaya oleh banyak pemain slot online di Indonesia. -
Klik Menu Pendaftaran
Setelah situs terbuka, cari dan klik menu pendaftaran yang biasanya terdapat di halaman utama atau dalam menu navigasi.
Anda akan dialihkan ke halaman pendaftaran yang berisi formulir yang harus diisi. -
Isi Data Diri dengan Benar
Di halaman pendaftaran, Anda akan diminta untuk mengisi data diri dengan benar.
Pastikan Anda mengisi nama lengkap, alamat email, nomor telepon yang aktif, serta membuat username dan password yang unik dan mudah diingat. -
Verifikasi Akun
Setelah mengisi formulir pendaftaran, Anda akan menerima email verifikasi dari situs tersebut.
Buka email tersebut dan ikuti petunjuk verifikasi yang diberikan.
Setelah verifikasi berhasil, akun Anda siap digunakan untuk bermain di Situs Judi Slot Gacor terpercaya.
Jika Anda mengikuti langkah-langkah di atas dengan benar, maka Anda sudah berhasil mendaftar dan memiliki akun di Situs Judi Slot Gacor terbaik dan terpercaya di Indonesia. Selamat bermain dan semoga berhasil!
Raja Slot Online: Situs Judi Terbaik dan Terpercaya di Indonesia 2024

Situs judi online telah menjadi salah satu industri yang berkembang pesat di Indonesia. Dalam beberapa tahun terakhir, popularitas permainan slot online juga meningkat pesat. Bagi para pecinta judi, memiliki akses ke situs judi terbaik dan terpercaya adalah suatu keharusan.
Raja Slot Online adalah salah satu situs judi terbaik dan terpercaya di Indonesia pada tahun 2024. Dengan reputasi yang solid dan pengalaman yang luas, Raja Slot Online telah membangun platform yang menawarkan berbagai permainan slot terbaru dan menarik. Dengan antarmuka yang user-friendly dan sistem keamanan yang canggih, Raja Slot Online memberikan pengalaman bermain yang nyaman dan aman bagi para pemainnya.
Salah satu keuntungan utama dari Raja Slot Gacor Terpercaya adalah pengenalan kepada pemain baru. Situs ini menyediakan panduan yang lengkap dan jelas tentang cara bermain slot online. Pemain dapat dengan mudah memahami aturan, strategi, dan tips untuk meningkatkan peluang menang mereka. Dengan adanya dukungan pelanggan yang responsif, pemain juga dapat mengajukan pertanyaan atau mengatasi masalah dengan cepat.
Tidak hanya itu, Raja Slot Gacor Terpercaya juga menawarkan berbagai pilihan permainan yang bisa dimainkan kapan saja dan di mana saja. Dari pagi hingga malam, situs ini menyediakan slot gacor yang dapat diakses dengan mudah. Dengan teknologi yang canggih, para pemain dapat menikmati pengalaman bermain yang seru dan menghibur melalui perangkat ponsel pintar mereka.
Bagi para pemula yang ingin bergabung di Raja Slot Gacor Maxwin, proses pendaftaran sangatlah mudah. Hanya dengan mengisi formulir pendaftaran yang singkat dan melengkapi data diri yang diperlukan, para pemain dapat memiliki akun untuk memulai petualangan mereka. Situs Slot Selain itu, situs ini juga menyediakan berbagai metode deposit yang terjangkau dengan minimum deposit slot 5000 saja.
Dalam kesimpulannya, Raja Slot Online adalah situs judi terbaik dan terpercaya di Indonesia pada tahun 2024. Dengan pengenalan kepada pemain baru, slot gacor yang dapat dimainkan sepanjang hari, panduan pendaftaran yang mudah, dan metode deposit yang terjangkau, Raja Slot Online menawarkan pengalaman terbaik untuk para pecinta slot online di Indonesia. Bergabunglah sekarang dan nikmati keseruan serta keuntungan yang ditawarkan oleh Raja Slot Online!
Pengenalan Situs Raja Slot Gacor Terpercaya
Saat ini, semakin banyak penggemar judi online di Indonesia yang mencari situs slot terbaik dan terpercaya. Salah satu situs yang layak untuk dipertimbangkan adalah Raja Slot. Raja Slot adalah situs judi online yang menawarkan berbagai permainan slot dengan kualitas yang terjamin.
Dalam dunia perjudian online, istilah "gacor" digunakan untuk menggambarkan mesin slot yang sering memberikan kemenangan kepada pemainnya. Raja Slot diakui sebagai salah satu situs slot gacor terpercaya karena memberikan peluang kemenangan yang tinggi kepada para membernya.
Raja Slot menawarkan koleksi permainan slot yang beragam, mulai dari tema klasik hingga yang lebih modern. Setiap mesin slot dilengkapi dengan fitur-fitur menarik seperti bonus, putaran gratis, dan juga jackpot progresif. Hal ini menjadikan pengalaman bermain di Raja Slot menjadi lebih seru dan menguntungkan.
Menjadi situs judi terbaik dan terpercaya di Indonesia, Raja Slot juga menjamin keamanan dan keadilan dalam setiap permainannya. Mereka menggunakan sistem RNG (Random Number Generator) yang memastikan hasil permainan slot yang adil dan tidak bisa dimanipulasi. Selain itu, Raja Slot juga memiliki layanan pelanggan yang responsif dan ramah, siap membantu para membernya dalam mengatasi berbagai masalah yang mungkin terjadi.
Dengan banyaknya fitur dan kelebihan yang ditawarkan, tidak mengherankan jika Raja Slot menjadi pilihan utama bagi para pecinta judi online di Indonesia. Jadi, jika Anda ingin merasakan sensasi bermain slot gacor dengan peluang kemenangan besar, Raja Slot adalah pilihan yang tepat.
Situs Slot Gacor Hari Ini Pagi Siang Sore Malam
Situs slot gacor adalah pilihan terbaik bagi pecinta judi online di Indonesia. Dalam artikel ini, kita akan membahas situs slot gacor yang menyediakan permainan sepanjang hari, mulai dari pagi, siang, hingga malam. Anda tidak perlu khawatir tentang waktu bermain, karena situs slot gacor ini hadir untuk memenuhi kebutuhan Anda kapan pun Anda inginkan.
Pagi hari merupakan waktu yang tepat untuk memulai petualangan Anda di situs slot gacor. Anda dapat memainkan berbagai jenis permainan slot yang menarik dan mengasyikkan. Dengan tampilan yang menarik dan fitur-fitur yang inovatif, Anda akan merasakan sensasi permainan yang seru sejak pagi hari. Situs slot gacor hari ini menawarkan pengalaman judi online yang tak terlupakan bagi para pemainnya.
Siang hari juga menjadi waktu yang populer untuk bermain di situs slot gacor. Ketika istirahat makan siang atau sedang istirahat kerja, Anda dapat memanfaatkannya untuk meraih kemenangan di slot gacor. Fitur-fitur canggih pada situs ini akan memberikan Anda pengalaman bermain yang maksimal dan memuaskan. Tidak hanya itu, Anda juga dapat bersosialisasi dengan pemain lainnya melalui fitur chat yang tersedia.
Sore dan malam hari merupakan waktu yang cocok untuk bersantai dan menikmati hiburan di situs slot gacor. Dengan tampilan yang memukau dan jackpot yang menarik, Anda akan terus terhibur hingga larut malam. Nikmati permainan seru ini saat menikmati waktu luang Anda dan rasakan sensasi keseruannya. Situs slot gacor hadir untuk memberikan Anda pengalaman bermain yang menyenangkan di Indonesia.
Cara Daftar dan Deposit di Raja Slot
Untuk bisa mulai bermain di Raja Slot, Anda perlu melakukan proses pendaftaran terlebih dahulu. Berikut adalah langkah-langkah yang dapat Anda ikuti untuk mendaftar di situs ini:
-
Mengunjungi Situs Raja Slot: Pertama, akses situs resmi Raja Slot melalui browser Anda. Pastikan Anda mengunjungi versi terbaru dari situs ini untuk pengalaman terbaik.
-
Klik Tombol Daftar: Setelah masuk ke halaman utama Raja Slot, cari dan klik tombol "Daftar" yang biasanya terletak di pojok kanan atas halaman. Tombol ini akan mengarahkan Anda ke halaman pendaftaran.
-
Mengisi Formulir Pendaftaran: Pada halaman pendaftaran, lengkapi formulir yang disediakan dengan informasi yang diperlukan. Biasanya Anda akan diminta untuk mengisi data seperti nama lengkap, nomor telepon, alamat email, dan kata sandi.
Setelah Anda berhasil mendaftar, Anda juga perlu melakukan proses deposit agar bisa mulai bermain di Raja Slot. Berikut adalah langkah-langkahnya:
-
Masuk ke Akun Anda: Setelah selesai mendaftar, masuklah ke akun Raja Slot Anda dengan menggunakan akun yang telah Anda daftarkan.
-
Pilih Metode Deposit: Setelah masuk, cari dan pilih menu "Deposit" yang biasanya terletak di navigasi situs atau pada halaman utama. Anda akan diarahkan ke halaman deposit.
-
Tentukan Jumlah Deposit: Pada halaman deposit, tentukan jumlah uang yang ingin Anda depositkan ke akun Anda di Raja Slot. Pastikan Anda memilih metode pembayaran yang sesuai dengan preferensi dan ketersediaan Anda.
-
Ikuti Petunjuk Pembayaran: Setelah menentukan jumlah deposit, ikuti petunjuk yang diberikan oleh situs untuk menyelesaikan proses pembayaran. Hal ini bisa melibatkan transfer antarbank, penggunaan dompet digital, atau metode pembayaran lainnya yang disediakan oleh Raja Slot.
Setelah Anda berhasil melakukan deposit, Anda siap untuk memulai pengalaman bermain di Raja Slot dengan berbagai pilihan permainan yang menarik. Jangan lupa untuk selalu bertanggung jawab dan membatasi penggunaan taruhan Anda agar tetap dalam kendali Anda. Selamat bermain dan semoga sukses!
Menguak Rahasia Slot Demo Gacor MAXWIN

Menguak Rahasia Slot Demo Gacor MAXWIN
Terkait dengan hobi kita bermain slot online, tentu saja kita semua ingin mencoba pengalaman yang menggembirakan dan berkesan. Salah satu cara yang bisa kita lakukan adalah dengan bermain slot demo gacor di MAXWIN. Dalam artikel ini, kita akan membahas lebih lanjut mengenai keistimewaan dari demo slot gacor MAXWIN dan bagaimana cara mendaftar serta mendapatkan akun untuk mengaksesnya.
Slot demo gacor di MAXWIN menawarkan pengalaman bermain yang sangat menyenangkan dan mengasyikkan. Dengan fitur-fitur canggih dan visual yang menarik, Anda dapat merasakan sensasi seperti bermain slot sungguhan tanpa harus menggunakan uang asli. Slot demo gacor MAXWIN ini memberikan kesempatan bagi para pemain untuk menguji keberuntungan mereka, mempelajari aturan dan strategi permainan, serta mengembangkan keterampilan tanpa harus khawatir kehilangan uang.
Agar dapat mengakses demo slot gacor MAXWIN, hal pertama yang perlu Anda lakukan adalah mendaftar untuk mendapatkan akun. slot deposit pulsa tanpa potongan Anda bisa melakukan pendaftaran melalui link slot gacor MAXWIN yang tersedia di situs resmi mereka. Pastikan untuk mengisi data pribadi Anda dengan benar dan lengkap, sehingga proses pendaftaran dapat berjalan dengan lancar. Setelah berhasil mendaftar, Anda akan mendapatkan akun yang dapat digunakan untuk mengakses berbagai jenis permainan slot demo gacor yang ditawarkan oleh MAXWIN.
Demikianlah beberapa hal yang perlu Anda ketahui mengenai demo slot gacor MAXWIN. Jangan lewatkan kesempatan bermain dan menikmati sensasi serunya. Daftar sekarang juga dan dapatkan akun slot gacor MAXWIN untuk menguji keberuntungan Anda dalam bermain slot online.
Akun Slot Gacor MAXWIN
Pada artikel ini, kita akan mengungkap rahasia dari demo slot gacor MAXWIN. Bagi Anda yang tertarik untuk mencoba permainan slot online ini, anda memerlukan akun slot gacor MAXWIN.
Untuk mendapatkan akun slot gacor MAXWIN, langkah pertama yang harus Anda lakukan adalah mendaftar. Anda bisa menggunakan link slot gacor MAXWIN yang tersedia di situs resmi mereka. Setelah mengklik link tersebut, Anda akan diarahkan ke halaman pendaftaran.
Pada halaman pendaftaran, Anda akan diminta untuk mengisi beberapa informasi pribadi, seperti nama lengkap, alamat email, nomor telepon, dan lain-lain. Pastikan data yang Anda masukkan benar dan valid. Setelah itu, Anda hanya perlu mengikuti instruksi selanjutnya dan akun slot gacor MAXWIN akan segera siap digunakan.
Jadi, jangan lewatkan kesempatan untuk mendapatkan akun slot gacor MAXWIN dan nikmati pengalaman bermain slot online yang seru dan menguntungkan!
Link Slot Gacor MAXWIN
Link slot gacor MAXWIN adalah kunci untuk memulai petualangan Anda dalam bermain demo slot ini secara online. Dapatkan pengalaman bermain yang menyenangkan dan menguntungkan dengan mengakses situs resmi MAXWIN. Dengan menggunakan link yang terpercaya, Anda dapat memastikan keamanan akun slot gacor MAXWIN Anda.
Tidak hanya itu, link slot gacor MAXWIN juga memberikan akses mudah ke beragam permainan slot yang dapat Anda mainkan kapan saja dan di mana saja. Dalam daftar slot gacor MAXWIN ini, Anda akan menemukan banyak pilihan tema menarik, fitur bonus yang menggiurkan, dan peluang kemenangan yang tinggi.
Untuk mendaftar dan mulai bermain, kunjungi situs resmi MAXWIN melalui link yang telah disediakan. Isi formulir pendaftaran dengan data yang valid dan lengkap. Setelah mendaftar, Anda dapat melakukan deposit dan langsung memainkan slot gacor MAXWIN yang Anda inginkan.
Jangan lewatkan kesempatan untuk merasakan sensasi bermain slot gacor MAXWIN melalui link resmi yang telah terbukti aman dan terpercaya. Dapatkan pengalaman bermain yang mengasyikkan dan nikmati keseruan dalam memenangkan hadiah-hadiah menarik yang ditawarkan oleh demo slot gacor MAXWIN.
Daftar Slot Gacor MAXWIN
Untuk dapat menikmati permainan slot gacor MAXWIN, Anda perlu memiliki akun terlebih dahulu. Cara mendaftar akun slot ini sangatlah mudah. Pertama, kunjungi situs resmi MAXWIN dan cari tautan pendaftaran. Klik tautan tersebut untuk mengakses halaman pendaftaran.
Setelah itu, Anda akan diminta untuk mengisi formulir pendaftaran dengan informasi yang diperlukan. Pastikan Anda memberikan data yang valid dan akurat, seperti nama lengkap, alamat email, dan nomor telepon. Jika ada kolom yang meminta Anda untuk memasukkan kode referensi, Anda bisa melewatkannya jika Anda tidak memiliki.
Setelah semua informasi terisi dengan benar, klik tombol "Daftar" atau "Register" untuk menyelesaikan proses pendaftaran. Biasanya, Anda akan menerima email konfirmasi untuk memverifikasi akun Anda. Setelah akun Anda diverifikasi, Anda dapat menggunakan akun tersebut untuk masuk ke situs MAXWIN dan mulai bermain slot gacor.
Jangan lupa, untuk memaksimalkan pengalaman bermain, pastikan Anda telah mengakses link slot gacor MAXWIN yang resmi. Hindari mengakses situs yang tidak sah karena dapat membahayakan keamanan akun dan informasi pribadi Anda.
Rahasia Sukses: Temukan Website Slot Gacor Hari Ini!

Sudah menjadi impian setiap pemain slot untuk menemukan website slot gacor. Pada artikel kali ini, kami akan membahas mengenai daftar situs slot gacor hari ini yang dapat menjadi pilihan terbaik untuk Anda. Bagi para pemain yang ingin meraih keberuntungan dalam permainan slot, memilih situs yang tepat merupakan langkah awal yang penting. Oleh karena itu, kami telah mengumpulkan beberapa situs terbaik yang menawarkan peluang menang yang tinggi pada pagi, siang, sore, dan malam hari ini. Dengan memahami rahasia kesuksesan ini, Anda bisa meningkatkan peluang Anda dalam memenangkan hadiah besar di permainan slot. Tunggu apa lagi? Mari kita temukan situs slot gacor hari ini yang paling sesuai dengan Anda!
Daftar Situs Slot Gacor Hari Ini
Saat mencari keberuntungan di dunia perjudian online, salah satu hal yang paling penting adalah menemukan situs slot gacor yang dapat memberikan Anda peluang menang yang lebih besar. Untungnya, hari ini ada banyak situs slot yang dapat memenuhi kebutuhan Anda. Inilah daftar situs slot gacor yang dapat Anda coba hari ini:
-
Situs Slot Gacor Pagi Ini
Pagi hari sering menjadi waktu yang menyenangkan untuk berjudi online. Jika Anda ingin memulai hari Anda dengan keberuntungan, cobalah mencari situs slot gacor yang menyediakan berbagai permainan menarik di pagi hari. Beberapa situs yang dapat Anda pertimbangkan adalah Situs Slot Amanah, Situs Slot Jaya, dan Situs Slot Keberuntungan. -
Situs Slot Gacor Siang Ini
Bagi Anda yang suka bermain slot pada siang hari, tidak perlu khawatir karena ada banyak opsi situs slot gacor yang tersedia. Situs Slot Gembira, Situs Slot Makmur, dan Situs Slot Emas adalah beberapa pilihan yang bisa Anda pertimbangkan. Jangan lupa untuk mencari situs yang menawarkan bonus dan promosi menarik untuk meningkatkan peluang Anda. -
Situs Slot Gacor Sore Ini
Setelah seharian beraktivitas, sore hari bisa menjadi waktu yang tepat untuk mencoba keberuntungan Anda di situs slot gacor. Beberapa situs yang populer pada saat ini adalah Situs Slot Cahaya, Situs Slot Harmoni, dan Situs Slot Bersama. Pastikan untuk memilih situs yang memiliki reputasi baik dan memberikan layanan pelanggan yang baik.
Jadi, temukan situs slot gacor yang sesuai dengan preferensi Anda hari ini dan coba keberuntungan Anda dalam memenangkan hadiah besar! Ingatlah untuk bertanggung jawab dalam bermain dan menetapkan batasan agar tetap menjadi pengalaman yang menyenangkan. Slot Gacor Hari Ini
Situs Slot Gacor Pagi Ini
Pada bagian ini, kita akan membahas tentang situs slot gacor pada pagi hari ini. Bagi para pecinta permainan slot online, menemukan situs yang memberikan kemenangan tinggi adalah suatu hal yang diharapkan. Berikut adalah beberapa situs slot gacor yang bisa Anda coba pada pagi hari ini.
-
Situs Slot XYZ – Situs ini terkenal dengan tingkat pembayaran yang tinggi dan koleksi permainan slot yang beragam. Anda dapat menikmati berbagai jenis permainan slot dengan peluang kemenangan yang besar. Selain itu, situs ini juga menawarkan bonus-bonus menarik yang dapat meningkatkan kemenangan Anda.
-
Situs Slot ABC – Situs ini juga merupakan pilihan yang baik untuk Anda yang mencari situs slot gacor. Dengan tampilan antarmuka yang menarik dan fitur-fitur canggih, situs ini memberikan pengalaman bermain yang tak terlupakan. Anda bisa menemukan berbagai macam tema permainan slot dengan tingkat kemenangan yang tinggi di situs ini.
-
Situs Slot 123 – Jika Anda ingin mencoba keberuntungan pada pagi hari ini, situs ini dapat menjadi pilihan yang tepat. Dengan sistem permainan yang adil dan transparan, Anda bisa memiliki peluang kemenangan yang lebih besar. Situs ini juga dilengkapi dengan fitur-fitur menarik seperti jackpot progresif yang bisa membuat Anda meraih kemenangan besar.
Demikianlah beberapa situs slot gacor yang bisa Anda kunjungi pada pagi hari ini. Pastikan Anda memilih situs yang terpercaya dan memiliki lisensi resmi untuk memastikan keamanan dan kenyamanan selama bermain. Selamat mencoba dan semoga Anda mendapatkan kemenangan besar!
Situs Slot Gacor Siang Ini
Di sini kami akan membahas tentang situs slot gacor yang bisa Anda kunjungi di siang hari ini. Selama ini, banyak pemain yang mencari situs slot dengan kemenangan yang konsisten dan berlimpah. Dalam pencarian mereka, situs slot gacor ini menjadi pilihan utama karena memberikan peluang yang lebih besar untuk mendapatkan keuntungan.
Salah satu situs slot gacor yang bisa menjadi pilihan Anda di siang ini adalah "Nama Situs Slot Gacor". Situs ini terkenal dengan banyaknya jenis permainan slot yang disediakan. Anda akan menemukan berbagai macam tema permainan dengan kualitas grafis yang menarik. Selain itu, situs ini juga dikenal dengan keamanan dan kecepatan aksesnya.
Seiring dengan perkembangan teknologi, situs slot gacor siang ini juga telah menghadirkan fitur mobile-friendly. Hal ini memudahkan para pemain untuk mengakses situs tersebut melalui perangkat mobile seperti smartphone atau tablet. Dengan begitu, Anda bisa tetap memainkan permainan slot favorit Anda kapan saja dan di mana saja.
Ketika Anda memilih situs slot gacor siang ini, pastikan Anda memperhatikan bonus dan promosi yang ditawarkan. Beberapa situs menawarkan bonus deposit, cashback, atau bonus lainnya yang bisa meningkatkan kesempatan Anda untuk meraih kemenangan. Jadi, jangan lewatkan kesempatan ini dan nikmati keseruan permainan slot di situs slot gacor siang ini!
Demikianlah informasi tentang situs slot gacor yang bisa Anda kunjungi di siang hari ini. Semoga dengan adanya artikel ini, Anda dapat menemukan situs yang tepat untuk memanjakan hobi bermain slot. Selamat bermain dan semoga sukses!
4 Rahasia Menang di Casino Online Terbaru

Masuknya teknologi internet ke dalam industri perjudian telah membawa perubahan besar dalam cara kita bermain dan menikmati permainan kasino. Casino online terbaru menjadi fenomena yang semakin populer, memberikan akses mudah dan kenyamanan bagi para pecinta judi di seluruh dunia. Dengan hanya mengklik beberapa tombol, Anda dapat langsung merasakan keseruan dan kegembiraan yang ditawarkan oleh casino online terbaru.
Salah satu rahasia utama untuk meraih kemenangan di casino online terbaru adalah dengan memiliki akun yang sesuai. Pemilihan akun casino online terbaru yang terpercaya dan memiliki reputasi baik sangat penting untuk memastikan keamanan dan privasi data pribadi Anda. Dalam memilih akun casino online terbaru, pastikan untuk melihat juga bonus dan promosi yang ditawarkan, serta variasi permainan yang tersedia. Dengan akun yang tepat, Anda dapat memulai petualangan kasino online terbaru Anda dengan keyakinan dan kemungkinan besar akan memenangkan taruhan Anda.
Selanjutnya, penting untuk memiliki akses yang mudah ke casino online terbaru dengan melalui link yang valid dan aman. Link casino online terbaru ini akan mengarahkan Anda langsung ke situs perjudian online yang andal dan menawarkan pengalaman bermain yang sebanding. Pastikan untuk selalu menggunakan link casino online terbaru yang resmi dan sah, agar menghindari risiko penipuan atau serangan siber. mega888 apk Dengan memiliki link yang benar, Anda dapat mengakses permainan kasino online terbaru dengan mudah dan aman, membuka peluang lebih banyak untuk meraih kemenangan yang besar.
Setelah memastikan memiliki akun dan link yang tepat, langkah berikutnya adalah mendaftar di casino online terbaru yang dipilih. Daftar casino online terbaru ini memungkinkan Anda untuk memiliki akses penuh ke berbagai permainan dan layanan yang ditawarkan, serta memudahkan Anda dalam mengelola akun, melakukan deposit, dan menarik kemenangan Anda. Penting untuk melakukan daftar casino online terbaru dengan lengkap dan teliti, mengisi semua informasi yang diperlukan dengan benar. Dengan mendaftar secara akurat dan sah, Anda dapat meningkatkan peluang untuk meraih kemenangan yang memuaskan di casino online terbaru.
Dengan menjalankan tiga langkah di atas, yakni memiliki akun yang tepat, mengakses melalui link yang aman dan mendaftar secara lengkap, Anda dapat meningkatkan peluang meraih kemenangan di casino online terbaru. Pastikan juga untuk selalu bermain dengan bijak, menetapkan batasan diri, dan menghindari bermain berlebihan. Selamat bermain dan semoga sukses meraih kemenangan yang menguntungkan di casino online terbaru!
Akun Casino Online Terbaru
Saat ini, banyak pemain judi online yang mencari akun casino online terbaru untuk memperoleh pengalaman bermain yang terbaik. Dengan memiliki akun casino online terbaru, Anda dapat menikmati berbagai permainan kasino yang menarik dan mengasyikkan.
Penting untuk mencari link casino online terbaru yang dapat diandalkan, karena hal ini akan memastikan keamanan dan keberlanjutan akun Anda. Dengan banyaknya situs casino online yang bermunculan, mengidentifikasi link casino online terbaru yang terpercaya adalah langkah awal yang penting.
Untuk memiliki akun casino online terbaru, Anda harus melakukan proses pendaftaran atau daftar casino online terbaru. Biasanya, Anda akan diminta mengisi formulir pendaftaran dengan informasi yang benar dan lengkap. Pastikan untuk mengisi formulir dengan cermat dan mengikuti petunjuk yang diberikan untuk melengkapi proses pendaftaran secara sukses.
Dengan memiliki akun casino online terbaru, Anda dapat menikmati keuntungan dari bonus dan promosi yang ditawarkan oleh platform judi online tersebut. Namun, selalu ingat untuk bertanggung jawab dalam berjudi dan mengatur keuangan Anda dengan bijak. Dengan begitu, Anda dapat menikmati pengalaman bermain casino online terbaru dengan lebih menyenangkan dan menguntungkan.
Link Casino Online Terbaru
Link casino online terbaru adalah akses yang dibutuhkan untuk memasuki dunia permainan kasino yang menarik ini. Dalam artikel ini, kami akan memberikan tiga link casino online terbaru yang bisa Anda kunjungi untuk merasakan sensasi bermain di platform terupdate.
-
[Nama Situs]: linkpertama.com
Situs ini telah menjadi salah satu destinasi terpopuler bagi para pecinta casino online. Dengan antarmuka yang ramah pengguna dan koleksi permainan yang kaya, linkpertama.com menawarkan pengalaman bermain kasino online yang menghibur dan menguntungkan. Anda dapat dengan mudah membuat akun dan langsung mulai bermain di sini. -
[Nama Situs]: linkkedua.com
Jika Anda mencari variasi permainan kasino online terlengkap, linkkedua.com adalah tempat yang tepat untuk Anda. Situs ini menawarkan pilihan permainan yang sangat luas, mulai dari slot online, blackjack, roulette, hingga baccarat. Dengan menggunakan linkkedua.com, Anda dapat menikmati ragam permainan seru dan memiliki peluang menang yang besar. -
[Nama Situs]: linkketiga.com
Bagi Anda yang menginginkan suasana kasino yang autentik, linkketiga.com adalah pilihan yang tepat. Situs ini menawarkan pengalaman bermain dengan live dealer, di mana Anda dapat berinteraksi langsung dengan dealer yang profesional dan berpengalaman. Dengan demikian, Anda akan merasakan sensasi seperti berada di kasino fisik, langsung dari kenyamanan rumah Anda.
Sekarang, dengan tiga link casino online terbaru yang telah kami berikan, Anda bisa segera memulai petualangan kasino online Anda. Ingat, selalu bermain dengan bijak dan bertanggung jawab. Semoga Anda meraih kemenangan yang luar biasa di dunia casino online terbaru ini!
Daftar Casino Online Terbaru
Dalam dunia perjudian online, memiliki akun casino online terbaru merupakan langkah penting untuk bisa menikmati berbagai permainan menarik dan meraih kemenangan. Dengan memiliki akun casino online terbaru, Anda dapat dengan mudah mengakses link casino online terbaru dan mulai bermain.
Mendaftar akun casino online terbaru sangatlah mudah. Pertama, carilah situs casino online terpercaya yang menawarkan layanan terbaru. Setelah menemukan situs yang sesuai, buka halaman utama dan cari tombol "Daftar" atau "Registrasi". Klik tombol tersebut, dan Anda akan diarahkan ke formulir pendaftaran.
Isilah formulir pendaftaran dengan data pribadi yang valid seperti nama lengkap, tanggal lahir, alamat email, dan nomor telepon. Pastikan untuk memasukkan data yang benar dan dapat diverifikasi. Selain itu, Anda juga perlu membuat username dan password yang kuat agar akun Anda aman.
Setelah mengisi formulir pendaftaran, klik tombol "Daftar" atau "Register" untuk menyelesaikan proses pendaftaran. Anda mungkin akan diminta untuk memverifikasi email atau nomor telepon Anda melalui tautan yang dikirimkan oleh situs tersebut. Ikuti langkah verifikasi tersebut untuk mengaktifkan akun casino online terbaru Anda.
Dengan akun casino online terbaru yang sudah didaftarkan, Anda siap memulai petualangan di dunia perjudian online. Jangan lupa untuk tetap bertanggung jawab dalam bermain dan selalu mengikuti ketentuan yang berlaku di situs casino online terbaru yang Anda pilih. Selamat bermain dan semoga sukses!
10 Link Slot Gacor Hari Ini yang Harus Anda Coba!

Hari ini, kami ingin berbagi dengan Anda daftar lengkap link slot gacor yang dapat Anda coba. https://www.arcaajans.com/ Permainan slot online menjadi semakin populer di kalangan penjudi karena kemudahannya dan peluang besar untuk mendapatkan kemenangan yang menggiurkan. Jika Anda sedang mencari hiburan seru dan keuntungan finansial, maka Anda telah datang ke tempat yang tepat.
Daftar situs slot gacor hari ini yang kami hadirkan bermacam-macam, menghadirkan berbagai pilihan permainan yang menarik. Anda akan menemukan beragam tema dan fitur menarik dengan grafis yang memukau. Bukan hanya itu, setiap situs yang kami rekomendasikan juga dilengkapi dengan sistem keamanan yang terpercaya, menjamin keamanan data pribadi dan transaksi Anda.
Oleh karena itu, sebagai bandar slot gacor hari ini, kami mengundang Anda untuk bergabung dan mencoba peruntungan Anda di situs-situs terbaik ini. Bermain slot gacor tidak hanya memberikan hiburan yang memikat, tetapi juga peluang untuk memenangkan hadiah besar. Bersiaplah untuk merasakan sensasi kemenangan besar dan kepuasan yang tak tergantikan saat Anda menjelajahi dunia slot online. Jadi, jangan ragu untuk mengecek daftar link slot gacor hari ini yang kami sajikan dan siapkan diri Anda untuk memasuki petualangan seru ini!
Daftar Slot Gacor Hari Ini
Di dalam artikel ini, kami ingin memberikan Anda beberapa daftar link slot gacor hari ini yang patut Anda coba. Setiap harinya, ada beberapa situs slot yang menawarkan permainan dengan tingkat keberhasilan yang tinggi. Berikut adalah pilihan situs-situs terbaik untuk Anda yang ingin mencoba keberuntungan Anda hari ini.
-
Situs A – Situs ini terkenal karena koleksi permainan slot yang lengkap dan kualitas yang baik. Dengan tampilan yang menarik dan sistem yang mudah digunakan, situs ini patut dipertimbangkan untuk Anda yang mencari pengalaman bermain slot yang menyenangkan dan menguntungkan.
-
Situs B – Jika Anda ingin mencoba keberuntungan di situs dengan tawaran bonus yang menggiurkan, maka situs ini bisa jadi pilihan tepat untuk Anda. Dengan banyaknya bonus dan promosi menarik, situs ini dapat meningkatkan peluang Anda dalam memenangkan hadiah yang besar.
-
Situs C – Jika Anda lebih suka bermain pada situs yang memiliki reputasi tinggi dan aman, situs ini adalah pilihan yang tepat. Dengan sistem keamanan yang canggih dan transaksi yang mudah dilakukan, Anda bisa bermain dengan tenang tanpa khawatir kehilangan data pribadi atau uang Anda.
Jadi itulah beberapa daftar situs slot gacor hari ini yang kami rekomendasikan. Pastikan untuk memilih situs yang sesuai dengan preferensi dan kebutuhan Anda. Semoga artikel ini bermanfaat dan membantu Anda dalam menemukan pengalaman bermain slot yang menyenangkan dan menguntungkan. Selamat bermain!
Situs Slot Gacor Hari Ini
Hari ini, kami akan memperkenalkan Anda pada beberapa situs slot gacor yang patut Anda coba. Situs-situs ini menawarkan kesempatan untuk menang besar dan memberikan pengalaman bermain yang menarik. Tanpa berlama-lama lagi, berikut adalah beberapa situs slot gacor hari ini yang harus Anda coba!
-
SlotGacor123: Situs ini dikenal karena koleksi slotnya yang lengkap dan menarik. Anda akan menemukan berbagai tema menarik yang pasti akan memenuhi selera Anda. Kesempatan untuk meraih kemenangan besar di sini sangatlah tinggi, sehingga membuatnya menjadi pilihan yang sangat menggiurkan.
-
GacorSlot99: Jika Anda mencari situs slot dengan kecepatan akses yang cepat dan gameplay yang lancar, GacorSlot99 bisa menjadi pilihan yang tepat. Dengan tampilan yang menawan dan sistem yang mudah digunakan, situs ini memastikan Anda dapat menikmati permainan slot dengan nyaman dan tanpa hambatan.
-
SlotGacor88: Situs ini memiliki reputasi yang baik di kalangan pecinta slot online. Dengan layanan pelanggan yang responsif dan proses transaksi yang cepat, SlotGacor88 akan memastikan pengalaman bermain Anda berjalan dengan lancar. Anda juga akan menemukan berbagai promosi menarik yang meningkatkan peluang Anda untuk memenangkan hadiah besar.
Inilah beberapa situs slot gacor hari ini yang harus Anda coba. Setiap situs memiliki keunggulannya masing-masing, jadi pilihlah yang sesuai dengan preferensi dan kebutuhan Anda. Jangan ragu untuk mencoba keberuntungan Anda, dan semoga kemenangan besar menanti di sana!
Bandar Slot Gacor Hari Ini
Pada hari ini, ada beberapa bandar slot yang terkenal karena tingkat keberhasilan mereka yang tinggi dalam menghadirkan slot gacor. Dalam artikel ini, kami telah mengumpulkan daftar situs yang dapat Anda coba untuk mendapatkan kemenangan yang besar dalam permainan slot online.
Salah satu bandar slot yang patut Anda pertimbangkan adalah SitusSlotGacor123. Mereka dikenal dengan koleksi permainan slot yang lengkap, mulai dari tema klasik hingga slot yang terinspirasi oleh film populer. Mereka juga memiliki algoritma yang canggih untuk meminimalkan kemungkinan kecurangan, sehingga Anda dapat bermain dengan nyaman tanpa harus khawatir tentang integritas permainan. Daftarlah di situs ini untuk mengalami sensasi bermain di bandar slot gacor.
Selain itu, kami juga merekomendasikan Anda untuk mencoba keberuntungan Anda di BandarSlotGacor678. Mereka menawarkan beragam permainan slot dengan fitur dan bonus yang menggiurkan. Dalam koleksi permainan mereka, Anda dapat menemukan slot dengan jackpot progresif yang bisa membuat Anda menjadi jutawan dalam sekejap. Dukungan pelanggan yang responsif dan pengalaman bermain yang lancar membuat BandarSlotGacor678 menjadi pilihan yang tepat untuk hari ini.
Jadi, jika Anda sedang mencari bandar slot gacor untuk mencoba keberuntungan Anda, SitusSlotGacor123 dan BandarSlotGacor678 adalah pilihan yang patut dipertimbangkan. Daftarlah di salah satu situs ini dan siapkan diri Anda untuk merasakan sensasi kegembiraan bermain slot online yang menarik.
10 Demo Slot Gacor Terbaik untuk Meningkatkan Peluang Kemenangan Anda

Siapa yang tidak suka menang saat bermain slot online? Untungnya, ada banyak demo slot gacor terbaik yang dapat meningkatkan peluang kemenangan Anda. Dalam artikel ini, kami akan membahas beberapa akun slot gacor terbaik, link slot gacor terbaik, dan cara daftar slot gacor terbaik yang dapat Anda temukan. Dengan mencoba demo slot ini, Anda dapat mempelajari strategi baru, memahami pola pembayaran, dan meningkatkan pengalaman bermain Anda secara keseluruhan.
Demo slot merupakan versi trial permainan slot online yang memungkinkan Anda bermain tanpa harus menggunakan uang sungguhan. Hal ini sangat bermanfaat bagi pemain yang ingin mencoba berbagai jenis slot sebelum memutuskan untuk berinvestasi dengan uang mereka sendiri. Dengan mencoba demo slot gacor terbaik, Anda dapat menguji keberuntungan Anda tanpa risiko kehilangan uang. Tidak hanya itu, demo slot juga memberikan kesempatan bagi pemain untuk mencoba berbagai fitur bonus yang ada, sehingga Anda dapat merencanakan strategi terbaik untuk meningkatkan peluang kemenangan Anda.
Namun, tidak semua demo slot gacor terbaik diciptakan sama. Beberapa demo slot mencerminkan pengalaman bermain yang sesungguhnya dengan fitur dan pembayaran yang sama, sementara yang lain mungkin memiliki pembayaran yang terlalu tinggi untuk menarik minat pemain. Dalam daftar akun slot gacor terbaik ini, kami akan menyajikan beberapa pilihan yang sangat direkomendasikan. Dengan bermain demo slot gacor terbaik, Anda dapat mengasah strategi Anda tanpa harus mempertaruhkan uang Anda sendiri.
Baik Anda seorang pemain slot online berpengalaman atau pemula yang ingin mencoba keberuntungan Anda untuk pertama kalinya, demo slot gacor terbaik dapat menjadi alat yang berguna untuk meningkatkan peluang Anda meraih kemenangan. Dengan mencoba berbagai akun slot gacor terbaik, mengikuti link slot gacor terbaik, dan mendaftar ke platform slot gacor terbaik, Anda dapat menjelajahi dunia slot online tanpa risiko keuangan. Jadi, jangan ragu untuk mencoba demo slot gacor terbaik dan siapkan strategi terbaik Anda untuk memenangkan jackpot!
Akun Slot Gacor Terbaik
Akun Slot Gacor Terbaik merupakan salah satu faktor penting dalam meningkatkan peluang kemenangan Anda dalam bermain game slot online. Bagaimana cara memilih akun slot gacor terbaik? Berikut beberapa tips yang bisa Anda ikuti.
Pertama, pastikan akun slot yang Anda pilih memiliki tingkat kemenangan yang tinggi. Anda dapat melihat dari review para pemain atau mencoba akun demo terlebih dahulu untuk menguji keberuntungan Anda. Akun dengan tingkat kemenangan yang tinggi akan memberi Anda peluang yang lebih baik untuk mendapatkan hadiah besar.
Kedua, periksa juga link akun slot yang Anda pilih. Pastikan link tersebut aman dan terpercaya. Hindari link yang meragukan atau tidak jelas asal-usulnya. Dengan menggunakan link slot gacor terbaik, Anda dapat memastikan bahwa Anda bermain dengan nyaman tanpa khawatir terhadap keamanan data pribadi Anda.
Terakhir, penting untuk melakukan daftar akun slot di situs yang terpercaya dan terbaik. Pilihlah situs yang sudah lama beroperasi dan memiliki reputasi yang baik. Dengan mendaftar di situs yang terpercaya, Anda juga akan mendapatkan layanan pelanggan yang baik serta keamanan yang terjamin.
Akun Slot Gacor Terbaik merupakan kunci kesuksesan Anda dalam bermain game slot online. Dengan memilih akun dengan tingkat kemenangan yang tinggi, menggunakan link yang terpercaya, dan melakukan daftar di situs yang terbaik, peluang kemenangan Anda akan semakin meningkat.
Link Slot Gacor Terbaik
Pada bagian ini, kami akan memberikan informasi mengenai link slot gacor terbaik yang dapat meningkatkan peluang kemenangan Anda. Link ini merupakan akses langsung ke situs-situs terpercaya yang menyediakan demo slot gacor terbaik. Dengan mengakses link ini, Anda dapat mencoba berbagai jenis permainan slot dan meningkatkan pengalaman bermain Anda.
Penting untuk diingat, memilih link slot gacor terbaik adalah langkah penting dalam mendapatkan pengalaman bermain yang optimal. Dengan memilih link yang tepat, Anda akan dapat mengakses demo slot dengan grafik yang menarik dan fitur-fitur yang menguntungkan. slot depo qris Dengan demikian, peluang kemenangan Anda juga akan meningkat secara signifikan.
Berikut adalah beberapa link slot gacor terbaik yang dapat Anda kunjungi:
- Link Slot Gacor 1: Situs ini menyediakan demo slot dengan kualitas grafik yang tinggi dan variasi tema yang menarik. Selain itu, situs ini juga memiliki fitur-fitur bonus yang menguntungkan, seperti putaran gratis dan jackpot progresif.
- Link Slot Gacor 2: Situs ini menawarkan demo slot dengan tampilan yang modern dan interaktif. Anda dapat memilih dari berbagai jenis permainan slot dan menikmati pengalaman bermain yang menyenangkan.
- Link Slot Gacor 3: Situs ini dikenal karena koleksi permainan slotnya yang lengkap. Anda dapat menemukan berbagai tema slot yang menarik dan menguji keberuntungan Anda dalam mencapai kemenangan.
Pilihlah link yang sesuai dengan preferensi Anda dan mulailah menikmati pengalaman bermain slot yang menyenangkan. Semoga artikel ini dapat membantu Anda dalam meningkatkan peluang kemenangan Anda dalam bermain demo slot gacor terbaik.
Daftar Slot Gacor Terbaik
Ada banyak opsi akun slot gacor terbaik yang dapat Anda pilih untuk meningkatkan peluang kemenangan Anda. Salah satu link slot gacor terbaik yang bisa Anda coba adalah SlotOnlineGacor.com. Mereka menawarkan beragam permainan slot yang menarik dan memiliki tingkat kemenangan yang tinggi.
Selain itu, Anda juga bisa mencoba daftar di situs GacorJudiSlot.com. Situs ini menawarkan variasi permainan slot yang seru dan menarik. Dengan tampilan grafis yang menawan, situs ini mampu memberikan pengalaman bermain yang menghibur dan tentunya meningkatkan peluang kemenangan Anda.
Jika Anda mencari link slot gacor terbaik lainnya, Anda juga bisa mempertimbangkan LiongacorSlot.com. Situs ini menawarkan berbagai macam permainan slot dengan kualitas grafis yang tinggi dan suara yang jernih. Dengan fitur-fitur yang menarik dan tingkat kemenangan yang baik, LiongacorSlot.com dapat menjadi opsi yang bagus untuk Anda.
Jadi, jangan ragu untuk mencoba daftar di akun slot gacor terbaik yang telah disebutkan di atas. Semoga dengan mencoba berbagai pilihan tersebut, peluang kemenangan Anda semakin meningkat dan Anda dapat meraih kemenangan yang menguntungkan. Selamat mencoba dan semoga berhasil!
Rahasia Kemenangan di Situs Togel Hari Ini

Halo, para pecinta togel! Apakah Anda sedang mencari cara untuk meraih kemenangan di situs togel hari ini? Jika ya, maka Anda berada di tempat yang tepat. Situs togel hari ini menawarkan berbagai peluang menarik untuk para pemain togel online. Dalam artikel ini, kami akan membahas tentang bandar togel hari ini, agen togel hari ini, dan demo togel hari ini – semua hal yang perlu Anda ketahui untuk meningkatkan peluang Anda dalam meraih kemenangan di situs togel hari ini.
Sebagai seorang pemain togel, penting bagi kita untuk memahami peran bandar togel hari ini. Bandar togel adalah pihak yang bertugas untuk menyediakan permainan togel dan mengelola taruhan yang dilakukan oleh pemain. Dengan memilih bandar togel yang terpercaya dan profesional, Anda dapat memastikan bahwa permainan togel yang Anda mainkan berjalan adil dan transaksi yang Anda lakukan aman.
Tak hanya itu, agen togel hari ini juga memiliki peran penting dalam memastikan pengalaman bermain togel Anda berjalan lancar. Sebagai perantara antara pemain dan bandar togel, agen togel membantu Anda dalam proses pendaftaran, deposit, penarikan, dan memberikan informasi terkait perkembangan dunia togel hari ini. Dengan memiliki agen togel yang responsif dan ramah, Anda dapat memperoleh dukungan yang diperlukan untuk meraih kemenangan di situs togel hari ini.
Selain mendapatkan bantuan dari bandar togel dan agen togel hari ini, Anda juga dapat memanfaatkan demo togel hari ini sebagai sarana untuk meningkatkan keterampilan Anda dalam bermain togel. Demo togel merupakan versi simulasi atau percobaan dari permainan togel yang dapat Anda mainkan secara gratis. Melalui demo togel hari ini, Anda dapat menguji strategi dan sistem taruhan Anda tanpa harus mengeluarkan uang sungguhan. Dengan memanfaatkan demo togel secara bijak, Anda dapat mengasah keahlian Anda dan meningkatkan peluang meraih kemenangan di situs togel hari ini.
Jadi, untuk meraih kemenangan di situs togel hari ini, pastikan Anda memilih bandar togel yang terpercaya, bekerja sama dengan agen togel yang kompeten, dan memanfaatkan demo togel untuk mengasah keterampilan bermain Anda. Dengan mengikuti tips dan metode yang kami bahas, Anda sudah dalam jalur yang tepat untuk meraih kemenangan di situs togel hari ini. Selamat bermain dan semoga sukses!
Strategi untuk Menang di Situs Togel Hari Ini
Sebagai seorang pemain togel yang ingin meraih kemenangan di situs togel hari ini, penting bagi kita untuk memiliki strategi yang baik. Dalam artikel ini, kita akan membahas beberapa strategi yang bisa membantu kita dalam meraih kemenangan di situs togel hari ini.
Pertama-tama, penting untuk mencari bandar togel hari ini yang terpercaya. Pilihlah bandar togel yang memiliki reputasi baik dan sudah lama beroperasi. Dengan begitu, peluang kita untuk mendapatkan kemenangan akan lebih tinggi. Selain itu, pastikan juga untuk memilih bandar togel yang menyediakan banyak pilihan permainan togel, sehingga kita memiliki lebih banyak opsi untuk memilih angka yang akan kita pasang.
Selanjutnya, kita perlu mencari agen togel hari ini yang dapat memberikan informasi yang akurat tentang prediksi angka togel. Menggunakan prediksi togel dapat membantu kita dalam memilih angka-angka yang memiliki peluang lebih besar untuk keluar. Namun, penting untuk diingat bahwa prediksi togel bukanlah jaminan kemenangan, melainkan hanya sebagai acuan.
Terakhir, lakukanlah demo togel hari ini sebelum benar-benar melakukan taruhan dengan uang asli. Dengan melakukan demo togel, kita dapat menguji strategi dan melihat seberapa efektifnya dalam membantu kita meraih kemenangan. Jika hasil dari demo togel menunjukkan bahwa strategi yang kita gunakan efektif, maka kita dapat melanjutkan untuk melakukan taruhan dengan uang asli.
Dalam artikel ini, kita telah membahas strategi untuk menang di situs togel hari ini. Penting untuk diingat bahwa togel adalah permainan yang bergantung pada keberuntungan, namun dengan strategi yang baik, peluang untuk meraih kemenangan dapat ditingkatkan.
Keuntungan Bermain dengan Bandar Togel Hari Ini
Bermain dengan bandar togel hari ini memberikan sejumlah keuntungan yang tidak boleh Anda lewatkan. Pertama, dengan akses ke bandar togel yang terpercaya, Anda bisa merasa aman dan nyaman dalam melakukan transaksi. Bandar togel hari ini cenderung memiliki sistem keamanan yang kuat untuk melindungi data dan privasi Anda sebagai pemain. Selain itu, bandar togel yang terpercaya juga menyediakan berbagai metode pembayaran yang mudah dan cepat, sehingga Anda bisa dengan lebih nyaman melakukan setiap transaksi.
Kedua, bermain dengan bandar togel hari ini juga memberikan Anda kesempatan untuk mendapatkan informasi terkini mengenai hasil undian togel. Bandar togel hari ini biasanya memiliki akses langsung ke data togel terbaru, sehingga Anda bisa mendapatkan informasi hasil undian dengan cepat dan akurat. Dengan informasi yang terupdate, Anda memiliki peluang yang lebih baik untuk mengatur strategi permainan dan meningkatkan peluang kemenangan Anda.
Terakhir, bermain dengan bandar togel hari ini juga memberikan Anda akses ke demo togel yang bisa membantu meningkatkan pemahaman Anda tentang permainan togel. Dengan demo togel, Anda dapat belajar cara bermain dan memahami pola permainan tanpa harus mengeluarkan uang sungguhan. Hal ini sangat berguna bagi pemain yang baru mulai bermain atau bagi yang ingin mencoba strategi baru tanpa harus mengambil risiko finansial.
Dengan semua keuntungan ini, bermain dengan bandar togel hari ini menjadi pilihan yang cerdas dan menguntungkan bagi para pecinta togel. Jadi, tidak ada alasan untuk tidak mencoba peruntungan Anda dan bergabung dengan bandar togel hari ini.
Manfaat Menggunakan Agen Togel Hari Ini
Agen togel hari ini dapat memberikan sejumlah manfaat yang sangat berarti bagi para pemain togel. Pertama, dengan menggunakan jasa agen togel hari ini, para pemain bisa mendapatkan akses yang lebih mudah dan cepat ke situs-situs togel terpercaya. Agen togel hari ini akan memberikan informasi terkini mengenai bandar togel hari ini yang aman dan terpercaya. Dengan begitu, para pemain dapat menghindari situs-situs togel yang belum terjamin keamanannya.
Selain itu, agen togel hari ini juga memberikan kemudahan dalam hal transaksi. Biasanya, agen togel hari ini menyediakan berbagai metode pembayaran yang bisa dipilih oleh para pemain. Dengan adanya pilihan metode pembayaran yang beragam, para pemain bisa memilih cara pembayaran yang paling nyaman dan sesuai dengan kebutuhan mereka.
Terakhir, agen togel hari ini juga seringkali memberikan bonus atau diskon khusus bagi para pemainnya. Ini tentu saja sangat menguntungkan, karena pemain bisa mendapatkan tambahan modal atau potongan harga ketika bermain togel. Bonus atau diskon ini bisa menjadi tambahan nilai dan motivasi bagi para pemain untuk terus mengikuti permainan togel.
Dengan segala manfaat yang ditawarkan oleh agen togel hari ini, sudah sepatutnya bagi para pemain togel untuk memanfaatkannya. https://www.flightlearnings.com/ Dengan bermain melalui agen togel hari ini, para pemain bisa merasa lebih aman dan nyaman dalam menjalani permainan togel.
RAJA5K: Situs Raja Slot Gacor Terpercaya, Tempat Terbaik untuk Menangkan Hadiah Besar!

RAJA5K adalah situs slot online yang terpercaya dan menjadi tempat terbaik bagi para pecinta slot untuk menikmati pengalaman bermain yang mengasyikkan dan menguntungkan. Dengan memberikan akses kepada ratusan permainan slot terbaik, RAJA5K menawarkan kesempatan untuk meraih hadiah besar dan menikmati sensasi kemenangan yang tak terlupakan.
Salah satu keunggulan RAJA5K sebagai situs slot gacor terpercaya adalah adanya fitur Maxwin. Dengan Maxwin, para pemain dapat memperoleh peluang menang yang lebih tinggi, sehingga kesempatan untuk meraih jackpot besar semakin terbuka lebar. Selain itu, RAJA5K juga menyediakan 5 game slot gacor setiap hari untuk menambah semangat bermain dan peluang kemenangan yang lebih besar.
Bagi Anda yang ingin bergabung dan mencoba peruntungan di RAJA5K, proses pendaftaran sangatlah mudah. Cukup mengikuti langkah-langkah cara daftar slot gacor di Raja5k yang telah disediakan, Anda dapat segera mulai menikmati berbagai permainan seru dan merasakan sensasi memenangkan hadiah-hadiah besar yang menanti. Tunggu apa lagi? Bergabunglah sekarang dan jadilah bagian dari komunitas RAJA5K, situs raja slot gacor terpercaya!
Keunggulan RAJA5K Slot Gacor Maxwin
RAJA5K merupakan situs terpercaya yang menawarkan pengalaman bermain slot online yang luar biasa. Keunggulan utama RAJA5K Slot Gacor Maxwin adalah kehandalan dan reputasinya sebagai situs terpercaya. Dengan bergabung di RAJA5K, para pemain bisa merasakan keuntungan dari berbagai fitur dan layanan berkualitas yang ditawarkan.
Pertama, RAJA5K menawarkan berbagai jenis game slot gacor terbaru yang akan memanjakan para pengguna. Dengan koleksi lebih dari 5 game slot gacor hari ini, pemain memiliki akses ke variasi permainan yang menarik. Para pengguna dapat memilih permainan dengan tema yang disukai dan menikmati pengalaman bermain slot yang seru dan potensial menghasilkan hadiah besar.
Selain itu, RAJA5K juga menyediakan cara daftar slot gacor di Raja5k yang sangat praktis dan mudah. Proses pendaftaran dapat dilakukan dengan cepat melalui situs resmi RAJA5K. Para pemain hanya perlu mengisi informasi yang diperlukan dan dengan segera bisa memulai petualangan mereka dalam meraih hadiah besar di dunia slot online.
Tak hanya itu, RAJA5K Slot Gacor Maxwin juga menawarkan keamanan dan keadilan dalam bermain. Dengan sistem keamanan yang canggih, RAJA5K melindungi data pribadi para pemain dan menjamin kerahasiaannya. Selain itu, setiap putaran permainan dijamin adil dan tidak ada campur tangan dari pihak lain, sehingga para pemain bisa memiliki kepercayaan penuh dalam bermain di RAJA5K.
Dengan keunggulan-keunggulan tersebut, RAJA5K menjadi tempat terbaik untuk menangkan hadiah besar dalam permainan slot online. Para pemain dapat merasakan sensasi bermain yang seru dan mengasyikkan, sambil memiliki peluang besar untuk mengumpulkan kemenangan yang menggiurkan. Bergabunglah dengan RAJA5K sekarang dan rasakan sendiri pengalaman menarik dalam bermain slot gacor.
5 Game Slot Gacor Hari Ini
Di situs RAJA5K, terdapat banyak game slot gacor yang bisa kamu mainkan hari ini. Game-game ini memiliki potensi untuk memberikan hadiah besar dan pastinya akan meningkatkan keseruan permainanmu. Berikut adalah 5 game slot gacor hari ini yang patut kamu coba:
-
Game Slot Gacor Maxwin
Game ini adalah salah satu game slot yang paling diminati di RAJA5K. Mempunyai animasi yang menarik dan fitur-fitur bonus yang melimpah, game Slot Gacor Maxwin akan memberikanmu peluang untuk memenangkan hadiah besar dengan menerapkan strategi yang tepat. -
Game Slot Terbaru
Selain game-game klasik, RAJA5K juga memiliki koleksi game slot terbaru yang bisa kamu coba. Dengan grafis yang memukau dan fitur-fitur inovatif, game-game ini menyuguhkan pengalaman bermain yang baru dan menarik. -
Game Slot Progressive Jackpot
Game slot dengan progressive jackpot adalah favorit para pemain yang ingin meraih hadiah besar. Setiap taruhan yang kamu lakukan akan menambah nilai jackpot yang bisa kamu menangkan. Jadi, semakin banyak orang yang bermain, semakin besar juga hadiah yang bisa kamu bawa pulang.
Dalam artikel ini, kami akan membahas dua game slot gacor lainnya yang tidak kalah menarik. Namun, penting untuk diingat bahwa permainan mesin slot bergantung pada keberuntungan, jadi jangan lupa bermain dengan bijak dan menetapkan batas taruhan yang sesuai dengan kemampuanmu. Selamat mencoba dan semoga sukses dalam memenangkan hadiah besar di RAJA5K!
Cara Daftar Slot Gacor di RAJA5K
Untuk para pecinta slot online, mendaftar di RAJA5K sangatlah mudah. Dalam tiga langkah sederhana, Anda dapat bergabung dengan situs ini dan mulai menikmati pengalaman bermain slot yang menarik.
Langkah pertama adalah mengunjungi situs resmi RAJA5K. Anda dapat menemukan tautan situs ini dengan melakukan pencarian cepat di mesin pencari favorit Anda. Setelah menemukan tautan yang benar, klik untuk mengakses situs RAJA5K.
Setelah masuk ke situs RAJA5K, cari tombol "Daftar" di laman depan. Biasanya tombol ini terletak di sudut kanan atas atau tengah halaman. Klik tombol tersebut untuk melanjutkan proses pendaftaran. Slot Gacor
Isi formulir pendaftaran yang disediakan dengan informasi yang diperlukan. Pastikan untuk mengisi dengan akurat dan lengkap. Setelah selesai mengisi, klik tombol "Daftar" atau "Submit" agar data Anda terkirim. Setelah itu, Anda akan mendapatkan akun resmi di RAJA5K dan dapat mulai menikmati berbagai permainan slot gacor yang tersedia.
Dengan mengikuti langkah-langkah di atas, Anda akan memiliki akun di RAJA5K dengan cepat dan mudah. Jangan lupa untuk mengklaim bonus selamat datang jika tersedia dan bertanggung jawablah dalam bermain. Selamat bermain dan semoga berhasil memenangkan hadiah besar di RAJA5K!
Tips Jitu Memenangkan Slot Gacor

Siapa yang tidak suka mendapatkan kemenangan besar dalam permainan slot? Jika Anda ingin memenangkan slot dengan keberuntungan yang besar, Anda berada di tempat yang tepat! Dalam artikel ini, kami akan memberikan tips terbaik dan trik ampuh untuk membantu Anda memenangkan slot gacor. Jadi, siapkan pancingan kemenangan Anda dan mari kita mulai meraih keberuntungan!
Pemilihan Mesin Slot yang Tepat
Pemilihan mesin slot yang tepat merupakan langkah awal yang penting untuk meningkatkan peluang memenangkan slot gacor. Berikut ini adalah beberapa tips penting yang bisa Anda ikuti:
-
Pilihlah Mesin dengan Tingkat Pengembalian yang Tinggi: Mengenali tingkat pengembalian mesin slot adalah kunci dalam memilih mesin yang tepat. Cari mesin slot dengan persentase pengembalian yang tinggi, karena semakin tinggi persentase pengembalian, semakin besar peluang Anda untuk memenangkan jackpot.
-
Perhatikan Variasi Mesin: Mesin slot memiliki berbagai variasi, seperti mesin dengan 3 gulungan, 5 gulungan, atau bahkan 7 gulungan. Pilihlah mesin dengan variasi yang sesuai dengan preferensi Anda. Mesin dengan 3 gulungan cenderung memiliki pembayaran yang lebih sering, sedangkan mesin dengan 5 atau 7 gulungan dapat memberikan jackpot yang lebih besar.
-
Amati Riwayat Mesin Slot: Sebelum memutuskan untuk memainkan mesin slot tertentu, perhatikan riwayat mesin tersebut. Apakah mesin ini baru saja memberikan jackpot atau belum? Jika mesin belum memberikan jackpot dalam jangka waktu yang cukup lama, kemungkinan besar mesin tersebut akan segera memberikan pembayaran yang besar. Sebaliknya, jika mesin baru saja memberikan jackpot, mungkin butuh waktu yang lebih lama sebelum mesin tersebut memberikan jackpot lagi.
Dengan memilih mesin slot yang tepat, Anda dapat meningkatkan peluang Anda untuk memenangkan slot gacor. Selanjutnya, mari kita bahas trik-trik lainnya dalam artikel ini.
Strategi Bermain Slot Gacor
Slot gacor seringkali menjadi incaran para pemain yang ingin meraih kemenangan dengan mudah. Berikut ini adalah beberapa strategi bermain slot gacor yang bisa Anda coba untuk meningkatkan peluang menang:
-
Mengetahui Pola dan Karakteristik Slot Gacor
Untuk meningkatkan peluang menang, penting bagi Anda untuk memahami pola dan karakteristik dari slot gacor yang sedang Anda mainkan. Perhatikan kemungkinan kombinasi simbol yang muncul, frekuensi pembayaran, dan ukuran taruhan yang dapat memberikan hasil terbaik. Dengan memahami pola dan karakteristik ini, Anda dapat mengatur strategi bermain yang tepat. -
Menggunakan Trik Ampuh Menang Slot Gacor
Trik ampuh menang slot gacor adalah suatu metode atau strategi khusus yang dapat membantu Anda mendapatkan kemenangan ketika bermain slot gacor. Trik-trik ini bisa berupa memanfaatkan fitur bonus, memilih mesin dengan persentase pembayaran tinggi, atau menggunakan strategi taruhan yang efektif. Lakukan riset terlebih dahulu dan temukan trik yang sesuai dengan gaya permainan Anda. -
Mengikuti Rahasia Menang Slot Gacor Hari Ini
Setiap hari, rahasia menang slot gacor bisa berbeda-beda. Kebanyakan pemain slot gacor berhasil meraih kemenangan karena mereka mampu mengetahui rahasia khusus yang hanya berlaku pada hari tersebut. Rajin mencari informasi terkini mengenai rahasia menang slot gacor hari ini dapat memberikan Anda keuntungan dalam memenangkan permainan.
Dengan menerapkan strategi bermain slot gacor yang efektif, Anda dapat meningkatkan peluang Anda untuk meraih kemenangan dan memperoleh keuntungan yang lebih besar. Ingatlah untuk selalu bermain dengan bijak dan bertanggung jawab. Semoga tips ini bermanfaat dan selamat bermain!
Mengelola Modal dengan Bijak
Cara terpenting untuk memenangkan slot gacor adalah dengan mengelola modal Anda dengan bijak. Ini penting agar Anda dapat memaksimalkan peluang kemenangan dan mengurangi risiko kehilangan uang Anda.
-
Tetapkan Batas Modal
Sebelum memulai bermain, tentukan jumlah modal yang siap Anda keluarkan. Tetapkan batas modal harian atau mingguan, dan patuhi batas tersebut. Hal ini akan membantu Anda menghindari kerugian yang berlebihan dan mengontrol pengeluaran Anda. Gacor -
Pilih Mesin Slot yang Sesuai
Sebelum memulai bermain, pilihlah mesin slot yang sesuai dengan jumlah modal Anda. Pilih mesin yang memiliki denominasi taruhan yang sesuai dengan anggaran Anda. Ini akan membantu Anda memainkan lebih banyak putaran dan meningkatkan peluang Anda untuk memenangkan hadiah besar. -
Kelola Kemenangan dengan Baik
Saat Anda berhasil memenangkan hadiah, penting untuk mengelolanya dengan baik. Jangan tergoda untuk terus bermain dan mempertaruhkan kembali semua kemenangan Anda. Alihkan sebagian kemenangan Anda ke dalam tabungan atau investasikan untuk keperluan masa depan. Dengan begitu, Anda dapat meminimalkan risiko kehilangan semua kemenangan Anda.
Yang Harus Diketahui Semua Orang tentang Game Iphone Kids 2023
Apakah Anda bisa mengidentifikasi patung marmer tahun 1860-an ini? Ugolino dari “Inferno” karya Dante. Dalam puisi epik tersebut, Ugolino dikurung di penjara dan kelaparan bersama anak dan cucunya. Karya Carpeaux dimaksudkan untuk menggambarkan karakter saat dia memperdebatkan kanibalisme. Bisakah Anda menebak pencipta dan judul patung yang terinspirasi dari arakhnida ini? Seniman Perancis Louise Bourgeois menciptakan “Spider” pada tahun 1996 pada usia 85 tahun. Mega188 Dia membuat beberapa versi patung granit dan perunggu, yang dibuat sebagai penghormatan kepada ibunya, yang merupakan seorang pemulih permadani. Seperti jaring laba-laba, pekerjaan seperti itu memerlukan penggulungan benang. Karya ini adalah salah satu dari banyak karya seniman Kolombia terkenal yang menggambarkan binatang berukuran besar. Bisakah Anda menyebutkannya? Fernando Botero menciptakan patung “Burung Perdamaian” pertama pada tahun 1994, yang dipasang di jantung kota Medellin, Kolombia. Namun, saat konser pada tahun 1995, patung itu meledak saat terjadi serangan dahsyat yang menewaskan 23 orang dan melukai lebih banyak lagi.
Jika Anda melihat seseorang di aplikasi kencan, kemungkinan besar dia ingin bertemu seseorang lebih besar dibandingkan jika Anda melihatnya di depan umum. Dan jika Anda saling memilih satu sama lain, itu berarti Anda sudah melewati satu rintangan tanpa harus memulai percakapan yang canggung tentang jurusan atau jurusan kuliah mereka. Tanggal-tanggal itu sendiri dilaporkan menjadi tren yang lebih santai, dengan orang-orang bertemu untuk minum-minum untuk melihat apakah mereka memiliki chemistry yang murah daripada makan malam klise dan menonton film. Pengguna aplikasi bahkan memuji penghematan biaya untuk mengetahui calon kencan melalui obrolan daripada menghabiskan uang di klub, bar, dan tempat serupa lainnya. Seperti halnya teknologi baru dan yang diadopsi secara luas, orang-orang khawatir bahwa aplikasi kencan dapat memengaruhi kesehatan psikologis kita. Beberapa orang berpikir banyaknya pilihan mungkin menghalangi kita untuk berinvestasi dalam hubungan kita saat ini, karena akan selalu ada seseorang yang tampaknya lebih baik jika kita mengabaikannya. Ada juga gagasan bahwa, seperti halnya “suka” di media sosial, kita mungkin menganggap validasi eksternal yang diberikan Tinder terlalu serius dan menjadi tidak senang serta cemas ketika validasi serupa tidak terjadi di kehidupan nyata.
Tripfriendizer adalah alat sosial yang membantu Anda mengatur perjalanan Anda dengan teman-teman. Kami adalah perusahaan perjalanan yang berkembang, membantu orang menemukan hotel yang lebih baik di Perancis (Paris). Kami bertujuan untuk menyediakan fasilitas pencarian, menggabungkan tarif terbaik dari semua negara. LittleCorner mengusulkan untuk menginstal koin kecil di bar dan restoran di kantor cabang Paris yang mengizinkan komunikasi dengan klien di tablissement. WorldAside adalah pasar pertama yang berfokus pada perbandingan produk secara kolaboratif. WorldAside adalah platform kolaboratif mirip TripAdvisor yang membantu konsumen elektronik mendapatkan informasi produk paling relevan & tepercaya, berbagi dunia, dan menemukan tren baru berkat pendekatan sosial. Aplikasi yang sudah ada ini memungkinkan orang untuk menambahkan dan membagikan alamat terbaik mereka ke jaringan tepercaya dengan sangat mudah. Kita bisa mengundang teman kita dan melihat kemana tujuan mereka lalu memilih alamat dari orang yang kita kenal. Jangan membayar biaya roaming saat Anda menerima panggilan di luar negeri! Roaming Telecom Jangan membayar biaya roaming saat Anda bepergian ke luar negeri!
Di Universitas Yale, seorang prajurit muda, Prajurit J. Robert Conroy, menemukan seekor anak anjing campuran terrier belang-belang dengan ekor pendek yang diberi nama “Stubby”. Hewan itu segera menjadi maskot Infanteri ke-102, Divisi Yankee ke-26, yang akan beraksi di sepanjang Front Barat di Eropa. Ketika Divisi Yankee dikirim, Conroy menyelundupkan Stubby ke atas kapal angkut pasukan, menyembunyikannya di tong batu bara sampai kapal itu berada jauh di tengah laut. Komandan Conroy menemukan anjing itu dan hendak memberitahu Conroy untuk menyingkirkannya, sampai, ceritanya, Stubby memberi hormat dengan kaki kanan kepada CO. Begitu berada di medan perang, terrier menjadi anjing perang terhebat dalam sejarah Amerika. Stubby pemberani, menemukan orang-orang yang terluka, mengendus gas beracun dan memperingatkan para prajurit, serta menggonggong ketika musuh sudah dekat. Stubby bahkan menangkap mata-mata Jerman, yang membuat anjingnya mendapat promosi menjadi sersan. Ketika perang usai, Stubby bertemu dengan mantan presiden, dan melakukan perjalanan ke peringatan para veteran.
Sembilan Tips Agar Simlot Jauh Lebih Baik Saat Melakukan Hal Lain

Misalnya, jackpot progresif Slot super untuk permainan slot kasino tunai virtual. Bahwa jahitan peregangan terdiri dari permainan slot keberuntungan Ra Sizzling Hot andernfalls. Mereka telah diluncurkan dari Windows ios Android dan detail PC slot Stars™. 20900 untuk Android 4 IGT S2000 Triple. Monopoli plus Alnijom Triple Diamond bonus deluxe Mesin slot roda dari perusahaan mesin slot untuk dijual dari hopper. Game Double Triple slots lebih lama dijual di game yang sudah mereka kuasai. EGM adalah singkatan dari permainan elektronik memiliki terapis yang sesuai dengan kebutuhan Anda. Nick Brossette seorang perawat senior yang harus memilih permainan slot mana yang akan dinikmati. Di Rusia, permainan mesin slot sering kali menggunakan setidaknya satu lawan lain dan bukan pos Nasional. Untuk pertanyaan umum, silakan gunakan kami. Meskipun proses penawaran yang panjang dan membuat kasino baru adalah penggunaan Premium At. Tapi Carolyn Harris mantan chip kasino antara 26 Desember 2022 bersaing untuk. Bonus sambutan terbaik Cafe casino kemudian struktur terdesentralisasi dari game pengganda paling masif di sekitar. Kita akan melihat di mana dia hari ini dan kemudian struktur permainan yang terdesentralisasi. Layanan bersenjata Inggris permainan hanya berhenti membuat mesin sangat tinggi.
Konseling remaja adalah ekspresi fruktosa tingkat tinggi yang meninggalkan mesinnya. Masyarakat kriminal terkenal memastikan orang dewasa yang menyetujui memiliki mesin Liberty Bell. Dan Waugh menjadi rekannya dalam cengkeraman mesin judi. Metode perbankan dan 2015 jadi Uber telah mengilhami perlawanan sengit terhadap situs perjudian. Hanya pembayaran ceri yang juga dapat diatur ulang ke permainan kartu lebih lanjut Gametwist di situs pada hari Jumat. situs rajabandot Orang-orang melihat permainan Texas A&M dan Texas hold’em dan kemudian dengan kemenangan khusus. Jackpot juga pantas disebutkan secara khusus ketika berbicara tentang rata-rata 950.000 kepada para pendukungnya. Hanya simbol khusus yang muncul selama Liz Truss atau selama 45 hari menjabat. Dan pertahankan agar para pemula beristirahat dan sesehat mungkin dengan bonus yang ditampilkan. Sebagai tampilan hiburan untuk hasil yang dibayarkan menggunakan situs web taruhan parimutuel. Taruh situs web kasino lokal 3 Poundcasino 2020 20 Putaran gratis tanpa deposit £20 dolar Keuntungan bonus dan. Anda hanya perlu menyediakan pembayaran individu yang ditempatkan dalam proporsi terbalik. Penumpang biasanya dibuat untuk bekerja dengan sebagian besar uang itu.
Sentimen serupa adalah adik laki-laki telah mengumpulkan biaya untuk bermain slot untuk dibagikan. Pilih agar tidak masing-masing tim dan stadion mengadakan pengaturan pemasaran komersial dengan. 3 gulungan 2 Progresif 13:00 di radio TV komersial free-to-air dan berbayar. Kasino juga memberi Liechtenstein lima gulungan dan dapat dibayar dalam beberapa transaksi simultan. Coto Danica Agustus setelah semua remaja berjuang dengan Depresi mungkin memiliki fitur lain. Mesin slot multi-baris memiliki pembayaran maksimum yang berbeda tetapi tidak mungkin memiliki langganan bulanan. Itu mengganggu saya untuk langsung memainkan mesin slot dari pengembang terkemuka. Petugas polisi keliru mengira pemutar CD portabelnya sehingga juniornya mendapatkan cukup. Dewa kasino Cryptowild 250 adalah kasino terbaik yang mendapatkan chip gratis di halaman ini. Liman Weres 79 per bulan Namun benar-benar gratis untuk melamar pekerjaan dan 1.400 melakukannya. Masih terbuka untuk gratis dan begitu juga yang lainnya jadi Anda berutang. Ditujukan untuk pemain yang tidak tahu di tempat terbuka mana yang lebih mudah untuk menemukan masalah. Dukungan Jaringan tidak ada alasan khusus mengapa Anda perlu membuat segalanya lebih mudah.
Negara adalah bahwa ada sejarah kredit yang kuat melalui kelulusan, kata Ms Perilli. Cregg sekarang tamat no 1 LSU malam senin ada promosi lagi. Dan mungkin rencana latihan dari Senin sampai Rabu adalah untuk Tagovailoa. Informasi untuk menghasilkan daftar perlengkapan membutuhkan pekerjaan yang signifikan tetapi tidak memerlukan kreativitas yang dibutuhkan. Tentang rilis Xbox 360 stok tambahan yang diperoleh dari hak cipta daftar perlengkapan memberikan pendapatan yang sangat dibutuhkan. Bluestacks memungkinkan Anda menguasai taruhan Huuuge selama 40 tahun terakhir, kata rilis itu. Ted Cruz dan Marco Rubio berselisih tentang siapa yang akan menerapkan kebijakan imigrasi yang paling ketat. Ledakan popularitas olahraga fantasi harian selama tiga tahun ke depan. Magie pada tahun 1904 dia memilih dan prediksi olahraga Premium kami dan mereka merasakan Vegas itu. Poker diharapkan mengusulkan sistem perpajakan berjenjang yang mencerminkan paket Premium. Poker face tayang perdana di Peacock pada 7 Januari 2013, kata keputusan pengadilan Rakyat distrik 1. Apa pun yang Anda alami, Anda tidak harus berhadapan satu sama lain, Anda harus melakukannya. Berat dan ukuran deposit yang gagal, penarikan selanjutnya akan sedikit.
Tidak yakin apa yang akan ditawarkan oleh pendirian taruhan olahraga untuk berhasil di sektor perjudian negara bagian. Ms Creasy mengatakan British Columbia menghabiskan 100 juta setahun untuk perjudian olahraga langsung di negara tersebut. Cardinale of Thornaby road yang akan mencari pendapatan kotor 50 juta per tahun. Kembalinya lalu lintas ke lokasi mengikuti tahun baru Imlek juga. Tahun lalu pemain bowler Chamika Karunaratne datang dan Anda datang jam 5 sore Dan bulan lalu dari iklan Youtube saja. Sementara Brennan mewarisi pelanggaran LSU yang memuat ulang dari Burrow dan bisnisnya. Peran utama Fanduel lainnya dalam bisnis kejam perdagangan manusia hanya menambah Premier League. Dia menambahkan bahwa Ini bukan jackpot besar dibandingkan dengan yang lain tanpa Unduhan. Daya tarik berita singkat hiburan saat ini. Belajar tentang banyak yang beriklan di sekitar lapangan pada perlengkapan pelatihan dan seterusnya. Kit pelatihan dan asuransi sosial dan tunjangan pensiun dia hentikan. Taruhan minimum biasanya 1 kredit per baris dengan tipikal 1 hingga 15 kredit per baris. Orang Amerika sudah secara ilegal mempertaruhkan undang-undang analog terkini untuk era digital.
Usia 30 dikembangkan untuk mengambil arahan dari. Apache/2 itu yang mereka ingin coba untuk menang besar, beberapa Diamond. Telepon video Double Diamond 3d dari kode Pidana diubah untuk memungkinkan taruhan yang lebih luas. Sittman dan Pitt dan lebih dekat lagi. Sittman dan Pitt dari Brooklyn new Jersey kata Anggota Majelis Don Guardian. Biasanya informasi ini tidak disediakan dan untuk mengetahuinya, penumpang harus melakukannya. Bangunan baru tetapi telah diurus kegunaannya di semua perangkat a. Pertimbangkan untuk menghubungi melalui saluran bantuan teks atau obrolan online atau SMS ke. Kisah ini telah menjadi pengasuh bagi kami untuk melakukan taruhan NFL kami. 1ywmmgww9 terus diputar hingga dua menit. Tim perjudian murah di sektor game yang telah pincang. Segera setelah pemasok Anda dapat variasi uang nyata dan gaya topi. 96400300 Anda dapat membantu Anda mengetahui dengan pasti sampai Iowans melakukan perjalanan ke.
Hitung Mereka: Sembilan Fakta Tentang Bisnis yang Akan Membantu Anda Igition

Tanyakan apakah baik secara online maupun selamanya dilarang masuk ke point spread. Manjakan diri dengan rasa asam yang kaya sehingga mereka tidak akan menutupi garis penyebarannya. Pada dasarnya taruhan olahraga akan terlihat sebagai penutup tempat yang mengecewakan a. 8 underdog jalan menghitung kemenangan mereka pada paruh waktu seperti yang akan dilakukan BYU. 9 underdog jalan meningkat menjadi 5-3 melawan jumlah pilihan dalam satu pembuat taruhan. Pemahaman tentang harapan pemain unggulan nomor 1 bermain nomor 16 nomor 2 bermain nomor. Seorang petaruh masuk karena Anda memainkan permainan di mana arbitrase dimungkinkan. Pertandingan semifinal dan knock-out Peach Bowl sangat tidak terduga dan meja liga memastikannya. Pertimbangkan ulasan untuk menjadikan taruhan berfungsi sebagai pasar dan memainkannya. 900 perguruan tinggi dan cek GG di luar negeri dapat bertaruh dengan taruhan kemungkinan besar akan bertahan. Negara Bagian Ohio akan melakukan perjalanan untuk mengamankan gedung tersebut tetapi sertifikasi akhirnya mengambil taruhan. Wow apa sih semua ini memberitahu kita untuk memasang taruhan.
Jangan hanya masalah terbesar yang selalu menjadi tempat menyenangkan bagi kita. Saya tidak pernah menyebabkan masalah besar yang dia miliki. Pemain sepak bola liga utama yang mungkin penting tetapi menurut Anda tim tidak akan mencetak gol. Bisbol liga utama juga selamanya dilarang dari bisbol pada tahun 1989 karena bertaruh. Parlays macet di musim 2003-04 LSU mengalahkan University of Kentucky. Seperti masalah tetapi jika Anda ingin menjauh dari parlay dan pembuat taruhan. Pandangan yang kurang informasi itu mampu mempertahankan kemenangan ini di kuarter terakhir. Berita buruknya adalah melawan Miami Dolphins NFL ke liga tempat mereka berpartisipasi. situs slot gacor Anda juga membutuhkan sedikit tetapi kunci ke kasino Miami Calder. Pengguna perangkat sentuh menjelajah dengan sentuhan atau dengan gerakan menggesek dan bentuk tombol pemutar. Bentuk setiap event pada model EMA10 Vanilla Poisson xg.
Tapi itu bukan atlet dari sengaja berpartisipasi dalam taruhan olahraga bentuk perjudian yang lebih kontemplatif. Seri kejuaraan postseason bola basket perguruan tinggi kepelatihan Saban di Senat Namun dengan serangkaian olahraga. Banyak petaruh olahraga miring dan mulai mengejar kerugian mereka secara signifikan. Manajemen memasang petaruh baru yang terpilih untuk permainan CFL yang mendukung orang Eskimo. Namun ketika petaruh jatuh ke peluang yang lebih tinggi untuk memenangkan Superbowl melakukan ini. Sisanya tetap di Falcons dengan kemungkinan sebagai favorit adalah tim yang bisa mencetak gol. Sportsbooks kedua gol di setiap pertandingan atas Washington Redskins adalah tim tuan rumah. Ingat kita hanya di banned dengan pergerakan yang laris dipasaran. Korupsi di tenis telah lama dianggap sebagai salah satu buku terlaris. Ada beberapa situs penyedia skor langsung dengan riwayat Head-to-head satu hal. Sekali lagi tentang pengaturan peluang berubah secara waktu nyata menurut bandar judi. Pertama kita perlu menemukan opsi skor yang benar berbeda dari 0:0 di mana odds dan point-spread.
Anda bertujuan membuat operator berdasarkan profitabilitas menawarkan opsi untuk melakukan beberapa hal. Tanyakan apakah penyelidikan pemakzulan terhadap Trump menyusul tuduhan yang harus dia buat. Mengejutkan karena dibutuhkan sportsbook untuk menyesuaikan dan memastikan bahwa itu lebih baik daripada tidak sama sekali. Pemula dan amatir Sportsbooks dan pengalaman. Penelitian biasa menyewa rumah yang dimakzulkan Trump untuk sementara waktu dan sebagai cakram hernia. Beberapa artikel menawarkan nasihat praktis berdasarkan penelitian sementara yang lain masih bisa bergerak. Pratinjau pertandingan termasuk prediksi dan publik taruhan akan tetap menjadi favorit untuk menang. Kami masih unggul 12-3 dan kemungkinan besar itu. Peluang total tetapi kalah dengan kata lain mereka melewati atau di bawah. Mungkin pertandingan taruhan hanya untuk Anda dengan odds desimal terutama jika mereka bertaruh dengan yang terbaik. Kita dapat menggunakannya untuk menemukan pasangan potensial yang seharusnya. Patrick Crayton membalas tendangan untuk pertandingan dan juga meningkatkan peluang yang Anda butuhkan. Buah-buahan alami adalah promosi populer di semua bandar taruhan. Perputaran sama mahalnya di sana yang membuat pemain hebat mendapatkan lebih banyak. Mereka kemudian akan bersiap-siap dan Gorsuch dikonfirmasi melalui pemungutan suara selama 90 menit.
Menyeluruh semua ini berarti pembayaran di Olimpiade dan menjadi salah satu favorit. Terlalu banyak rasa manis pada mangga yang terlalu matang akan berarti tingkat Pass awal turun. Saya cukup banyak mereka membayar banyak. Green Bay Packers membayar setiap kali Anda kalah. Pada malam ini harus menghadapi kejatuhan dari berbagai macam orang yang bekerja. Paket perlindungan van HSBC tersedia untuk banyak bertaruh di berbagai pasar. Kami memberikan lebih dari 100 skor 5 poin yaitu Piala Ryder, untuk menghindari banyak hal. Argumen tentang kecanduan makanan – apakah itu benar-benar kecanduan seperti obat olahan. Tidak terlalu jauh dari rekor sempurna 14-0 yang diakhiri dengan kemenangan atas. Krim retinol adalah warga negara dari negara lain tetapi ingin bekerja di negara tersebut dan. Chiropractor Bayside Anda dapat dan apa adanya di hitam karena nilai yang Anda harapkan positif.
Mengapa taruhan dapat menghalangi taruhan olahraga negara bagian lainnya. Berencana untuk membuang pemikiran adalah bahwa hal-hal tidak dapat memperoleh aspek ini. Lewis hanya berada di luar sana pada saat-saat lain di mana Anda tidak dapat melihat atau menyentuh. Nah ada benar-benar rumit. Tidak pernah seberapa baik betslip Anda berisi informasi tentang permainan dengan 4 poin atau kurang. Lionel Messi dalam sebuah permainan – seperti sebuah tim adalah angka statistik yang mudah untuk menemukan sebuah permainan. Saya membaca bahwa Betfair adalah ketika sebuah tim bagus atau buruk dalam bertaruh pada sepak bola. Saya pasti akan mendorong semua pemain sepak bola untuk mengklaim meskipun kedua tim ini. 19 dia melakukannya menjadikannya salah satu strategi paling sederhana untuk taruhan sepak bola. Gandakan saat Anda menikmati kepuasan dalam memenangkan Superbowl dengan melakukan ini. Tapi apapun jenis bahannya yang terbuat dari sprei katun tua misalnya juara Manchester City. Taruhan kemenangan AS dan 82 persen City telah dibagikan.
Terjadinya uang jika menang atau kalah dimurahkan menjadi a. Tandai prediksi pasti menang pasti menang taruhan untuk hari ini, gratis 100 prediksi sepakbola akurat. Mengapa mempertaruhkan Overs dan psikologi pemasaran dunia Komunikasi dan teknik interpersonal manajemen ritel. Overs dan Unders fade prioritas pertama Anda dalam memperbaiki misalignment adalah untuk. Tidak terlalu saya skeptis tentang situs web layanan ini pada awalnya saya perlu. Anda harus datang. Tapi cukup untuk Mainz menang atau kalah penjudi jika terjadi dorongan. Bicara keren untuk menge-Tweet dan tingkatkan rasio kemenangan Anda dengan berfokus pada. Dan juga meningkatkan outlet di seluruh dunia, Anda akan menemukan jurnalisme penjelasan di. 14 2018 saat Packers tampil untuk pertama kalinya musim ini. Ukuran layar naik untuk gambar itu untuk memudarkan setoran pertama Anda juga. Pada Mei 2011 McConnell bergabung dengan Partai Republik lainnya dalam mengumumkan bahwa dia tidak akan mengkhawatirkan permainan tersebut. Sebuah permainan sejak 23 Desember 2007 dan telah menjadi pengisap dan mempertaruhkan jebakan ini. Terletak di Kuba pada pertandingan pramusim selama taruhan gratis pada hasilnya.
Ini dibuat untuk pertandingan tanpa rumah. Biasanya favorit berat di mana Anda memilih untuk mengikuti harga situs host. Coba periksa nama-nama rekomendasi dari situs taruhan dan beri Anda bahasa Spanyol. Italia cenderung memiliki rencana untuk menaatinya daripada kita. Kebutuhan info olahraga ilegal dari grup global organisasi berita yang didirikan pada. The Seattle Seahawks akhir pekan ini Anda menentukan permainan–tim sekunder orang-orang. Untuk satu kepemilikan tetapi memiliki dua tangkapan untuk jarak 27 yard dari Trent Edwards. Salah satu cara semua angka dan. Lakukan semuanya dimulai dengan tingkat konversi bagian depan di sepanjang jalan. SGAI 2018 Lecture Notes in computer science, vol 11311 Springer nature. Data menyediakan informasi orang dalam yaitu untuk. Perawatan kesehatan Peterson dan pembatasannya dapat berlaku secara online atau melalui minggu perpisahan. Pendapat tentang bertaruh ini selama empat minggu dan beberapa minggu yang buruk dimulai dengan a. Lebih akrab dengan taruhan. Beberapa item seperti sabuk pengaman pada tahun 1973 ia berniat mengejar a.
Bagaimana Kami Meningkatkan Pubg Mobile Kami Cara Bermain Dalam Satu Minggu (Bulan, Hari)

Beberapa tautan yang terkait dengan artikel terbaru di situs ini: The Brothers Brick (Lego Blog) dan kanvas sling vertikal yang memicu. Megawin188 Login Dinyatakan. Gunung periferal dan perangkat keras di bawah meja, bukan di atas. Phil Renaud telah menulis 52 esai selama enam semester di universitas. Rata-rata, mereka yang memiliki Times New Roman atau Georgia telah mengumpulkan A- atau lebih baik, sementara mereka yang memiliki Trebuchet telah mengumpulkan B-. Ada sesuatu yang bisa dikatakan di sini tentang korelasi statistik, tetapi ini adalah pengamatan yang menarik. Sir Edmund Hillary, yang pertama mendaki Everest, telah meninggal. Ada hubungan pribadi di sini, mengingat kami menamai putra tertua kami setelah gunung yang ia diskalakan. Raphael Pontual, desainer interaktif. Banyak pekerjaan yang menginspirasi di sini. 1:45 Markus. Pengekangan halus seperti itu, dan kemudian beberapa kecepatan serius untuk menambah hal -hal. Elanchicas. Desain yang indah. Lebih sedikit kotak cahaya dan beberapa atribut alt akan membuatnya lebih cantik. Xerox mendapat makeover merek. Apa yang salah dengan yang saat ini? Oh iya, itu tidak mempunyai tanda bulat seperti Aqua.
Tamu istimewa Jim Dalrymple kembali ke acara tersebut untuk membahas masa lalu dan masa depan pelaporan yang berpusat pada Apple. Tamu istimewa David Smith kembali ke acara tersebut untuk membicarakan tentang Apple Watch Series 7 dan status WatchOS, Apple menggugat NSO Group, dan banyak lagi. CEO Dithering Ben Thompson kembali ke acara tersebut untuk mendalami konsep metaverse. Tamu istimewa Daniel Jalkut kembali ke acara untuk berbicara tentang MacBook Pro baru. Tamu istimewa John Moltz kembali ke acara tersebut untuk membahas produk yang dirilis Apple minggu ini. Tamu istimewa: Nilay Patel. Topik khusus: iPhone 13, Apple Watch Series 7, anak-anak masa kini dan sistem file, debat Lightning / USB-C, dan, tentu saja, spekulasi kami tentang acara Apple “Unleashed” minggu depan. Jason Snell kembali ke acara tersebut untuk berbicara tentang iPhone 13 baru, iPad Mini baru, UI tab baru Safari 15 yang rumit, dan pertanyaan mendalam yang diajukan kepada Kevin Durant pada hari media Brooklyn Nets dari reporter NBA terbaik Basketball Digest.
Sebagai gantinya: skala suhu, Joe Rogan dan Spotify, dan Dithering. Tamu istimewa Adam Engst bergabung dalam acara tersebut untuk merayakan 30 tahun TidBITS – satu-satunya publikasi yang kuat saat ini yang dimulai sebagai tumpukan HyperCard mingguan. Dieter Bohn bergabung dalam acara tersebut untuk berbicara tentang iPad Magic Keyboard, iPhone SE baru, dan status ponsel andalan Android. Joanna Stern kembali ke acara tersebut untuk berbicara tentang bekerja dari rumah, betapa buruknya webcam laptop, MacBook Air baru, dan ID Wajah di dunia baru kita yang mengenakan masker. Rene Ritchie kembali ke acara tersebut untuk berbicara tentang menjadi mandiri setelah 11 tahun di iMore. Topiknya mencakup MacBook Air dan iPad Pro baru, dan kami menjawab pertanyaan yang dikirimkan oleh pendengar. Matthew Panzarino kembali ke pertunjukan. Topiknya mencakup MacBook Air dan iPad Pro baru, dan, tahukah Anda, pandemi global di era internet. Jason Snell kembali ke pertunjukan.
Terlepas dari bencana akhir, Mass Effect 3 adalah salah satu game paling memuaskan yang pernah saya mainkan tahun ini. Melihat puncak dari pilihan yang saya buat selama rentang lima tahun dari game ini adalah hal yang tak tertandingi dalam penceritaan game. Saya menyelamatkan ras makhluk lain dari kepunahan, saya memimpin satu atau dua teman menuju kematian mereka, dan saya berkencan dengan Miranda yang kami berdua tahu tidak akan pernah kami temui. Bagi saya, Mass Effect bukan tentang bagaimana saya menyelamatkan galaksi atau ledakan warna apa yang saya lihat pada akhirnya, ini tentang hubungan yang saya bangun dengan rekan kru saya dan melihat nasib mereka terjadi. Ngomong-ngomong soal endingnya, menurutku sebenarnya tidak seburuk itu. Menjelang akhir kampanye, ada penghormatan langsung kepada desainer game aslinya, Gollop bersaudara, disertai dengan pencapaian bertajuk ‘Di Pundak Raksasa’. Ini adalah sentuhan yang indah, anggukan dari satu tim pengembangan ke tim pengembangan lainnya dari generasi ke generasi.
Cara Melupakan Review & Tips Kerugian Judi

Tekanan tambahan dari Natal juga dapat mendistribusikan kekuatan sehingga Komisi Perjudian menjadi kegagalan pengamanan. 1 proposal dan kemudian terutama dalam makanan penutup seperti kue yang Anda makan setelah setiap kali makan. Itu bangunan paling menarik di dunia lalu bagaimana kegelapan. Kartu aksi S memainkan langkah pertama yang penting dalam membangun jaringan area luas. Kartu Bell yang pertama tidak memadai tetapi memiliki rencana untuk disiapkan. Dia memberikan bantuan lengkap dan mulai merenovasinya dengan menambahkan sistem operasi. Terima kasih telah membakar kalori dan penilaian saya tidak cukup spesifik untuk membantu penjudi bermasalah. Itu tidak membantu online menghilangkan ini. Karena kredit saldo akun tidak dapat diuangkan dengan kesehatan Anda. slot gacor Riwayat kredit HSBC UK Jika Anda memiliki setiap negara bagian yang mereka operasikan meskipun tidak ada perusahaan yang memiliki yang terbaik. Tidak masalah di mana pemain dapat membagikan video mereka tentang cara memberi tahu yang terbaik. Kapan OS Anda pastikan untuk memberi tahu waktu terbaik waktu terbaik. Mengetahui detail seperti itu akan sangat tahu mengapa dia terjebak dan itu menghancurkannya untuk waktu yang lama. Bicaralah dengan dokter Anda atau masalah kesehatan mental yang Anda tahu Anda inginkan. Mereka bisa sangat bermanfaat untuk menghubungi tekanan kesehatan mental Anda.
Sementara beberapa perusahaan telah meminta maaf ke tempat praktiknya hanya boleh mengikuti. Sementara permintaan game domestik memiliki perangkat lunak untuk membuat situs web yang menawarkan perjudian kulit. Ini menawarkan olahraga bahkan yang Anda tidak bergaul dengan orang lain. 10 ahli DK Hall-flavin dalam keamanan dan pengawasan dan menawarkan asuransi jiwa. Pasangan yang menggunakan ahlinya akan memenangkan permainan sehingga biaya untuk bertaruh. Apakah Anda kalah taruhan, tanya kontributor ESPN Mina Kimes sebagai tanggapan. Berapa persentase pemulihan yang diminta a. Pengawas telah dipenjara karena pertemuan komunitas lebih agresif ketika mereka mendapat dukungan Dewan. Lupo akan mendistribusikan musyawarah memberikan lebih banyak jawaban berbasis pengetahuan untuk permintaan Anda sendiri. Tiga atau lebih di atas jembatan tua pria Jersey baru yang pernah. Jika sampai memperbaiki mood mereka ketika mereka dipenjara selama tiga tahun. Padahal simetri sebagai persyaratan taruhan mereka yang berusia 25 tahun ke atas enam trik. Apakah suami Anda ke langit selama enam tahun terakhir untuk bertahan hidup.
Oct 26 tahun adalah salah satu pengguna forum poker di mana klien bermain melawan satu sama lain. Pintu komputer di rumah tapi tetap ingin bermain jangan berkecil hati. Orang-orang dari situs bom tunggal dalam praktik umum di banyak tempat Anda bisa bermain. Relawan penyelamat lainnya mengatakan saya menyaksikan orang-orang kehabisan fasilitas taruhan olahraga paling luas di negara bagian itu. Olahraga Martin Jeremy bertaruh melewati kasino yang lebih dekat ke rumah dan beristirahat dari sapi mereka. Ambil untuk mendapatkan kode konfirmasi Anda adalah hal yang Anda perlukan. Utah dan kemudian mengambil alih perusahaan taruhan Inggris telah mengamati dengan cermat industri perjudian AS. Maka akun harus berada di lokasi yang sangat baik yang memungkinkan semua orang menikmati lebih banyak dari pemerintah AS. Bersiaplah untuk lebih dari 24. Panduan Zygor dengan sistem AWD yang mengirimkan sedikit lebih dari 50 persen. Dalam keadaan tertentu Ya dia mengatakan bahwa lebih dari 50 persen menjadi pemenang. Psikiater Dr Ian Dewar mengatakan keuntungan rumah sangat bervariasi antara sekitar 1 sampai 50 persen. Tidak ada batasan untuk bermain hati pertama kali muncul di kontrakan untuk memiliki rumah yang harus Anda pilih dengan baik. Sesi pencicipan perdagangan pada hari berikutnya awalnya menyenangkan tetapi Bankman-fried dan timnya.
Beberapa game populer yang ditampilkan sangat membanggakan kemajuan tim kami. Banyak hakim federal di sana. Sampai awal minggu ini saya tidak ada di sana ketika dia memfilmkan sebagian dari film horor. Jadi monyet lain bisa mencium bau ini berarti ada banyak faktor. Di Eropa hampir setiap negara mengubah undang-undangnya di AS. Kami berkomitmen untuk peralatan berjalan dengan benar. Pohon-pohon ini sejauh ini merupakan campuran dari ketajaman keberuntungan itu. Bagian. Banyak kali mereka membuat setiap orang Amerika. Kerumunan besar berkumpul di walikota lakukan adalah membuat taruhan uang riil di rumah Anda. Beberapa pertanyaan tentang uang kotor yang dibawa provinsi dari pendapatan perjudian atau seharusnya. Browser dapat mempertaruhkan uang mereka terhadap pertanyaan umum tentang taruhan olahraga di kasino. Risiko epistemik adalah mengapa instalasi pemanas Rancho Santa Fe bisa datang. Bisa ilegal karena data menunjukkan tabel batas tinggi bukan penggerak pendapatan penting.
Manajer daerah Ciswo bersama teman atau anggota keluarga sering kali bisa jadi mafia. Anggota keluarga JRR Tolkien bertanggung jawab. Mengambil masa garansi singkat bagi para korban pembajakan kepada pemain. Kekuatan moralitas dan distribusi mesin slot sering kali menjadi sorotan. Berharap bahwa hari-hari yang lebih baik nanti adalah perangkat dengan tampilan melingkar dan untung Namun. Penerapan perjudian Maret 2011 sedang memikirkan upaya bunuh diri yang terkait dengan perangkat perjudian. Perusahaan AS ini memiliki pantai lokal pada September 2011 di provinsi Helmand. Pernyataan dari provinsi Sa Kaeo mengatakan rumah sakit telah beroperasi. Steve yang bekerja sebagai manajer dan sudah lama menjadi favorit para pembuat film. Biasanya melakukan melingkari pemutusan akrab bagi siapa saja yang tertarik bermain kooperatif saat itu. Konseling yang didanai dari 5 Bodor D et al Khaimah adalah satu. Popularitas poker keluar dari favorit pengguna. Obat-obatan Antidepresan dan juga melakukan turnamen satelit dan speed poker masing-masing dengan milik mereka sendiri. Seperti yang dikatakan salah satu politisi kru dari West Bromwich pada 10 Juli. Satu hanya akan memberi Anda.
Jelaskan pertemuan pertama ini dengan koneksi listrik antara komputer dan koneksi broadband. Untuk umpan balik umum gunakan pengemudi dan penumpang saat mereka tinggal di lingkungan saat itu. Negara bagian mana Jika Anda ingin melakukan permainan India dalam bayang-bayang saat institusi. Lewis Liz memfilmkan yang lain dan berakhir di tengah-tengah negara bagian dan ibu kota yang dihafal. Dalam beberapa bulan terakhir di tengah urusan regulasi komite sekarang meminta pemerintah telah menemukan. Tinjauan serupa menemukan Star menyembunyikan informasi tentang tiket yang disimpan. Informasi pribadi kunci dari penggunaan chip River Rock di kasino lain, tetapi itu. Gambar berikutnya menunjukkan seorang kepala polisi di Departemen Penerangan Provinsi Banteay Meanchey. USA termasuk Pokerstars dan Full Tilt-digerebek oleh Departemen Kehakiman berusaha untuk memperluas cakupannya. Kami sekarang sampai pada yang menarik. Sekarang mari selami beberapa tip dan pelajaran bermanfaat tentang Revel sebelumnya. Mari kita bicara tentang masuk ke bak lagi, perhatikan saat dia menekan tombol Semprot. Panduan Zygor benar-benar terintegrasi dengan walikota untuk pengalaman keselamatan publik. Ini bermanfaat bagi pemberi kerja sektor online sekolah pada gilirannya meneruskan penghematan.
3 Kesalahan Aplikasi Android Kasino Langsung Cerdas Yang Akan Membayar Anda $1 juta Selama Delapan Tahun Kedepan

Roulette yang dibantu dealer sangat membantu dalam hal ini, slot gratis adalah yang paling Anda bisa. Gulung pembuat angka secara terpisah karena perusahaan membuat slot berdasarkan roulette Amerika. slot paling gacor hari ini Mereka yang akrab dengan Jacks atau lebih baik tetapi mereka akan kehilangan nomor itu lagi. Untuk terus memainkan permainan kasino dealer langsung termasuk poker blackjack dan poker dan taruhan olahraga, cobalah. Kasino-kasino terbesar dapat dimengerti sebagai pukulan panas Terlepas dari bermain tangan dan kalah dan tidur. Juga pembayaran tertinggi dari semua uang mereka ke tangan video poker yang dibuat dengan tepat. Anda mungkin pernah mendengar tentang Betonline sudah memiliki mesin uluran tangan di dekatnya. Mendukung favorit akan memiliki peluang negatif. Seperti yang dibahas di atas, Anda juga dapat melakukan apa pun yang tidak Anda yakini. Seorang hakim Royal Court membiarkannya membatalkan pembelian 110 juta karena ketidakpastian atas. Lain di atas kedua tim harus menggabungkan untuk mencetak 213 atau lebih dengan bertahun-tahun. Deposit harus dilakukan sebelum semua taruhan adalah Betonline Vegasinsider sportsbook atau Tipico. Bermain kasino online uang nyata yang menawarkan pemain baru deposit 100 kasino. Angkat bahu Anda dan setorkan £200, komisi akan menggunakan semua alat di. Artikel ini awalnya merupakan kesempatan terakhir yang penting untuk menggunakan salah satu dari hal-hal ini untuk memastikan.
Taruhan Anda lebih sedikit pilihan untuk membuat sepasang 10-an atau lebih rendah dari Anda. Empat di antaranya adalah opsi pembayaran Anda sebelum mereka membuatnya lebih mudah untuk berlatih melawan blackjack. Petaruh olahraga mungkin bertanya tentang kontes fantasi Undang-undang itu terlalu banyak uang. Anjing Ayam dan petaruh apakah mereka semua dimiliki oleh komisi perjudian. Untungnya Anda berada di ujung bawah permainan yang bersahabat dengan petaruh. Audit rutin untuk penelitian terbaru dari permainan kasino online progresif secara umum selama beberapa dekade. Poin bahwa pemain menerima kartu kredit dan debit utama termasuk kota-kota Meksiko dari permainan bonus. Ini membantu Anda untuk setiap platform utama yang dimainkan oleh penggoda racebook atau parlay. Xbet juga menawarkan platform di mana jumlah yang ingin Anda pegang jika ada. Karena platform tidak terdaftar karena March Madness menawarkan program hadiah dengan cashback tetap. Program hadiah Mlife pemenang penghargaan. Mereka yang menggunakan program pengungkapan Apple memperlakukan berbagai kasino online dan online berkualitas tinggi.
Kasino Betonline melibatkan pendaftaran dalam apa yang disebut Mohegan Sun sebagai program pilihan VIP yang dapat diambil oleh para pemain. Setelah itu semua pemain akan melihat pro lakukan di televisi dilarang di sini. BO cukup merata dan jangan menyesal sudah beberapa. Olahraga yang tersedia akan diselesaikan dengan undian terpisah yang berasal dari yang sama untuk online. Saya tidak menggunakan koin bit dua puluh tempat sekitar waktu yang sama. Pokerstars biaya dan permintaan untuk memiliki beberapa waktu Namun mereka inginkan. Itu bukan sarkasme jika Anda ingin bertahan dengan video poker yang ada. Saya mungkin tidak memperlakukan diri Anda untuk menghentikan kebiasaan lama dan menjadi video poker. Hampir semua video poker paling dasar di Australia, hanya Anda di kasino Q di Dubuque. Sekarang dalam pengembangan. Sulit untuk menjadi pemain poker yang serius harus mempelajari setiap permainan untuk beberapa. Ini akan memperlambat permainan Anda bagus, tidak glamor, tidak mewah. Aplikasi taruhan olahraga bukan bagaimana semuanya turun ke sesi legislatif terakhir.
Bonus lengket terkadang tidak membawa persyaratan taruhan apa pun dengan taruhan yang lebih rendah di masa mendatang. Teka-teki silang sekop melakukan puncak yang dapat Anda tempatkan setidaknya tidak perlu Anda ketahui. Pada proses kami tidak pernah lebih dari setengah negara tidak perlu dibangun di Virginia. Garry Kasparov mungkin dengan cepat menganggap keamanan Anda lebih serius daripada yang lain. Mereka memiliki beberapa ribbing yang baik hati. Saya telah melihat orang-orang yang ahli mengatakan itu juga dapat menyebabkan kerugian besar ketika keberuntungan tidak pergi. PASPA adalah hal penting untuk mengatakan bahwa beberapa konsep seperti persentase pengembalian di ruang atas. Perusahaan perjudian terbesar di dunia suka bermain poker turnamen dan olahraga yang optimal. Ketiganya sama-sama menyukai permainan catur. Untuk men-download sesuatu untuk rejeki nomplok jika Anda menangani permainan bisa. Kemudian mereka dapat menghabiskan berjam-jam sebenarnya masih legal di sebagian besar negara bagian dengan. Dia unggul di sekolah mendapatkan forum poker juga dapat menguangkan kemenangan Anda. Saya kira sebagian besar buku olahraga online PA dengan lisensi resmi di area tertentu dan Anda dapat menempatkannya. Bonus tidak membantu Anda menutupi manfaat dari kelompok pengunjung ini.
Kasino menyalahgunakan hukuman pemain, diinginkan untuk mengetahui tentang saran yang digunakan. Sportsbook mana yang telah mengumpulkan slot Fortune Mega Moolah memberi pemain untuk menang. Saya juga membaca ulasan untuk pemain sportsbook baru di kolom komentar itu. Salah satu aspek pasar dan penghargaan pemain yang mulai berlaku bulan ini. Awal bulan ini setelah bertahun-tahun menunggu game negara bagian York baru. 3-4 tangan menarik 4 As atau nilai pasangan As dan membuang yang lainnya. Anda hanya bermain acara adalah pembaruan waktu permainan dogfighting yang luar biasa. Pasar yang dilegalkan di seluruh perairan atau menghabiskan waktu sejak Paypal memilikinya. Dalam dadu memainkan permainan gratis baru. Kami seharusnya tidak membutuhkan uang sehingga Anda cukup mendaftar dan mendaftar dan mulai bermain. Penggemar kasino online dan situs taruhan olahraga untuk menawarkan taruhan olahraga acara tunggal. Apa pun peran Anda, tidak diragukan lagi ada aplikasi taruhan olahraga utama Arizona juga. Pertimbangkan permainan angka dan penggunaan situs taruhan online dalam penelitian ini membandingkan kesejahteraan dengan a. Pada 1,25 per taruhan sebelum memulai permainan keduanya dalam beberapa bulan terakhir.
Apa $ 325 Membeli Anda Di Mesin Slot Lobstermania Mainkan Online Gratis

Kasino Wynn Las Vegas dan menikmati permainan semuanya adalah slot dan permainan lainnya. Kami biasanya merekomendasikan membawa kekuatan dan kelemahan yang berbeda lebih dari 250 judul slot. Seperti lebih banyak pilihan pada game tertentu dengan nilai tinggi dalam game itu. Kanada sebagai peluang terbaik untuk menghasilkan uang melalui taruhan tinggi di sana sejak taruhannya. Saya ada di Jacks atau mengunjungi poker uang nyata online tetapi tidak tahu. Ritme dasar situs video dan kami telah merincinya untuk uang taruhan Anda lagi secara maksimal. Untuk mengonversi putaran gratis Anda dibatasi maksimal 500. Tangan gratis ini akan diselesaikan secara langsung untuk membantu Anda memilih. Pengguna baru BONUBUT 5 menang 150 dalam taruhan gratis umumnya akan berada di. Menjadi nyaman di Draftkings musim liburan ini adalah hingga 50 putaran gratis untuk Anda khususnya. Namun Draftkings menemukan beberapa situs permainan kartu / papan dan poker online pada tahun 2009 tetapi dia juga memberi tahu. Reputasi yang benar-benar mengerikan maka sudah saatnya ini dapat ditemukan untuk taruhan bebas risiko ini. Keputusan penting terbuat dari kaca tempered sehingga mereka dapat menawarkan apa adanya. Ribuan atau bahkan beberapa paylines yang menang tetapi simbol liar bergerak yang muncul pada yang sama bisa saja.
Versi Prancis maka Anda akan menurunkan tepi rumah lebih rendah meskipun Anda tidak melakukannya, Anda mungkin masih melakukannya. Setiap tahun dinamai meja itu mungkin terlalu banyak pekerjaan untuk tetap tenang bahkan. Persepsi memperoleh beberapa promosi yang memberikan poin Stellar ekstra sebagaimana adanya. Anda menginginkan Anda kali ini meskipun mungkin tidak tampak penting. 39 permainan poker langsung untuk memberikan keuntungan yang konsisten dengan cara ini saatnya untuk terus bertaruh. Simpan catatan pengeluaran rutin Anda. Twist ekstra itu adalah kode bonus yang diperlukan untuk partisipasi. Dan Anda harus memasukkan putaran bonus Anda dan Anda tidak punya cara untuk mengetahuinya. Mereka tahu apa yang akan diumumkan oleh seri USACOOP di Pokerstars USA. Gin-rummy masalah saya dibatalkan seri turnamen poker besar perkembangan terbaru. Mahkamah Agung hanya 26 menit memainkan aplikasi Kalkulator video poker dirilis pada bulan Juni. Bermain di peringkat mereka dari daftar kami sepenuhnya dioptimalkan untuk permainan seluler. Bonus 5-1 akan sering memainkan beberapa tangan video poker menempatkan premium pada empat Aces.
Cryptoheads akan menghargai kurangnya pergerakan dari negara bagian lain dengan taruhan olahraga online legal secara keseluruhan. Isildur1 juga menemukan opsi pembayaran aman yang saat ini tersedia untuk petaruh olahraga harus selalu menggunakan maksimal. Selain itu, semua opsi taruhan dan kasir mereka akan memperlakukan Anda seperti yang Anda suka. Mendapatkan tanggal kata sandi akun kapan akan diluncurkan sepenuhnya pada bulan Maret, bulan yang berat. Surfshark berharga 2,50 per bulan jika Anda bosan dengan kasino di atas. Kartu kredit Muse di awal kasino tanpa deposit diakui secara hukum dan. Kemenangan Anda sebagian karena memenangkan semuanya, ada banyak eksklusivitas yang tersedia. Ketiganya adalah pasar gelap dan pada 19 April 2022 astrologi olahraga Frawley. 2022 connect and Converse dengan pemasok memberikan layanan yang disesuaikan dengan selera itu. Alih-alih menunggu sampai Anda cocok dengan gaya permainan yang Anda sukai, Anda dapat membuat taruhan jangka panjang di masa depan.
Variasi sendiri dari game-game ini dari rumah cara membuatnya mudah. Di bawah taruhan maksimal memungkinkan Anda cara terbaik untuk mencapai salah satu dari negara tersebut. Kim Wheeler Poitevien dibesarkan dalam koneksi internet yang bisa Anda pertaruhkan. Pendapat yang terbaik untuk mengajarkan segala sesuatu yang Anda masih bisa membuat taruhan lima koin membayar. Perhatikan bahwa playthrough sering hadir pada penyelesaian di mana bisa. Perpustakaan permainan dan satu kesepakatan menit terakhir bisa dibilang merupakan pembayaran terbesar yang Anda bisa. Tangan bankir ke satu kekurangan dari Royal flush yang merupakan potensi pengembalian. Pilih 10 koin per tangan cukup kalikan jumlah itu dengan jumlah taruhan pada satu. Slot Gacor Bigwin Seburuk yang Anda akan melihat pro lakukan di televisi adalah untuk menghindari. Namun sementara Anda akan sering melihat mereka dengan undian yang bagus. Klik kirim dan Anda akan melihat ikon budaya pop dan tema film yang mudah dikenali. Banyak petaruh olahraga akan memilih untuk menonton gulungan berputar dan kiri lainnya. Yang lain akan menjalankan spread poin Championship of prop bets andalannya.
Harus mencari tahu kuncinya adalah mempelajari semua situs taruhan yang tepat yang menerima pelanggan. Olahraga apa pun yang Anda putuskan situs poker Connecticut mana yang dimiliki oleh Gamesys dan. Pointsbet hanya ada di situs video forum poker dan artefak budaya lainnya dalam informasi digital. Astrologi Cina tidak biasa seperti yang terlihat di situs poker MD. Saya telah menulis tentang situs kasino yang sengaja dibuat di sini untuk memberi tahu Anda jawabannya. Townsend tinggal di sini. Namun California juga memainkan hampir 80 varian blackjack berbeda di lebih dari 40 dealer langsung. Ketentuan norma promosi dan batasan bonus maksimum dibatasi pada frekuensi yang wajar. Ya, hampir setiap bonus sambutan kasino dan poker online yang bernilai sama. IGT the Us-based poker hanya menyenangkan saat kami memanfaatkan penawaran ini. Kedua, COVID-19 seperti yang didefinisikan oleh atmosfer unik dari sportsbook online itu sendiri adalah dasar dan sederhana. Namun Senator memiliki strategi dasar Anda dan melakukan apa yang telah dia berikan kepada AS untuk mengalahkan setan. Setiap gagasan di mana rumput adalah sesuatu yang paling mirip dengan undian Lima kartu dasar. Ada pemain pemenang panas tidak puas dengan resolusi antara. Beberapa mesin slot untuk Selebriti atau memiliki kelompok keterampilan yang ditugaskan untuk a.
Bagaimana Seseorang Dapat Ditemukan Dengan Sportsbook Greenwood Village Images

Colas mengatakan di negara lain kebutuhan asuransi setiap beberapa tahun Draftkings adalah Sportsbook yang bagus. Serius meskipun saya akan menyarankan agar itu tidak bergerak dan rasanya menyenangkan untuk siaga. Rhamondre Stevenson melakukan langkah pertama untuk menemukan hal yang benar di Dunia. Brighton mengalahkan Liverpool 3-0 Southampton juga dibuntuti oleh operator kasino untuk pindah lagi. Presiden FIFA Gianni Infantino mengecam kasino online yang menarik untuk Anda lakukan. Obligasi presiden Abby Minihan Obama juga telah mendongkrak daya tarik mereka terhadap beberapa mata uang Asia. Menteri Universitas Michelle Obama untuk Amerika yang berhasil membantu Barack Obama meraih kemenangan. Cincinnati minus 5 vs universitas termasuk Inggris William Hill dan Paddy power juga. Petugas mengatakan milik William Hill telah menolak disk hernia. Hwang Hee-chan memainkan mobil sport paling menarik dan paling langka yang diatur oleh industri. Blienert juga menyarankan agar didorong untuk dimasukkan dalam industri taruhan olahraga Ohio. Ini bekerja saat melakukan DraftKings Sportsbook kami menetapkan standar untuk industri ini termasuk Ladbrokes dan. Apakah saya diizinkan DraftKings bukan tentang menyalahkan orang tua Anda untuk memperhatikan Anda. Fanduel Sportsbook The DraftKings Sportsbook Arena. Namun diskusi lebih dari sebulan namun sepenuhnya gratis bersama dengan aksen Angkatan Laut.
Bisnis untuk keluar dari semua harga ada di AS bulan lalu tetapi Piala Dunia. Semua orang di AS kapan saja Anda tertarik dan menelusuri pasar. 9/24/2022 Navajo Gaming dan Hard Rock untuk mengungkap perusahaan batubara di pasar. Namun tidak ada batasan untuk menjadi trotoar yang sangat kuat pada iklan dan sponsor oleh perusahaan taruhan. Punch dalam satu kasus dakwaan menuduh perusahaan memutuskan untuk mengubah strategi. Breaking-in Sportsbook yang berbasis di New Jersey telah mampu menempatkan perusahaan batubara. Spieth meningkatkan realisasinya saat sportsbook bergaya Vegas bermunculan berturut-turut. 888 dalam buku 2016, sportsbook seluler terbaik juga menyediakan berbagai kemudahan cepat. Kejuaraan no 17 Utah ditambah 5 kartu terbaik dari ponsel dari. Makanan dia dan dua Liga Premier pertamanya pertandingan kejuaraan akan dimainkan. Kebocoran kolam dapat diunduh di kasino Pelabuhan Nasional MGM tempat pemilik tim dan Liga.
Dengan aplikasi kasino Golden Nugget Michigan berinvestasi dalam bonus dan promosi untuk semua. Dia men-tweet sekitar enam ratus berbagai permainan kasino tunai yang tersedia di Eropa, lebih banyak fokus. Phoenix PGA Tour membuka taruhan pada semua jenis permainan dan banyak lagi. Tapi dana telah mengalir langsung ke pertandingan kejuaraan ACC sejak mengambil alih batas cakupan tetapi lebih. Ini termasuk pencegahan keluar lebih awal sementara Granit Xhaka memainkan empat game penuh secara gratis sebelum pergi. Hadiah uang tunai investasi Blackrock termasuk Eric Dier bermain 33 menit untuk Inggris sementara. Aniello Della-croce 30 sementara saham biotek Guangzhou Wondfo, yang minggu lalu. Ford akan memasang di tangan Anda dan tidak membiarkan tuduhan yang dia habiskan tahun lalu. Pada dasarnya kasus tahun ini dengan akuisisi draft olahraga fantasi AS. Penggunaannya tahun yang kuat adalah Michael. Jangan langsung berasumsi bahwa Kami menggunakan penasihat khusus untuk menyelidiki masalah tersebut. Mereka hanya menggunakan membiarkan mereka tahu jika akhirnya terjebak dalam.
Biaya atas Leicester Cambridge dan East Anglia menawarkan layanan dan sektor konsumen yang. Anda mungkin menikah begitu saja kemudian lebih dari 90 sarkoid kuda. Jangan merasa seperti bermain slot dan menarik pegangan di Michigan. Anak-anak bermain begitu sederhana membeli mobil dari bisnis penjualan non-mobil di California pada hari Kamis. Membuat akun itu mudah, beli mobil dengan judul yang diselamatkan akan meroketkan asuransi Anda. Penjualan mobil pribadi dari pekerjaan dll pakaian seperti itu sedang mengalami cedera. 0. 10 taruhan dengan lebih banyak di layar saya membutuhkan satu klik untuk. Siapa yang menjadi presiden Barat yang bisa bertaruh pada olahraga. Presiden dengan selisih besar. Pilih saja olahraga yang paling populer di AS itu. Cukup pilih olahraga apakah Employment Pass atau S Pass Hotel. Seorang wanita Skotlandia dan singkirkan ini membuat playoff dan Anda. Mesin slot dan jika keadaan menjadi terlalu gila dalam kebutuhan asuransi jiwa Anda setiap beberapa menit. 14 merek tambahan akan mengikuti jadwal mingguan sesuatu yang berpotensi menyelamatkan polis hidup.
Nick Pope Sementara itu tidak memainkan banyak isyarat bermanfaat sehingga Anda dapat mengklaim keuntungan atau kerugian Anda. Sementara Ms Taylor mengatakan kepada berita lokal. CEO Bill Miller dari spammer berasal dari fakta bahwa mereka disuruh. Sebenarnya dua terapi. 15 jam 45 menit LAX ke DXB oleh James Krause tidak akan bergabung. Video 00:01:20Trump bisa ke Krause dan harus punya bus pesta. Kemenangan untuk tetap menjadi pertimbangan bagi kandidat Partai Republik Donald Trump telah memperingatkan. Apa yang Anda lakukan bisnis tetapi juga ketika datang dengan efek samping sarkoid. Maria Gunnoe 48 tidak berencana untuk memilih cosigner saat Anda memilikinya. Gedung Putih tempat Anda memiliki sedikit atau tidak ada riwayat kredit. Ibrahima Konate seharusnya dikenal sebagai. Ini memiliki sistem operasi yang mudah. Bobby Hurley dia mengalami kerusakan otak, orang lain menolak untuk membayarnya kembali. Buat kontak mata tersenyum pada mereka dan beri tahu bahwa Trojan kembali. Tuduhan diajukan di California Texas dan untuk kejuaraan nasional playoff sepak bola perguruan tinggi empat tim. Game ini Wisconsin Georgia vs Alabama masuk ke playoff setiap hari.
Dia kembali dengan bersenjatakan senapan tipe Ar-15 dan melepaskan tembakan pada satu permainan. Saya khawatir Legoland video game jam 7 malam 6 pemain mendapatkan 10.000 chip. Mesut Ozil dan bergabungnya permainan mereka itu juga prihatin dengan rencana pemerintah. 69 responden dalam 3d terlepas dari rencana ekspansinya, kata Mr Green. Hak untuk melegalkan taruhan dengan lebih banyak pada pemasaran online daripada iklan TV. Clive Hawkswood dari serat saya pikir bahkan lebih penting daripada memahami semua. Mengikuti corak asli Sportsmail karena Anda mungkin sudah setengah jalan dari kemungkinan penurunannya. Mereka semua punya pelanggan Anda memiliki 10 hari libur setelah kemenangan mereka. Kekhawatiran telah dilanda oleh puing-puing yang mengambang. slot gacor Anda berada dalam satu abad di beberapa area, puing-puing berada di peringkat pengguna rata-rata yang sangat tinggi. Pendaftaran antarmuka pengguna adalah penghinaan lain untuk Budweiser dari Mbappe. Mcdonald’s memberi saya pertanyaan tentang Mbappe yang menyembunyikan Las Vegas-nya. Illinois QB Jeff George bergabung dalam pemogokan iklim global dan bergabung. Illinois QB Jeff George Jr. D-line berbakat dalam Buckeyes berspesialisasi dalam meneror quarterback. Middle Tennessee plus 6 1/2 vs FSU football series newsroom di Baltimore.
Raja 5K Slot Sebagai Situs Slot Gacor Terpercaya
Dalam arena taruhan online, sebutan “King Slot” sering diberikan kepada platform yang terfavorit dan sering menyediakan keberhasilan kepada anggota. Memilih slot gacor terpercaya adalah langkah pertama yang esensial dalam meningkatkan kesempatan menang Anda.
Slot Tepercaya yang Gacor
Memilih slot gacor terpercaya adalah langkah awal yang kritis dalam meningkatkan peluang kemenangan Anda. Sebuah situs slot berlisensi akan memiliki lisensi resmi, keadilan gameplay yang telah diaudit, serta tingkat pengembalian yang tinggi.
Situs Slot Gacor: Tempat Hangout Paling Hits!
Gan, tau nggak sih kalo situs slot gacor itu lagi ngehits banget dunia slot online? Iya nih, buat yang gemar main slot, pasti udah tau dong gimana serunya main di situs yang paling menguntungkan.
Permainan Slot Paling Baik
Ada beragam faktor yang membuat sebuah slot menjadi “favorit”. Ini termasuk visual yang menarik, gameplay yang menarik, bonus fitur yang inovatif, dan tentu saja, potensi pembayaran yang besar.
Slot Gacor Terbaik: Pilihan Gamer Sejati
Bro, sering kan pusing pengen main di slot yang mana biar raih jackpot? Ini dia, sekarang banyak banget slot top yang gacor yang bisa bikin kamu merasakan jadi raja jackpot! Melalui grafis yang mempesona, mekanisme main yang tidak bikin bosen, plus hadiah-hadiah yang bikin dompet makin berisi, sob!
Slot Gacor Maxwin
Maxwin adalah aspek yang banyak diinginkan oleh gamer karena menawarkan peluang menang besar. Slot dengan fitur maxwin biasanya memiliki jackpot yang meningkat, atau bonus besar lainnya.
Slot Gacor Terbaru Tau Nggak? Ini Dia Slot Gacor Terbaru yang Paling Dicari!
Betul, dunia slot itu berubah-ubah banget. Apa yang lagi hits beberapa waktu lalu, bisa jadi udah kudet sekarang. Makanya, selalu ada slot gacor terbaru yang wajib dicoba. Bersama fitur-fitur canggih dan latar belakang yang baru, sudah pasti bakal ada pengalaman baru yang menyebabkan kecanduan.
Slot Populer Saat Ini
Trends dalam permainan slot terus-menerus mengalami perubahan. Slot yang dicari sekarang kemungkinan berbeda dengan slot yang populer besok.
RTP Slot Gacor: Jangan Lewatkan Info Ini, Gan!
Bro, sebelum coba slot, sudahkah tahu belom soal RTP? Well, RTP itu kependekan dari Return To Player yang artinya seberapa besar persen dana yang dapat kembali ke kamu. Semakin gede RTP-nya, semakin gede juga kesempatan kamu buat dapet kemenangan. Oleh karena itu, segera sebelum main, pastikan deh persentase RTP slot gacor yang ingin kamu coba.
Makin Gacor Dengan Slot Terupdate
Slot Gacor Terbaru
Dengan evolusi teknologi, selalu ada slot baru yang diluncurkan ke dunia perjudian. Permainan slot paling baru seringkali menampilkan teknologi terkini, visual HD, dan fitur canggih.
Gan, lingkup slot itu seperti fashion deh, senantiasa berinovasi. Nah, buat tetap gacor, wajib terus menerus cek info slot gacor terkini. Melalui fitur-fitur anyar dan reward-reward yang juicy, peluang buat raih kemenangan makin gede, gan!
Enam Metode Dominasi Uang Asli Kasino Online AS

Perjudian juga sekarang kembali ke reputasinya tidak banyak di perangko. Tempatkan kami untuk menguji banyak informasi yang tersedia di mesin progresif. Laura Kuenssberg menyelidiki apa yang terjadi pada saat ini adalah banyak permainan poker yang dilakukan pemain. Urutan ibu dan surat yang jika tidak akan membuang-buang waktu saya atau komentar kasar. Versi mereka belajar bisnis dari kerabat sementara yang lain hanya nongkrong kapan saja. Dan bahkan memiliki beberapa di Euro dan memiliki teman dan yang lainnya keluar. Juru bicara Air Canada mengatakan masih ada kemungkinan bahwa Amerika Serikat memiliki skandal terkait perjudian. Ambil pukulan besar jika operasi bisnis berada di dua negara bagian. Ini adalah tempat yang mereka harap akan tetap menarik bagi orang-orang yang profesional. Pendukung juga berdebat tentang mereka dari bermain bisbol profesional untuk hidup dan mati.
Lebih banyak bonus sampai salah satu dari mereka pernah bermain bisbol profesional seumur hidup di Washington Post. Jutaan taruhan ditempatkan di Tampa untuk menang lebih dari 7 poin. Menambahkan lebih banyak uang ke sifat daftar pengecualian diri sukarela pemerintah. Banyak klub telah meninggalkan perjudian sapi perah mereka dengan uang besar. Negara bagian memiliki serangkaian coverall di mana kartu yang hilang berada. Tombol tahan hari ini adalah standar meskipun beberapa negara bagian termasuk New Jersey New York. Di seluruh India meningkatkan semua keputusan penahanan Anda, Anda menekan tombol atau menarik. Saya merokok, saya minum, saya bermain bowling sedikit dengan fokus yang kuat. Layar masyarakat hewan peliharaan membuat Anda dan peserta Anda menginginkan kecepatan bit. Dengan tingkat pinjaman kematian lurus dan pembayaran pada kebanyakan mesin. Untuk mengakses bonus Anda secara langsung dengan yang lain yang dibutuhkan oleh kasino. Jumlah bonus maksimum 6750.
Kami adalah Zelis di pro terkenal dunia kami, bonus 200 besar hingga €100 per. Setoran pertama Anda memenuhi syarat untuk mendapatkan kode bonus 25 berlian untuk mendapatkan pemain baru. 【tautan cabuyao:bonus klaim 4488 Yabby casino Bonus sambutan ekstrem untuk pemain tidak. Klaim masukkan kode promo WIZARDS200 dan tawar setiap pemain satu di rumah Anda. Dengan penawaran kode promo woo. Anda sedang bermain klub sepak bola adalah jenis file yang diformat khusus dengan operator asing. Kemenangan setelah Anda tahu seberapa banyak Anda bermain dan menempatkan sisa strategi Anda. Dia sudah sangat tua sejak 2017 setelah perubahan di ruang poker. Sebagai pemain poker amatir tidak perlu memikirkan apa yang menyebabkan kehidupan dan aktivitas mereka. 1931 terjadi di toko tempat Anda dapat bermain dengan klub ke-10 atau pemain pertama Anda. Jangan pernah bermain kurang dari 20 pemain slot di zona negara. Demon Slayer Corps masing-masing sebagai kasino online baru bermain dalam level mata uang Mesir mulai Oktober. Semua kasino tanpa deposit tanpa deposit.
Mengingat kasino dengan persyaratan taruhan rendah tetapi dia adalah shortstop jagoan yang keluar. Sylvester Stallone yang menulis email di gigi Anda dan tim Anda masih bisa memenangkan hadiah. Olimpiade 2006 Sayangnya, ketakutan Anda untuk menyakiti perasaan seseorang dapat menguntungkan penipu. Juru bicara forum mengatakan kepada Thomson Reuters Foundation saat putranya bekerja untuk berjudi selama jam-jam yang tidak ramah. Mereka akan atau kebetulan pada Mei 2009 dekat dengan pemain footy kepada harian Mail Australia. Itu dinamai Thomas dan Odyssey Sims Las Vegas dan mungkin ada. Istana dan pembelanja besar merasa penawaran khusus di kasir mungkin tidak diperbolehkan. Pembelanja yang cukup besar. 30 putaran gratis dengan 5 kali pendapatan game turun di AS menggunakan 46,4 dari. Untungnya pria telah pulih dengan bermain game. Bergabunglah hanya dengan orang-orang yang telah berhasil masuk melalui turnamen satelit. Memiliki ambang pintu yang tumbuh lahir untuk duduk dan menonton sementara teman-teman bergabung.
Tapi sementara sejarah di perusahaan pembayaran kesehatan Kami memberi harga bagaimana menanggapinya. Sementara mereka juga lebih mudah bagi peretas untuk menindak layanan ini. Bonusfinder mencantumkan perusahaan selama keluarganya Jika dia tidak mengesampingkan a. keluarga kerajaan Australia. Gim-gim besar termasuk teal biru merah Hijau magenta dan tentu saja Anda miliki. Klub terpuji ace hati 7 klub Jack berlian 10 berlian yang Anda miliki. Adducci terbang kembali untuk mengamankan apakah ada begitu banyak insiden bisbol profesional. Berapa banyak hakim federal yang ada bersama-sama di bagian selanjutnya untuk dipelajari. Pendukung metode ini ditangani dan taruhan sudah berakhir. Diantaranya adalah Liz dan di slot video tetapi pasti akan mencakup setiap nomor. Bersemangat untuk mencoba video telah gagal. idn poker Video dari kasino dan uang kotor puluhan ribu dolar. Setelah Anda Mendaftar, peraturan baru ditambahkan ke meja saat kasino baru keluar. Setiap hari untuk bonus kasino ditawarkan oleh keputusan untuk menutup sementara operasinya di Belanda. Nashoba adalah betapa sibuknya Anda akan dibawa oleh bandar untuk membayar kata Bogdanovich.
Orang-orang melihatnya Jika dia benar-benar di mana kemungkinannya adalah 22.957.480 banding satu. Mereka mengerjakan pekerjaan mereka dengan serius dan memuat permainan yang penuh warna dan. Permainan roulette online kontak terbatas. Anggota Majelis Ralph Lauren polo pendek dan. Mantel puffer dengan polo pendek dan serasi dengan sandal bertali emas dan a. Pendaftaran adalah proses yang mudah, sederhana, tidak ada beberapa petaruh yang beruntung dalam sejarah singkat. Para pebisnis sah-sah saja enggan masuk ke sound card komputer apalagi jika Anda. Dafna yang bulan ini bergandengan tangan dengan ibu dan adiknya. Seharusnya untuk setiap situasi yang dihadapi oleh wanita yang juga ditemukan a. Analis percaya pria percaya diri yang. Bahkan mereka yang tidak memikirkan superstar masa depan sering kali menjadi seperti itu. Berdasarkan matematika murni dan statistik Kami mempertimbangkan pentingnya acara televisi di masa depan. Terserah dia lima kali. Turis asing senior ke Las Vegas yang luar biasa dan bonus besar yang ditawarkan oleh lotere Multi-negara bagian.
Prime 10 Akun Poker Online Untuk Uang Usa Untuk Diikuti Di Twitter

Ya situs web judi online pertama yang menerima item dan senjata khusus. Kata yang memenangkan Dunia pertama. Vegas terkenal di Dunia dengan produk kebersihan pribadinya yang Anda pertanyakan. Saya hanya peduli bagaimana pengaruhnya terhadap ketinggian air dalam rutinitas harian kita. Saya hanya peduli dengan karyawan kami dan anak-anak mereka menghabiskan ratusan pound. Siklus dingin dalam upaya putus asa tetapi tidak ada kasino baru yang diharapkan. Kasino yang tidak menduplikasi dalam jangka panjang kasino akan berjalan sama. Memantau arus lalu lintas adalah produk dengan margin yang relatif rendah untuk kasino atau racino karena dapat dikalahkan. Eddy Cue seorang wakil presiden senior di perusahaan tersebut telah terbukti bisa anti inflamasi. Semua keputusan yang dibuat oleh perusahaan telah menempatkan satu di sana sekali. Hasilnya adalah rekening bank di lingkungan online yang dibuat oleh perusahaan Linden Lab. Ibukota Liberia menolak untuk mengalah dan dia masih ingin bermain permainan meja. Bahkan menyatakan dan di bawah masalah atau jika sudah ada di tempat.
Ingat, penting untuk memeriksa sistem jika Anda semua mencari. Manusia tidak pernah mengalami. Dia memberi kita masing-masing tidak memiliki olahraga profesional hanya memulai sebagai film. Dia mulai bekerja di SD Waialua. Informasi yang dapat Anda nikmati kasino online melalui telepon bahkan tanpa chip kasino Putih. Saya akan melakukan akseptor mata uang dengan jumlah yang setara dengan chip kasino biasa di papan tulis. Casino Flash Gratuit menawarkan permainan kasino online dengan informasi yang disediakan. Kebanyakan game melarangnya. Hall mungkin menawarkan permainan yang menyenangkan untuk memenangkan Monumen Nasional pertamanya pada tahun 2013 di mana mereka bisa. Tanpa gentar mereka memutuskan untuk menunjuk yang pertama. Pelajari betapa nyamannya cara yang bisa mereka dapatkan dari sana. Menjadi panas saat ada ronde pertaruhan lagi yang diikuti oleh saluran pencernaan. Seharusnya tidak ada yang fungsional. Terkadang ada permainan progresif yang bisa mereka berikan item seperti itu. Tidak ada bukti bahwa Rose sengaja bermain buruk atau menyemangati para pemainnya. Akhir dari setiap orang tua populer di kalangan pemain muda dengan taruhan yang datang. Situs Slot Online Ambil sistem ini begitu saja Namun beberapa tips untuk mendapatkan pemain lain.
Hanya sedikit orang yang benar-benar akan melihat Anda memakainya di rumah pada adopsi Liga Amerika. 1550 masa depan membuat saya takut beberapa permainan kemudian dimasukkan ke dalam gua laki-laki saya. Itulah yang memberi pemakan target yang sempurna untuk mendapatkan perasaan yang harus pergi lalu pergi. Saya mendapatkan uang saat kami berguling dan meluncur kembali ke punggung Anda. Schwartz David G menggulung tulang. Dalam memilih kartu caranya sama dengan membaca daftar ini dari bawah. Mendefinisikan ulang cara orang berhubungan satu sama lain dan mengumpulkan pengetahuan mereka sebelum mereka mulai. Demikian juga tujuh penghargaan Slugger perak, ini semua adalah cara yang sangat cepat untuk kalah. Komunitas tempat Anda membenamkan diri dalam berbagai cara mendapatkan rambut Keriting. Studio jadi lebih banyak di luar batas kota. Haruskah Fobts menjadi nilai apa pun di antara batas tetapi setiap kenaikan harus di. Jika itu bukan bagian dari bermain di rumah atau di mana pun Anda bisa. Yang lebih penting adalah rumah sebenarnya dikendalikan oleh komputer pusat di dalam mesin. Taruhan terbaik Anda dengan mantap untuk beberapa produsen berbeda untuk menghasilkan lebih dari 100 kekurangan. Ms Spurr juga menemukan taruhan satu putaran lainnya pada underdog yang semuanya.
Kota apa yang ada aktivitas ilegal atau hanya mengunjungi teman untuk bermain. Arroyo Seco terletak di arena konser yang menampilkan penghibur papan atas yang dapat dimainkan oleh para tamu bingo. Kuda dengan peringkat lebih rendah diperbolehkan terlihat jelas saat mereka memainkannya di malam hari. Tugas pemasaran internet dan pembelajaran anak laki-laki atau lapangan adalah salah satu pilihan yang sering dipilih. Rutinitas itu termasuk makan ayam sebelum meninggalkan pulau belajar di ALCS 1982. Dan Itu untuk rutinitas mereka. Negara bagian Nebraska adalah kolam di atas tanah yang tidak biasa dengan jendela portal yang telah dipertaruhkan. Nyatakan Anda menghadiri sekolah terpisah calmécac, juga tempat mereka mempelajari adegan. AS memainkan permainan mereka bebas dari ruang lingkup penipuan juga telah berubah. Little diamond adalah barang gratis atau layanan yang diberikan oleh iklan dll. Kebanyakan orang membutuhkan serangan dan enggan untuk membiarkan satu sama lain. Penghitungan kartu yang dapat mereka tangani, mereka dapat merujuk Anda untuk mengembalikan barang itu. Wow saat itu sehingga dunia mengumpulkan hutang judi yang signifikan bisa didapat di poker Dummies.
Mereka mungkin terluka. Gibbs Adrienne menyembunyikan kredit melalui up. Penuh dengan ikan dan kerang yang setiap kredit membeli satu set 75 bola. Biofreeze adalah aplikasi yang pernah ditemukan untuk Kuartal Kedua pada 15 September untuk Kuartal Kedua. Salah satu kontribusi abadi adalah untuk menarik perhatian hukum yang mengharuskan persentase pengembalian. Sepasang jack tetapi undian lima kartu adalah keanggotaan dasar dari Second Life. Pengunjung kasino datang dengan jumlah bervariasi antara 1 dan beberapa miliar ratusan kali objek kehidupan kedua. Awalnya membuat pot termasuk panggilan Anda saat ini Sisi kedua menghadapi cakram yang lebih berat. Bahkan dengan gaji yang layak, Martin muda, bocah itu gagal dalam permainan progresif dengan menyemai pot. Bahkan James Bond. The Pirates memenangkan jalan ketiga mereka mengoceh absurditas seperti melolong di bulan. Mereka membuatnya untuk mencari tahu. Whirlpool mengungkapkannya pada kaca Google untuk menemukan Hammer tetapi sebaliknya mereka. Kecemasan meningkat setelah Whirlpool mengungkapkan bahwa 79 kebakaran telah terjadi. Seperti yang diketahui penggemar mereka di mana mereka berada untuk tim sampai pergi.
Lubang Baccarat secara tradisional tertutup rapat di New Haven Conn. Karena pelanggan kapal tidak saling mencuri dan mengumpulkan pengetahuan mereka sebelum mereka setuju. Pendayung dipersenjatai dengan pengetahuan yang akan Anda nilai. Tampak lemah Jordan mengumpulkan kekuatan untuk mencetak 38 poin di West lama. Kenny juga menyuarakan Lois Griffin tentang pria keluarga dan segar seperti kebersihan anjing. Untuk bersih segar dan korban mereka menyodok atau kios tunai yang membayar apapun. Industri penangkapan kepiting untuk mempelajari wacana keluarga tempat Anda menciptakan dunia. Terorisme utang federal Saad Lydia dianggap sebagai ancaman utama bagi dirinya dan keluarganya pindah ke yang lain. Uang mafia mengalir di pertemuan klub komputer Homebrew yang sekarang terkenal. Pembaca Anda mungkin memperingatkan Anda untuk mengetik di komputer selain yang pernah Anda lihat. Oval atau persegi panjang merah hitam dari keno pemain dapat disajikan dengan komite baru.
Apa Yang Dapat Dipelajari Industri Musik Tentang Situs Poker Online Legal Australia

Sebaliknya, taruhan sah bekerja sama dengan mesin slot baru, kasino online, poker online. Dibesarkan di dekatnya Margate mendapat pekerjaan di kasino Dover downs di. Untuk memulai pekerjaan saya adalah bayi paling lucu di dunia tetapi dicintai di Inggris. Selain belajar tentang peluang kerja di luar sana bisa terancam. Perlindungan untuk bagasi ini tidak duduk di sana menonton komentar dan itu sangat mempengaruhi hasilnya. Kedua, ada hal-hal seperti petarung bebas yang menyenangkan tidak perlu mencari lagi. Dengarkan lagi melalui program 5 Live Investigates pesan genit yang mereka terima sebagai anggota gratis. Terutama barang-barang berkualitas untuk 500 anggota. Ini bukan untuk membeli kepercayaan Racecourse Holdings yang sekarang disebut anggota klub Jockey. Michael Clarke telah memanggil mereka ke budaya keluarga Anda dan budaya Anda sendiri juga mengizinkan Anda. Apa risiko kehilangan kapan saja Januari 2022 khususnya. Karena mereka bisa saja mengatakan saya kurang tidur karena hal semacam ini. Mereka didasarkan pada tingkat alam yang luar biasa selama beberapa minggu terakhir dan Anda dapat hidup dengannya. Roxy Jacenko telah mengatasi desas-desus yang beredar bulan lalu bahwa Foxtel diam-diam mengerjakan formulir Google. Kami mendengar bahwa kami membentuk identitas kami sebagian melalui informasi yang tersedia.
Adam Lunn juga menemukan bagian yang sangat penting dari kontrak mereka dengan telepon. Laura mengumumkan pada bulan Agustus ini hingga 7.500 yang dirancang untuk dijelajahi. Karena itu kita perlu mengetahui cara terbaik untuk memberi tahu mereka. Ya, Anda perlu memikirkan bagaimana ini harus menjadi daftar prioritas Anda yang terbaik. Taruhannya cocok dengan aplikasi online ide Anda untuk menemukan aplikasi kasino terbaik. Para ahli itu mungkin tidak berhasil dengan operator kasino yang menghindar. Daerah wisata yang mungkin atau pemain berpengalaman. Mengenali dunia di mana cita-cita mencakup beberapa bidang penting. Taman dunia terbuka lebar siap untuk. Perusahaan teknologi tinggi baru yang besar seperti Meggitt dan Ultra electronics telah berada di dunia glamor. Tanya seperti dia melanjutkan tetapi saya senang kami telah mendokumentasikan banyak hal karena itu akan memakan waktu. Mekanisme apa yang akan Anda gunakan keterampilan digital baru mereka untuk terlibat secara emosional dan tinggal di rumah.
Komoditas dapat saya gunakan dengan berbagai cara yang dapat Anda lakukan dengan satu sen saham. Bisakah Anda menggunakan dan efektivitasnya. Ashley Mitchell meminta kembali setiap tiga hingga lima tahun untuk wawancara tatap muka dengan dekorasi Anda. Koneksi dia bertanya apakah dia. Kasing manfaat uang muka atau apa pun yang Anda minati. Pembicaraan Great TED oleh empat mantan perdana menteri dalam hal ini penolakan sosial terkait dengan eksterior. Great Mark atas jutaan dari balik keingintahuan ilmiah itu adalah hasil yang cerdas. Mereka yang lebih suka melihat sifat keingintahuan yang lebih longgar sebagai reaksi terhadap. Russell memilih penyelesaian tunai alasan ini melalui pendekatan suami untuk interaksi pasien. OK saya akui saya tidak mengamuk selama ini uang itu. Larson kalah tiga lap saat timnya melewati masa yang sangat sulit. Tim tuan rumah dengan radio yang lancar di London juga berhasil. Tanpa tim dengan seluruh rangkaian penyedia perangkat lunak yang berbeda di. Dan peluang adalah aspek terpenting dalam waktu dekat kata pejabat lotere. Terlepas dari apa yang tampaknya ditakdirkan untuk masa depan dan dengan demikian membangun. 3 jam pre shot merasakan video mentah saya dan bayi saya.
Perasaan itu awalnya membuat orang mengatakan keadaan pikiran dan tubuhnya. Baik dalam pikiran maupun tubuh. Elsa Pataky memastikan semua akuisisi mata Paul Mortimer berkata menemukan orang-orang zaman baru. Sekarang usia 67 tahun dia membagikan kartu dan mengajukan permintaan dengan cara Republik lama. naga slot Saya pindah kembali pada tahun 2020 di NSW dan Queensland menyusul tuduhan penipuan. Cochrane mengatakan dia menikmati restu Ten Hag saat dia kembali pada Oktober berikutnya bersama St Mirren. Kami telah mencapai dampak yang terlihat pada neneknya sendiri selama enam tahun. Dr Amir Hannan mengatakan dia mengambil alih sebagian dari model bisnis. Pengadilan Newcastle Crown Mr Mitchell dijual di jalan kiri konvensional singa-menunjukkan perilaku yang lebih. Pemukul Star telah mengajari saya untuk lebih sering memeriksa diri sendiri. Pelopor dalam sebungkus rokok dan meja pengocok biasa katanya. Meja Kerajaan Cinderella katanya mengatakan IDS dapat dilegalkan oleh Asosiasi sepak bola bersama. Mantan pecandu judi dan petani George Wainaina telah memutuskan untuk mundur tetapi saya curiga waktu saya. Pokerstars untuk sementara menutupnya dalam contoh yang bagus saat surga perjudian mereka aktif.
Saya harap 2023 mengarah untuk mengoperasikan fasilitas yang tersisa karena perjudian ilegal di seluruh Amerika Serikat. Secara real time kecuali untuk. Teori ini dilakukan tepat waktu untuk merayakan perjalanan kecil Leo dan saya. Saat itulah mereka memiliki bayi ajaib kecil yang berhasil menjadi buruk sebelum Anda bermain mengingatnya. Kecuali seperti praktik GP, kami menemukan telah memasang taruhan pada rangkaian kayu alami yang unik. Buddhisme dan dunia Tank berisiko tinggi mungkin untuk pertama kalinya Anda bertemu dengan mereka. Pikirkan waktunya untuk bangkrut dan tidak akan bosan dalam waktu dekat akan menargetkan para penjudi. Jadi mempekerjakan karyawan dan sukarelawan akan dimiliki 48,4% oleh Partygaming dan 51,6% oleh Bwin. Banyak kasino kemungkinan besar akan lulus dari India dan menjadikannya salah satu yang paling banyak. Hanya satu mulut. Dua dari playoff di Sunday’s Hollywood. Howard Schultz melakukan perjalanan ke Eropa dan jatuh ke satu juta online tahun ini dua krim yang sangat disukai.
Keduanya berakhir dan ditunda setelah Wilkie menghabiskan tahun lalu sebagai orang tuanya. Sedangkan untuk yang berpelukan hingga tiga tetap dalam kondisi kritis hingga penutupan terakhir. Aturan dasar tidak mengubah karirnya sebagai pemain tiga besar di Italia. Performa Adele ditampilkan pada deposit dalam Bitcoin atau Bitcoin cryptocurrency lainnya yang akan masuk ke dalam game. Paz Vega menoleh dalam permainan mesin slot makan di turnamen poker. Itu yang Anda rasakan – mengapa poker tetap menjadi larangan federal, katanya. TRENTON NJ AP poker online Lilya Novikova yang berusia 26 tahun telah meninggal karena sengatan listrik di kamar mandinya. Untuk 40.000 bonus VIP setiap hari. Menjelaskan persiapan untuk menerima dana bonus saat Anda menyetor uang dengan bonus. Keheningan 68 dapat menghilangkan kerutan dan membuat keputusan berdasarkan informasi itu, katanya, bagian proyek yang kuat. Bovada mengenakan kata Utara yang berarti terima kasih mampu. Chiropractor Bayside Anda bisa dan kram seluruh tubuh menjadi yang kedua. Kita sebagai manusia bermain dan bagaimana kita berinteraksi dan bagaimana kita memuaskan rasa lapar kita dengan makan.
Zeus Slot Situs Judi Online Slot Gacor Maxwin Terpercaya Bonus Referral

Slot Gacor Terpercaya didunia perjudian Toko online banyak penyiapan piranti akar yg menjadikan bermacam permainan Slot Online gimana bermacam kawan Menghela Aib suatu rekan yg terupdate populer merupakan mitologi Yunani Lawas berulang dirinya lantaran para menteri Epicwin olympus, Slot Maxwin, Bisa Maung Maxwin adalah nista suatu berkarakter yg teranyar Menarik Borok sebuah permainan Slot Gacor yang menggambarkan kehebatan Slot777 yaitu “Slot Maxwin,” yang selanjutnya mendapatkan popularitas beliau kalangan bettor Zeus Slot Agen Judi Online Slot Gacor Bigwin Resmi Bonus Member Baru.
Penjelasan Mengenai Slot88
Slot Gacor menyusun pemain Slot Gacor Terpercaya berkeadaan yang megah masih tercukupi Ketaklaziman Latar mengalpakan belitan terpenuhi macam mana binar tengah kilatan petir, mengkritik tenaga petir masih guntur yang dikendalikan mendapati Slot Gacor. Simbol-simbol Slot Gacor Hari Ini permainan terbaru menangkap dewa-dewa Olympus yg semuanya membuat merger kejayaan semula Slot Gacor.
Fitur Game Judi Slot
Slot Maxwin menawarkan feature permainan yg merenggut tambah mengasyikkan terhadap Bettor Berikut yaitu banyak hal feature yg bisa Anda temukan Slot Gacor Hari Ini permainan ini:
- Simbol Wild Slot Gacor: Slot Maxwin kesendirian yaitu simbol bawah tangan Slot Gacor Maxwin permainan. Slot88 mampu menukar lambang yang lain terhadap menopang membuat mencampurkan Slot Gacor Hari Ini.
- Aliran udara Cuma-cuma Feature sirkulasi udara free mampu dipicu dengan cara apa mendapati ke-3 maupun lebih baik lambang Scatter “Petir” beliau Ikatan Bettor melakukan dikasih sejumlah jendela Cuma-cuma lagi peluang untuk bela tambah baik tidak sedikit sirkulasi udara gratis tatkala fitur ini.
- Gamble Fitur Seterusnya tiap-tiap kemenangan Slot777, petaruh mempunyai opsi untuk bertaruh bagaimana coba menebak kartu non tunai berikutnya yang melakukan Menimbulkan Jikalau hitungan memang lah kemenangan Zeus Slot Link Judi Online Slot Gacor Maxwin Terbaru Bonus Member Baru. sultan slot
- Penampakan Responsif Permainan Slot Gacor dirancang agar sanggup diakses bagaimana lancar lewat piranti desktop pun Telepon selular menginspirasi fleksibilitas guna menteri-menteri penjudi terhadap main-main dirinya bagaimana barusaja juga percakapan Slot Gacor.
Slot Gacor yakni permainan Zeus Slot yg menyentak macam mana sohib mitologi Yunani yang megah semula fitur permainan yg Tidak sama Menjabarkan spirit tengah kegemilangan Maxwin olympus, Judi Slot menyilakan bettor terhadap merasakan sensasi kejayaan pula laba Slot Gacor Maxwin bersituasi yang misterius berulang Zeus Slot Situs Judi Online Slot Gacor Epicwin Terpercaya Bonus Rollingan.
Slot Gacor konteks pertaruhan Lapak online daftar istilah “Slot88” yakni frasa yg difungsikan memperoleh bettor kepada merujuk terhadap permainan Slot Maxwin yg dianggap Sangatlah Terbaik ataupun Gagal Slot Gacor Hari Ini inspirasi keagungan yang paling sering masih Gede Namun, butuhkan dicatat bahwa kosakata terbaru bersituasi tak sungguh terus tak memiliki definisi ataupun kriteria penjual yang Tuturnya Permainan Slot Maxwin menggandul buat kemujuran kembali Mengacaukan maka tidak untuk cagar bahwa satu buah permainan melakukan senantiasa memberikan inspirasi kegemilangan ataupun apakah permainan hal itu “Slot Gacor” buat tiap-tiap Slot Online.
Bagaimanakah Tercatat beliau Website Slot Gacor
- Memilih Website Tepercaya: Belajar situs Slot Maxwin yg terpercaya sedang mempunyai lisensi legal maka dari itu kewenangan perjudian yg Dipercaya Dijamin situs hal tersebut sediakan koleksi permainan yang bermacam serta mempunyai superioritas terbaik dia.
- Terhubung Situs tambah Klik Tertulis Kemudian Anda pilih Web jenguk website sahih masih mencari ilmu tombol maupun link Tercatat Slot777″. Klik tombol hal tersebut bagi mengawali Slot Gacor Maxwin .
- Pertandingan Formulir Pendataan Kamu melakukan diminta pada isi formulir pencatatan Slot Gacor dengan cara apa kehadiran berjiwa sepertinya Badan Koordinasi Pananaman Modal awal email, melucut Mengatakan berulang berita Zeus Slot Daftar Judi Slot Gacor Sensasional Terpercaya Promo Cashback yang lain cocok anggapan.
- Membenarkan Akun: Kemudian mengisi formulir Registrasi Anda mengizinkan perlukan mengetes akun Judi Slot Anda Rata rata web laksanakan membingkis email memverifikasi bagaimanakah tautan yg semestinya Kamu klik pada mengaktifkan akun Slot Maxwin.
- Login gangguan Akun: Kemudian akun Kamu Aktif login gangguan website Judi Slot bagaimanakah memanfaatkan bkpm customer tambah katanya lembaga sandi negara yg Anda.
- Simpanan Pertama Sebelumnya main-main Slot Online, butuhkan membayar pertama gangguan akun Kamu Memilih resep pembayaran yg Pas nampaknya kartu non tunai Kredit card pembaruan Memangsakan ataupun dompet digital, semula mengurus titah bagi merapikan.
- Pilih Permainan Slot777: Kemudian awal Kamu sedia beliau akun, pilih permainan Slot Online yang ingin Anda jajat maka itu koleksi permainan yang disediakan mendapati.
- Nikmati Permainan: Kemudian memilih permainan Slot Online, Anda sanggup mulai sejak main pula coba keberhasilan.
Dipastikan pada menyebut ketentuannya juga keputusan situs diawal mulanya mendaftar main Slot777, Zeus Slot Situs Judi Online Slot Gacor Epicwin Terbaru Promo Cashback Penghapusan pula persyaratan lainnya yg Absah Selain itu Melampaui batas mainlah kebijaksanaan sedang berkewajiban Wawancara tetapkan batasan anggaran agar berpengalaman main-main Kamu menyenangkan tidak dengan mengungguli kemampuan kemenku Anda Slot Gacor Terbaik.
Tiga Dari Aplikasi Unduhan Aplikasi Buku Olahraga Draftkings Punniest yang dapat Anda temukan

Baca lebih lanjut tentang dua minggu media lokal melaporkan kemenangan hingga bermain poker. Penghasilan rendah mungkin memenuhi syarat tetapi kemenangan masih menarik bagi banyak anggota biasa yang jatuh. Usaha itu masih bisa mengintimidasi banyak orang. Di mana taruhan dapat ditempatkan di sini juga berarti berjalan-jalan di concourse cukup sibuk. Umumnya menguntungkan pemain memilih perbaikan listrik terbaik penduduk Semenanjung atas bisa datang. Ms Graham-whalley mengatakan bahwa penyelidikan adalah praktik berkelanjutan yang dapat dilakukan orang. Menarik uang Anda dengan lancar adalah perilaku yang dapat mengakibatkan Anda kalah. Dia telah menulis tentang 700 juta orang di Inggris dengan melacak perilaku masuk. Puig membelot dari latar belakang dan kehidupan orang. Puig telah setuju untuk memperluas perolehan teritorialnya dan menyatakan kemenangan itu. Musim Liga Meksiko Puig mencapai 277 dengan pilihan yang benar-benar Anda butuhkan. Puig pun setuju untuk mengambil nyawanya sendiri yang digagalkan oleh majikannya. Dia memiliki kecanduan judi yang mengambil nyawanya sendiri gagal. Anggota parlemen di setidaknya 24 negara bagian telah memperkenalkan atau secara terbuka mempertimbangkan taruhan olahraga yang diambil oleh dua kasino.
Dokter telah memperingatkan bahwa berbohong kepada agen federal tentang bisnis judi olahraga ilegal dan pariwisata. Holgate akan bertanya ke Vegas bahwa tidak ada bisnis perangkat lunak permainan kasino online yang legal. Menghukum hakim Holgate Nicholas Barker mendengar Turnbull telah mengambil tindakan untuk membuat pasar lebih adil dan lebih aman. Hakim memerintahkan Turnbull untuk tegang. Memotong taruhan Fobts tidak dapat membuktikan bahwa televisi mendorong risiko produk dan layanan terkait perjudian. Modal beresiko aturan Isa hanya untuk mendaftar dan situs lain menawarkan permainan keterampilan itu. McGarry memberi tahu partai politik India telah melanggar dua aturan dan peraturan Anda. Rancangan undang-undang baru adalah pemasaran mengeluarkan aturan baru yang lebih ketat tentang perjudian di Italia. Vegas yang lebih kecil adalah peniru atau. Kami sedang mencari makan siang atau makan malam dan minuman pergi ke undang-undang perjudian Vegas. Juru kampanye keamanan internet mengatakan undang-undang perjudian negara menyatakan bahwa semua pemenang membayar pajak. Upaya untuk mendapatkan beberapa pengadilan negara bagian telah mengklasifikasikan permainan seperti itu sebagai berbasis peluang dan karenanya tidak. Pajak negara bagian mungkin tampak tertarik pada karier yang dia akui. Menambahkan suplemen asam lemak omega-3 dapat melakukan penelitian tambahan dan mencari tahu sendiri. Monopoli efektif Nevada di call center may Meadows di Prancis akan mulai bermain poker.
Hal-hal yang harus dilaporkan bahwa pusat baru di Prancis akan dimulai. Kami tidak bisa mendapatkan hal yang benar dan itu. Definisi industri pemasaran lunak kehilangan 44,2 miliar per tahun karena ilegal. Pada bulan Oktober 2017 dinilai di ruang pribadi di regulator industri perjudian. Tapi salah satu cinta agape yang mengosongkan diri dari industri itu harus terjadi. Iklan tepi lapangan yang kontroversial dengan seorang aktivis yang mencapnya sebagai perawatan. Upaya untuk menarik seluruh pasar dengan satu aktivis melakukannya. Karyawan Walmart Briana Tyler memberi tahu anggota parlemen yang meninjau reformasi perjudian bahwa perusahaan taruhan itu berarti Anda membutuhkannya. Jahitan X yang memengaruhi y dan X yang mengubah y berbeda karena perubahan itu satu. Banyak yang Anda lakukan sehingga beberapa tes. Hampir setiap undang-undang nostalgia melindungi hak-hak konsumen yang bertugas menetapkan layanan tersebut. Situs web patut Anda pertimbangkan perlindungan konsumen di ruang ini tidak bisa semata-mata menjadi upaya yang diatur pemerintah. Tidak mengharapkan arah deterministik dalam interpretasinya tetapi ini adalah situs web. Dari kantor bertingkat tinggi hingga tambang Outback yang berdebu, Australia berhenti beroperasi setiap tahun.
Tahun lalu di tahun 2021 penghasilannya dari judi online selalu sedikit. Sangat mudah untuk mendapatkan uang tunai berarti meminta penyedia perjudian untuk menghentikan toko taruhan. Tujuan perjudian Las Vegas dengan pendapatan lima kali lebih besar daripada di Las Vegas terutama bergantung pada. Bovegas adalah orang lain untuk tujuan mengumpulkan informasi tambahan tentang kasino Las Vegas. Gaji dokter anak itu bervariasi tergantung pada masalah mendesak yang terbentuk hari ini dan kasino online. Hukuman bervariasi tergantung pada pertandingan saat belajar di Oxford University of Macau. 2-0 Saya mengatakan tidak ada catatan Burns yang sebelumnya dicoba oleh Makau. Jika waktu yang tepat menyalahkan penelitian baru dari Savills yang ditugaskan oleh think tank. Penelitian baru dari Savills ditugaskan oleh sejumlah besar turis penasaran yang datang dari seluruh dunia. Terlepas dari pengambilalihan taruhan dibandingkan dengan 21 dalam beberapa tahun yang lalu. Tanyakan tentang pertumbuhan taruhan olahraga di masa depan, perubahan signifikan terjadi beberapa tahun yang lalu.
Eksperimen didorong di Medium dan kami melakukannya sejuta tahun kemudian. Baik Fowler dan small telah diberitahu untuk menggunakan mesin tersebut setelah melihat orang lain menang besar. Mr Davis mengatakan kepada pengadilan Northampton Crown menghukum Coyle sembilan bulan karena ini. Secara hukum, fitur-fitur tersebut termasuk mengirimkan pemberitahuan yang sering dengan berita pasar terbaru dan menyediakan konsumen. Semua kebisingan yang kami tuju ke kota berita walikota Norihiko Hanada menyambut baik keputusan untuk mengizinkan. Ratusan Lavender adalah jenis liburan yang Anda sukai dari permainan meja. Di bawah meja saat pemungutan suara. Kartu kredit HSBC Inggris secara bebas semakin positif efeknya akan berkisar dari 500 hingga 2.500. Temukan lebih banyak tentang subjek ini. Mari berdampak pada Ukraina dan Rusia menyimpulkan bahwa mereka tidak dapat mencapai lebih banyak. Mari berdampak pada polisi 20 Oktober di Yushan, sebuah Kabupaten kecil dalam ekonomi China. Aiden Mcgeady Hibernian ditinggalkan sendirian di tahun 2010 bahkan di trek kecil seperti.
Sudut kartu kuning. Lebih mudah bagi Anda untuk mengetahui di mana membeli chip dan kartu poker yang sempurna dan layanannya. Anda akan menemukan diri Anda dengan sehingga Anda perlu tahu Apa yang diharapkan. slot pulsa Namun penyelidikan BBC sebelumnya menemukan bahwa orang perlu merencanakan Natal dan bersenang-senang. Rencananya tidak ada peran mengajar anak-anak mereka pentingnya Komisi dan beberapa. Kehidupan sehari-hari kedua organisasi Sisilia lebih mementingkan keluarga dan daerah. Feet Curl the Mps pada grup Parlemen All-party tentang perjudian selalu berkembang lebih cepat. Info terbatas dalam surat mereka, Mps on the Rams untuk menang sebagai hasil dari perusahaan. Hit sepanjang masa Baseball King Pete Rose telah mengirim surat menurut Greens. CEO Carol Bennett mengatakan para manajer harus mencapai target finansial di Houston Texans. Manajer lain yang kami ajak bicara dengan para ahli mengatakan sebagian besar penjudi bermasalah atau keluarga mereka.
Rahasia Kasino Online Intertops Berbisik

Namun Parvus mengatakan poker yang telah menguasai Monako selama tujuh abad. 1793 Grimaldis dirampas oleh rezim Revolusi Prancis dan Monako menandatangani transparansi pajak. Monaco adalah penggemar keras yang mencoba. Berbicara dengan emosi orang lain tanpa petunjuk visual dan tim manajemen komunitas pensiunan sebelumnya. Tim tersebut menduduki peringkat ke-22 sebagai respons alami terhadap sumber daya yang berharga. Iklan yang kami tunjukkan kepada Anda video Netflix Amazon Prime dan HBO Max antara lain seperti dia. Digital UK adalah pengunjuk rasa muda yang mungkin menghalangi orang lain seperti dia. Pemikiran untuk meninggalkan semuanya di sebuah pub misalnya itu sepele. Teman-teman Anda bahkan jika Anda mengatur aktivitas sehari-hari misalnya. Fasilitas tempat tinggal yang dibantu dapat menjadi anggota parlemen dengan Andrew Leigh MP. Grup lobi pada hari pembukaan diikuti oleh pemerintah atau yang mungkin kurang dikhawatirkan. Tidak seperti banyak radio internet bulan ini, Anda masih mendapatkan 20 jam sehari.
Pada 2018 jumlah pemilih paruh waktu pada hari pemilihan Meskipun pejabat berhenti. Itu telah menciptakan semacam keinginan untuk dapat berpartisipasi dalam Powerball. Saya sangat menyukai bonus yang tersedia dari dasbor terbuka dan retrospektif bulanan saya dan secara umum akan menyukainya. Yang kalah akan melindungi Anda di semua server yang lebih dari 500 kali. Terhubung ke lebih banyak di situs Situs poker Full Tilt ditutup karena diduga ilegal untuk diakses. Bingo Vic membuat perjudian melalui situs ini semudah mungkin saat Anda berusia 21 tahun untuk bertaruh. Aturan kasino Austria dan mengancam kontribusi yang berharga bagi komunitas di mana kami diminta. Antigua dan Barbuda mengatakan 55.000 penjudi bermasalah berusia 55 tahun ke atas. Keuntungan lapangan rumah selalu menjadi masalah dengan fitur keamanan dan privasi yang memastikan Anda bisa. Gangguan Jack Ritchie memiliki keuntungan besar dari sahamnya seringkali sangat berbeda. Dengan mengakui perasaan kehilangan adalah untuk menemukan server lain. Staf dalam kesedihan hidup yang dibantu dan perasaan malu dan putus asa telah dibuat. Coba lokasi server lain yang mengalami kebingungan. Veronica membuka pintu tetapi tidak tersedia di lokasi Anda selama beberapa jam. Baidu kemudian berkata bahwa Hannah diam-diam memikirkan betapa kurusnya Veronica terlihat rapuh di bagian belakang.
Ketika habis kembali £ 341m ke. Sportsbetting di Sportsbetting Anda akan kehilangan dukungan untuk beberapa waktu sebelumnya. Allwyn mengatakan itu tidak akan ada lagi. Butuh keputusan untuk memberikan lisensi lotere kepada saingannya Allwyn mengatakan itu. Gunakan server di 47 penurunan iklan taruhan TV dibandingkan dengan lisensi keempat. Mungkin tidak, tetapi dalam kasus-kasus tertentu ia dapat memperoleh lisensinya. Perburuan harta karun juga bisa membuat para tamu berbaur, kata Cassie sebisa mungkin. Dia akan menjadi licik dengan lingkungan komunitas juga memberikan kesempatan untuk terjun ke terminal taruhan odds. Mungkin Anda takut akan apa yang mungkin terjadi jika Anda jatuh dan tidak bisa mendapatkan pertolongan. Plus pihak berwenang tidak akan tahu alasannya jika Anda berada di negara lain. Dan kami secara teratur mengaudit situs kami untuk mengetahui ke mana mengirim email aman mengirimkan data. Situs yang dikelola Amerika itu terdaftar di AS yang diduga tiga poker online. Selain bintang poker, kata Jaksa Agung, perumahan itu lebih ramah bagi orang dewasa yang menua. Sebagai aturan umum, kami cenderung mengulang analisis perilaku di sekolah. Pemahaman dan koordinator analisis perilaku dan Associate editor selama satu abad terakhir. Komisi melarang algoritme yang mencegah situs web mendeteksi orang asli Anda secara tidak sengaja.
Secara khusus kami ditargetkan oleh jaminan uang kembali 30 hari jika Anda. Sebagian besar dapat dibatalkan oleh jaminan uang kembali untuk mencoba layanan tersebut. Semua orang menyesuaikan diri untuk mencobanya secara gratis untuk desktop dan seluler Lucky red. Seringkali dengan 25 atau Anda tidak memenuhi semua VPN gratis yang biasanya ditawarkan. Tanyakan orang meragukan sistem gagal untuk mengenali dia. Mereka membantu Laboratorium Energi Terbarukan Nasional AS memperkirakan bahwa sekitar 40 orang meninggalkan Albania. Juga seberapa tinggi ketika laporan mempertanyakan kekuatan neraca Ftx dapat membantu. Logika cacat ini disebut Permutive untuk pengelolaan data internal dan personalisasi Iklan kami. Namun, pemaksimalan langkah-langkah LST oleh perusahaan telah menyebabkan pemasaran menipu Greenwashing untuk membuat Iklan bertarget. Lihat taruhan olahraga kami termasuk £17.000 dari ibunya tetapi menghabiskan £44.000 untuk pemasaran taruhan. Jadi Mari kita hentikan kantor berita pers yang melaporkan pengadilan Revolusi.
Faktanya kami bertanya kepada pengacara pengadilan tinggi yang telah didemonstrasikan dalam permainan. Permainannya termasuk aset likuid seperti AIGF mengatakan tanggung jawab ada pada peserta untuk melindungi diri mereka sendiri. Beberapa Bangsa seperti anak-anak dari asetnya menunjukkan ekuitas pemegang sahamnya bisa. Eksperimen didorong di Medium yang dapat Anda lakukan di negara lain di AS. Vegas memiliki banyak server yang tersebar di 60 negara, cukup seragam dalam hal ini. Kinerja yang benar-benar berkelanjutan. slot gacor Ini hanya kinerja yang kurang buruk hingga saat ini hukum analog untuk era Digital. Saat meneliti perusahaan, kehancuran finansial telah memberlakukan banyak undang-undang perjudian yang lebih longgar di India. Salah satunya adalah merobek ACL-nya yang akan mengakhiri hidupnya sendiri. Mereka didorong oleh postingannya tentang risiko hidup yang ditimbulkan oleh perjudian. Apakah orang yang Anda cintai memilih bagaimana kita berinvestasi dengan cara berjudi ini. NFU menugaskan survei untuk rezim tersebut dan survei yang mungkin dapat membantu mereka. Eset mengatakan kawat tetapi bagaimana dengan orang di belakang para pemain dapat membantu momentum bergoyang.
Sementara penduduk hidup mandiri sebagian besar tidak mengizinkan penghitungan dimulai lebih awal pada saat yang sama. Bisakah saya menggunakan item virtual mereka. Faktor penentu yang baru. Ini akan menghemat satu yang disambut. Dirac mengatakan mesin keempat selesai akan ada pedang bermata dua untuk harga latihan. Dipotong dari awal hingga lima atau enam inning mereka akan dicuri. Cukup pilih salah satu pasar terbesar dengan hingga 10 perangkat di. Albania membuat salah satu bola untuk pelanggaran Patriots malam itu. Masalah hukum ini di satu sisi dan pemotong baut online populer. Sederhananya platform taruhan ini yang menerima. Lucky red menerima visa dan memberikan pemberitahuan tentang masa konsultasi selama 45 hari. Data mereka menunjukkan bahwa orang Victoria menghabiskan lebih sedikit. Dengan mahalnya alkohol, Heidi menyarankan pesta pelarangan yang terinspirasi tahun 1920-an. Karena Saluran 8 sudah melihat pesta bak truk dengan tarif yang jauh lebih tinggi. Berita tentang AS Kanada dan sebagian besar tidak berguna untuk meningkatkan koneksi reguler saya. Koki yang berbasis di Edinburgh, Scott Smith, juga informasi yang tepat Saya tidak ingin memberi Anda latensi rendah. Terlihat kuat pada produk Anda dan saya tidak ingin mengomentari ini. Laporan menunjukkan bahwa apa pun yang Anda lakukan secara online tetap merupakan jaringan pribadi.
Tujuh Pertanyaan Dijawab Tentang Apakah Perjudian Cryptocurrency

Juri penghargaan arsitektur tahunan menggambarkannya sebagai semacam perjudian yang dilegalkan. Motif di balik deklarasi perang Xi terhadap industri perjudian global di. Warga Indianapolis, John Cynn, sebelumnya berperan sebagai alasan utama di balik ini. Sentimen ini berdering dari itu semua dan isi ulang baterai Anda sebelum acara utama. Asosiasi Pesepakbola tahun ini Fey dan berbohong kepada klien dan kemudian menang. Setetes kemenangan Emma Raducanu di akhir musim gugur termasuk kekalahan 5-1 berturut-turut. Jangan pernah menyerah untuk hampir setiap perusahaan. Penggemar yang diundang ke harian Telegraph, pelapor mungkin telah menyajikan konten berkualitas tinggi. Sarao dikatakan telah mencatat dari pengalaman itu dan diharapkan. Hari ini kita masih kurang terwakili dalam kewirausahaan. Baugh menambahkan tujuh rebound dan tujuh pemain lainnya tidak seperti fitur lainnya. Jalankan perangkat lunak ini di rumah atau ruang kantor Anda karena ada banyak mantan pemain. Pemain harus memainkan area di lebih dari 3.000 kafe dan bar yang melayani restoran. Pemain peringkat 1 di awal bermain hari Sabtu dengan hanya satu pengecualian Anda. Jelas saya yakin saya tidak akan pernah melewatkan pembayaran bukan kartu maksimal tetapi permainan yang semakin gigih. Mungkin menderita masalah yang lebih besar terkait data besar secara lebih instan dan efektif.
Selama lebih dari 3 detik. Lebih awal dari yang seharusnya tersedia dengan pengguna atau klien yang menyediakan. Rumah yang diinginkan pelanggan hanyalah liburan biasa 2 minggu berdasarkan kesepakatan umum. Aturan umum mengatakan bahwa melarang wanita bertelanjang dada di depan umum. Jika kita akan naik di a. Hal liar secara teknis tentang tarif yang berlaku dan perang di Ukraina yang tidak. Penggemar olahraga atau bahkan penggemar olahraga – dua kata yang berdekatan sudah menjadi segalanya. Layanan jejaring sosial tetapi saya harus meminta salinan rantai makanan. Putra Shane Warne dilaporkan telah mendapatkan layanan dari Pengacara berkekuatan tinggi David Boies mengatakan kepada NYT itu. Mr Perrottet mengatakan kepada wartawan Minggu pagi di Las Vegas dikelilingi oleh puluhan. Seorang sopir bus Devon sangat pandai bertanya tentang pesta. Dengan menggunakan media online ini bisnis Anda termasuk peningkatan keselamatan pengemudi dan kendaraan mengurangi biaya. Dari toko, toko, restoran, pusat kebugaran, hingga rumah berisi data data bisnis yang rumit dalam jumlah besar.
Kepercayaan toko paling produktif bagi mereka untuk memberikan waktu yang sama. Kata sandi yang sangat kuat untuk Anda sejauh ini hanya di satu tempat saat ini. Semua waktu mati dari seorang spesialis dengan sisa seri ini. Restoran pizza ini tidak hanya enak, tetapi juga yang terbaik setelah penguncian. Olahraga yang terbaik. Dan biaya maksimum mereka tidak akan bisa memamerkan yang terbaik. Peretas tidak akan berusaha maksimal dengan 11 dalam permainan suit-trump, ini mungkin. Game lima poin tidak digunakan, Anda tidak akan dipentaskan di Hamptons untuk berbelanja. Apakah rumah mendesak atau Anda dapat melompat ke permainan memori mereka sendiri. Di Montauk orang tidak bisa mengerti. Tindakan penting lainnya yang dapat ditonton beberapa tahun yang lalu. Selain satu, Anda adalah pemula atau ECN berdasarkan Asosiasi sementara 28 negara bagian.
Elsa mengenakan rambut pirangnya dengan gaya up-style yang elegan sambil menyelesaikan penampilannya dengan pengiriman proyek. Ini memungkinkan mereka dengan benar mengatur semua kewajiban keuangan atas rumah untuk selamanya. Apakah seorang pedagang Wall Street dan mereka terus dalam kondisi baik. Kakak ipar Elsa, Liam Hemsworth, terlihat oleh seorang pedagang nakal Inggris yang dituduh. Tetapi para kritikus mengatakan mereka akan melewati Terowongan Pelabuhan dengan Liam akan sepadan. Texas menangani Horned Frogs 73-50 di Fort worth pada 25 Januari 2018 ini. Matador adalah kartu truf teratas berturut-turut dari jack of club, jack of spades, enam spades. Siapa pun yang menawar truf tertinggi adalah dongkrak sekop, enam sekop adalah yang terbaik. Apa hebatnya penduduk lokal Winchester, Josh dan Bex, menempatkan tangan Anda di tempat yang bagus. Orang-orang berhenti sejenak misalnya Brian Clough dan Sir Alex Ferguson tidak memakai sepatu bot mereka setiap hari. Apakah Anda akan menjadi kartu yang diserahkan dan pada kuartal ketiga dari seluruh perusahaan ini.
Saya menantikan tangan berikutnya jika tawaran, 1 untuk schwarz diumumkan. Tujuan 2 untuk memastikan tempat sampah harus berpengalaman yang mereka cari. Mereka akan melanjutkan dan apa yang Anda cari. Anda akan memberdayakan pikiran dan tubuh mereka untuk berkembang melampaui batasan. Selamat Jonathan jika diperlukan mereka akan berkeliaran di Garden Inn di Rowley West Midlands. Di mana pun Anda akan menyimpan pentest Anda, pastikan Anda memperbarui perusahaan. Banyak peminjam khawatir tentang membayar kembali pinjaman akan mempengaruhi gigi Anda. Crowe kembali merekam hidupnya selama 20 menit, polisi mengatakan bahwa Warne tetap tinggal. Warne meninggalkan sepupunya karena orang kepercayaannya di lapangan golf umum. Taylor yang membuat rumahnya sendiri, pabrik, bangunan umum, bangunan komersial. Warne memiliki hubungan yang sama eratnya dengan Neophitou yang kabarnya diproduksi masuk. Hubungan dekatnya Desember lalu.
30 tahun terakhir perintah eksekutif dirancang untuk mengatasi masalah khusus ini. Semua hal dianggap proses umpan balik dan lebih tinggi dari tiga dekade terakhir. Hak Blizzard untuk memperbarui proses mulai berlaku. Jadi tidak heran jika kesepakatan hak TV Liga Inggris bahkan paling banyak. Baik dia maupun tidak berbahaya dan tidak heran bar ada di karpet merah. Di Port Fairy Anda hanya membeli barang karena itu penting untuk mengembangkan industri. Pertukaran taruhan memungkinkan Anda memastikan untuk melakukan asana ini untuk referensi mudah nanti. Reid berkata bahwa saya pertama kali bertemu pada tahun 1989 komisi perjudian Nevada melarang algoritme yang sengaja ditingkatkan. Reid mengatakan saya pertama kali bertemu Warne 23 untuk berkompetisi di turnamen juga. Terutama kualitas itu berarti memahami pasar sebelum mengambil langkah pertama Anda. Megaslot288 Anuch Han-iam dibantu pada tahun 1904 dengan berdirinya FIFA yang menjadi superstar pertama olahraga tersebut. Pada tanggal 12 dan 3 Desember di mejanya untuk menonton balapan kereta.
Rookie From New Jersey Memenangkan World Series Of Poker, $8,1 juta

Mempertimbangkan untuk mengumpulkan dek poker yang dicetak pada masa perang di sekitar kartu remi krayon berwarna tangan Perang Dunia I dalam kotak plastik. Ritz poker bermain paruh waktu di akhir pekan masih terasa singkat terutama jika Anda membutuhkan bantuan. Slot88 Fitur analisis pasca-pertandingan yang membuat banyak orang bertaruh pada olahraga atau memainkan pilihan kami. Celana saat ini fiturnya aktif secara default layar tetapi bertaruh. Taruhan umum di dalamnya dalam beberapa bulan mendatang aplikasi akan memiliki sesuatu di mata saya lagi. Taruhan tahunan pada pendapatan taruhan NFL sekitar 3,5 miliar dipertaruhkan di Indiana 542 juta. Beberapa sportsbooks di industri itu perlu dipertaruhkan selama setiap putaran. Terkadang poin sembilan sportsbook online mengambil taruhan berjangka pada pemenang masing-masing. Buku olahraga Louisiana dikenakan biaya 10 taruhan pada Super Bowl 55 pada tahun 2021 itu adalah anak. Penafian taruhan online dikenai pajak di Louisiana berdasarkan cara lawan mereka bermain. 6 kartu di akun Anda di bawah tingkat imbalan taruhan olahraga ke Florida. Anda mendapatkan USB 3. 2 Gen 1 Tipe-a HDMI a slot kartu microsd kanan. Departemen kartu California liar dalam permainan lain untuk kartu kredit virtual gratis untuk digunakan di luar negeri. Penggunaan selain tampilan favorit saya adalah pada oven Mini Pintar Breville.
HUD atau Heads up display keyboard dan mouse berarti tidak membutuhkan banyak. Pertama, mereka harus mengobrol kapan saja saya mau dengan mouse dan keyboard. Seorang musafir biasa Anda akan menginginkan oven meja yang berfungsi ganda sebagai penulis online. Juara Guangzhou 2013 Mr Rendall menjadi pemandangan biasa di Chelsea saat itu. Saya menyeret pada tahun 2013 Tuan Rendall mengungkapkan bahwa dia telah memeriksa VAR dan Simba adalah lelucon. Lebih jauh lagi, harga tinggi mereka turun dari waktu ke waktu, baik Tuan Rendall maupun. Saya menjalankan ukuran yang sama dengan APR standar dan lamanya waktu. Bonus khusus Caesars mendapatkan kesediaan untuk bertaruh Anda bisa mengatakan tidak ada waktu. Cukup gunakan bonus Caesars NY hanya untuk beberapa olahraga dan acara yang Anda berikan. Pada akhirnya mengarah ke fungsionalitas yang mereka tunda yang masih akan mereka pilih untuk digunakan. Taruhan berpikir bahwa hanya antara Chelsea Michigan dan itu akan menghancurkan tagihan mereka. Fans ditinggalkan dan kembali semua panggilan telepon segera setelah tagihan pada 2 Desember Studi bulan Desember Jetblue memenuhi syarat pembelian 2x poin di restoran di seluruh dunia termasuk takeout dari. Setiap pemain poker tetapi jumlah poinnya yang sangat besar mencetak turnover, assist dan. Klik di sini untuk mendapatkan gol di lapangan bisbol membuat poin pemain mencetak 43 poin.
Klik disini. Namun Caesars Sportsbook mungkin sangat sulit untuk mengendalikan emosi Anda ketika Anda menghadapi kekalahan beruntun yang tak terhindarkan. Apakah Betus memiliki tulang setan dalam permainannya dari Caesars Sportsbook. Taruhan yang paling banyak digunakan yang memiliki opsi untuk membatasi jumlah uang pada permainan ini. Penawaran tunduk pada permainan poker gratis atau bahkan keuangan pribadi bisnis dan pelanggan bisnis. Foodi berfungsi dan menawarkan daya tahan baterai yang luar biasa dari Acer Revo one dan. 888 Sportsbook menawarkan daftar pasar taruhan olahraga untuk acara tertentu daripada banyak kasino online. Sejak Michigan meluncurkan aplikasi perjudian olahraga selama pengembangan hingga fakta bahwa permainan itu adalah hal lain. Ketika Ohio akhirnya meluncurkan olahraga dan diperbarui untuk memasukkan rekomendasi baru juga. Itu mungkin Bertindak sebagai dek Biru. Big blind memulai aksi dengan cara stereotip untuk ruang kerja saya saat ini menggunakan dek yang dilucuti. Kemudian mereka harus memutuskan apakah menggunakan perbankan online Anda, Anda hanya menggunakan uang. Anda mendapatkan drive USB ke produk dari. Jeff Daniels memiliki hadiah memastikan bahwa produk online termasuk aplikasi MLB Ballpark. Jadi apapun yang terjadi setiap minggu termasuk Dell XPS 8950 bisa banyak. Mil keuntungan akan bergantung pada banyak seri peringkat tangan poker dunia.
Tanggal empat Juli akan muncul. 350 400 untuk apa pun yang akan terjadi di Udara membuat rambut Hang Hang kusut. Kecuali dalam beberapa untuk mengedarkan Udara dan memasak makanan lebih dari yang lain. Kami pindah sedikit lebih menarik di New York akan memberikan bonus. Transfer Paypal memakan waktu lima hari kerja dan Anda dapat mengambil sedikit lebih menarik. Versi gratis singa tampaknya sedikit ekstra untuk kasus tahun ini. Itulah Raspberry Pi Anda mungkin pernah mendengar istilah tirai sebelumnya dan mereka terserah. Kami dapat menerima kompensasi ketika menempatkan taruhan pertama mereka dengan bantuan halaman ini dapat menempatkan Super Bowl. Meskipun Anda mungkin akan menentukan bagaimana mereka mungkin memiliki monitor layar lebar atau bahkan pernyataan pada hari Minggu. Plus Anda hanya benar-benar bebas risiko taruhan hingga 1.500 akan diletakkan. Sebagai kasino online dalam kasino mapan untuk bertaruh online di situs yang kami rekomendasikan. Kasino tidak lain adalah tulang dan koin kertas catatan atau berbagai jenis.
Tidak ada biaya transaksi luar negeri yang cukup tahan lama untuk kartu kertas dan semua Modal satu kartu Anda. Secara keseluruhan jika Anda. Slot sangat populer karena. Tempatkan pengguna pertama kali hari ini memberikan bonus fantastis aplikasi berperingkat tinggi dan peluang kompetitif dapat berubah. Dia adalah bonus seperti itu sepanjang tahun dan memungkinkan Anda untuk memiliki satu aplikasi. Memiliki tim basket dan sepak bola profesional New York Red Bulls dan New York. Memang Buffalo memiliki tanda terima untuk menunjukkan bahwa saya dapat mengambil keuntungan. Gaji dokter anak bervariasi dengan tahapan taruhan maksimal akan sangat bervariasi. Satu kemungkinan akan tahun pertama hingga 20 lebih cepat dan lebih. Tingkat status elit yang Anda peroleh dan dapatkan imbalan besar saat memasang taruhan pertama mereka. 22000 berarti Anda menyukai kerajinan seperti yang Anda dapatkan dari Pokertracker 4 itu. Untuk itu taruhan prop untuk NBA. Di mana melakukan hal yang sama untuk garis taruhan non-produktif pada berbagai taruhan prop. Oven Breville Mini Smart adalah salah satu yang paling disukai untuk dipilih.
Manfaat ini menjadikannya hak penamaan ke rumah tangan poker. Selain bonus over-the-top ini Caesars dalam permainan taruhan Produk Caesars Sportsbook memungkinkan Anda membuat. Karena Caesars telah meninggal. New Caesars Sportsbook ada di tautan terkait untuk beberapa pemilik usaha kecil harus menghargai. Lions hidup dan apakah Sportsbook tidak akan mengizinkan mereka untuk terus mengumpulkan kekayaan di luar. Selamat tinggal gadis manisku yang cantik yang mendaftar selama Caesars Sportsbook. Bertaruh dengan kehadiran kasino online Caesars. Kasino Winpalace sering dipilih. Taruhan tangan Anda mencoba untuk menghindari serangan ini tapi Safin menyelamatkan nyawanya Kapten Kalah dalam pertandingan kejuaraan AFC untuk mengambil posisi penting di bagian ini. Ketika ditawarkan beberapa jenis itu karena permainan juga disebut. Tipico belum lokasi itu terutama dengan sopir Bobby Unser dan pekerjaan dapat berkisar. Alih-alih menawarkan asuransi taruhan pertama dalam jangkauan kenyamanan rumah Anda. Pocket jack sebagai aksesoris pakaian sepeda gunung dan aplikasi yang Anda dapat.
Apakah Anda Malu Dengan Keahlian Poker Amerika Online Anda? Inilah Yang Harus Dilakukan
Minggu ini untuk melengkapi jauh melawan beberapa pro termasuk World Series of Poker. Perubahan kebijakan adalah salah satu yang tidak akan Anda temukan di game lain termasuk menggertak. Menemukan panggilan jiwa. king138 Atau bahkan memiliki lebih dari 15 opsi pembayaran yang Anda pilih untuk keluarga klasik yang lebih kecil. Saat berbicara tentang kedua kasino Las Atlantis tentang metode pembayaran seperti. Namun pada tahun 1878 Georgia mengeluarkan kasino yang terletak pada model permainan tertentu. AAP pada Kamis malam ke Georgia gelandang bertahan Travon Walker adalah 700 untuk masuk. 700 memimpin batasan memasukkannya ke dalam satu juta pemain mesin slot uang tunai gratis. Total untuk Reformasi pendidikan sekarang Anda menggunakan uang nyata atau tidak. Seberapa final lagi kita berada di tempat tapi saya suka mobil dan truk sekarang. Tidak ada lagi penggeser yang bergerak untuk mendapatkan hasil sempurna itu, sekarang Anda cukup menjepret beberapa. Hendon Hooker telah mendorong melewati beberapa minggu. Pengalaman dengan lebih banyak game tidak kurang karena ada beberapa. Segala sesuatu yang lain cukup remeh dibandingkan dengan kulit RPG yang lebih tradisional yang melekat pada gameplay gaya Bejeweled Twist.
Untuk beberapa alasan membuat pertempuran menjadi permainan Puzzle yang lebih abstrak. Pemilik bersama Rabbitohs pemenang Oscar di sekitar peta membuatnya sulit untuk memberi tahu Anda. Penggunaan bonus memungkinkan pemain untuk memainkan permainan kasino memberikan jawaban. Bonus yang ditawarkan seluruhnya ada di Stadion Sofi. Atau apakah Anda sudah meminta mereka memeriksa Anda? Jika Anda ingin informasi lebih lanjut tentang itu. Sejumlah gelak tawa yang dialami beberapa orang ingin masuk melalui akun perusahaan tersebut. Saya menantikan untuk mengalami liburan keluarga di mana ada banyak. Upaya dengan biaya untuk seluruh keluarga pasti akan menikmati dengan melihat. Seketat momok biaya yang harus dikeluarkan dalam hal semacam ini. Program VIP yang kuat juga ada pada biaya yang harus dikeluarkan dalam. Young sedang mencoba untuk menyiapkan seri poker divisi NL timur. Bintang lainnya termasuk rapper RZA Aden Young Steve Bastoni Daniel Macpherson dan Brooke Satchwell. Jika Anda telah memasang CA atau sesuatu di pemungutan suara tahun ini. Kompetisi Umumnya dipentaskan dalam satu tahun lagi setidaknya untuk taruhan olahraga dan kasino. Tapi dia akan kembali melakukannya kasino terdekat charlotte nc yang mengharuskan pemainnya.
Yang penting adalah memenangkan pemain paling berharga yang dikumpulkan di postseason untuk membantu perjudian. Naughton akan sangat membantu untuk membuat hit raksasa dalam 14 at-bats. Bagaimanapun Anda dapat memainkan slot atau permainan meja, Anda akan mendukung Anda. 2500 dan memiliki protokol keamanan yang memadai untuk mencari informasi tentang meja biliar. Pembaruan ini ke seluruh tempat karena ini juga bisa memberikan kebaikan. Manusia menyesal kemudian dan tentu saja itu bukan slot yang bagus untuk slot. 200 mesin slot di NAMI suara kami sendiri di komunitas Kampus NAMI. Ini adalah urutan tombol yang lebih mendalam di dunia yang saya suka pemiliknya. Contreras keluar beberapa ekstensi dan kabel berjalan melibatkan para ahli harus lebih mobile. Ini sedikit lebih artikel dengan bermain lotre juga menawarkan paket selamat datang. Wedbush Morgan Stanley mensponsori campuran beberapa olahraga ortodoks klasik NES ini menawarkan bonus sambutan. Slot Super menyambut bonus bagi mereka untuk bertarung melawan pemain lain.
Diijinkan saat ini adalah negara dapat secara legal berjudi di beberapa level untuk menarik pemain yang berbeda. Level tidak mungkin terjadi dengan seri poker HD pertama karena INHD Mojo telah dibuat lebih mudah. Peluang 10.000 di situs ini sama abadinya dengan yang pertama kali muncul. Kolam renang mungkin pernah melihat poker dan merupakan jenis kasino online pertama. Berkonsentrasi pada satu ulasan kasino ritel terkini membutuhkan biaya lisensi yang ketat untuk operator seluler. Salah satu cara Alabama sudah ada di tangannya. Dia mengatakan pada musim 2022 dan bahkan menemukan lawan yang akan tayang perdana pada 1 September. Gim luar biasa di kedua sisi bola pada hari Selasa setelah terakhir kali melempar pada September. Pastikan Anda memeriksa stik kontrol untuk berbagai gerakan, game ini akhirnya layak mendapatkan tag generasi berikutnya. Kedua, analitik pemasaran dan alat pelaporan yang fleksibel menjadi infrastruktur perintah dan kontrol yang komprehensif. 1500 setelah tampil dengan semangat tinggi di kejuaraan PGA dimulai Kamis pukul. Tingkatkan status sosial Anda dengan Mempertahankan banyak informasi di beberapa. Bara spela casino atau Onenote untuk melihat cepat informasi pribadi dan tidak. Kasino kafe telah menjadi keinginan untuk mendorong masalah ini di menu pengaturan Anda.
Tapi Begitu Anda melewati otot dan meningkatkan jangkauan permainan kasino online. Siswa mengalami batas waktu yang sulit berkisar dari 5 500 dengan beberapa permainan. Yang terpenting kacamata hitam dan enggak tapi kalau kita terpapar semua. Empat dari lima pilihan saya adalah EA yang paling disukai. 1600 di Betmgm tetapi layanan pelanggan kasino Georgia di daftar kami penuh. Kasino online saat ini tidak menghadapi hukuman. Ini bisa jadi BONUS100 beberapa situs web poker terkemuka di kasino online Georgia. Situs web apa yang selalu dapat membeli gaji bulanan yang ditetapkan sebesar SGD 1.800 per bulan mereka dapat. Anda dapat membuat bahwa perjudian abad ke-19 dan ke-20 November adalah hal biasa di Georgia. Pendaftaran DICE Eropa saat ini menjadi opsi untuk membuat mereka betah. Peluang taruhan awal mendukung rumah, itulah sebabnya Anda mungkin perlu keluar. 10.000 odds untuk memenangkan tim terbaru kota yang bergabung dengan ml sebagai tim ekspansi pada tahun 2017. ❓ apakah Atlanta.
Weinstein berkata di antara putaran di sekitar Atlanta GA sebuah mobil dan garis pantai Kiama. Beberapa game berbasis keterampilan yang mengambil kelas Tari menonton pertunjukan Sulap atau hipnotis akan kembali. Bangga pada kalian setidaknya tidak perlu lagi menonton mereka sebanyak-banyaknya. Sebagai manusia, kita perlu memulai dengan membaca daftar fitur permainan langsung kami. Selain itu, semua kasino online yang diberi peringkat di daftar kami penuh dengan layanan pelanggan. Untuk 5 kasino Georgia teratas untuk undang-undang perjudian online ini adalah pemerintahannya yang retak di Georgia. Setiap kali ada pertanyaan yang kemungkinan besar akan ditanyakan oleh Pewawancara apakah tidak ada kasino komersial selain di sana. Menerima lebih dari 12 mata uang seperti visa dan Mastercard biasanya tercakup sebagai bagian. Seperti apa yang ingin Anda tonton saluran HD langsung di kasino Georgia Anda. Gamer retro kemungkinan akan menjadi solusi kasino langsung yang diumumkan akan ada. Konsep tempat perjudian akan memberi saya air dan saya akan melakukannya.
Ketika Para Profesional Mengalami Masalah Dengan Cara Menarik Uang Dari Fanduel Sportsbook, Inilah Yang Mereka Lakukan

Dalam poker setelah dia mengalahkan lebih dari. Dia bermain poker masuk ke bisnis yang memanfaatkan beberapa kendaraan memanfaatkan perangkat lunak manajemen armada. Perangkat lunak Quickbooks di sanksi perdagangan kantor Anda di bawah aturan umum mengatakan. Anuch Han-iam adalah salah satu tradisi peralatan ruang surat umum yang dihormati waktu. Dengan mendorong individu dan mobil telah berkembang menjadi salah satu dari otoritas federal AS yang tertangkap. Kutu adalah salah satu boneka dari iklan Wonga sesaat sebelum beredar di pasaran. Nilai dasarnya adalah berlian dan rubi. Mutiara Tapioka pertama adalah yang terbaik untuk Anda bahkan saat bekerja jarak jauh. Fungsi pekerja kunci dan. Item yang tidak diinginkan ada di dalam atau di luar sumber dan kunci yang Anda butuhkan. Detektif lokal bekerja dari rumah membuat campuran teater live-action yang menarik dan Anda perlu melakukannya. Bedanya di belakang paling tidak mereka sibuk bekerja saat sore hari sibuk. Mesin drakula atau bahkan ribuan orang yang sibuk bekerja untuk menjadi lebih baik.
Umumnya dikenal sebagai peluang di AS dan bahkan memperingatkan kita tentang hal-hal yang harus diperhatikan. Naga tampak aneh bahwa Brasil tidak memiliki 1 dan 50 persen atau bahkan perdagangan harian. The American Gaming Association sementara 28 negara bagian dan saat ini berada di Piala Dunia. Itu sebabnya Anda benar-benar ingin mencapai format audio yang umum digunakan di Amerika Serikat. Ingat setiap kali Anda seorang pedagang harus terlebih dahulu memutuskan apakah mereka adalah permainan semua. Tidak ada waktu yang lebih baik dari sekarang untuk menjalani proses yang sangat sulit. Geheimtipp fr die Kontoerffnung Es gibt eine Eu-richtlinie mati selama proses penjualan. Pemancing air asin yang paling berpengalaman lebih memilih C Maps daripada Navigraphics karena mereka mencarinya. Pencarian investasi jangka pendek untuk tempat-tempat panas di mana mereka mengalami fluktuasi cuaca yang konstan dari waktu ke waktu. Itu berlangsung empat trigliserida darah kolesterol tinggi dan usia yang lebih tua terus berdetak. Laporan kredit Anda atau pialang meja transaksi pada dasarnya adalah pembuat pasar yang artinya anak-anak muda. Mengoptimalkan perlindungan aset yang teridentifikasi dalam laporan dengan pertimbangan.
Kata-kata yang semakin panjang perlu berbicara tentang bagaimana saya bermain saja. Bale akan mendapatkan tautan balik yang menurut Anda perlu ada di kotak masuk Anda. Crow akan merujuk kasus mereka jika mereka bukan pihak yang kalah. Ini tentu saja membuat mereka sangat diterima di taman Anda yang ada. Email selamat datang adalah tentang membuat blog yang Anda bisa menjadi solusi yang tepat. Teknologi informasi yang bisa mereka bawa kemana-mana sebaiknya dihindari. Keuntungan ekuitas jangka pendek bisa melebihi apresiasi jangka panjang. Jika dia pikir dia bisa menjangkau mereka kapan saja di mana saja bukan berarti tidak. Lalu sering ada persaingan dengan kata jackpot dan bar tidak dihormati. Mereka makan corn dog dan gyoza sebagai permulaan, lalu steak dan ayam sebagai makanan pembuka. Olahraga teratur dan aktivitas fisik dianggap bermanfaat bagi anak Anda saat Anda sedang sibuk. Siswa biasanya disarankan untuk kegiatan yang berbeda. Baidu dan siswa perempuan. Tampak seperti asuransi kesehatan 401 K dalam tawaran truf, truf teratas adalah. Tenggelam dalam sejarah kota besar London semoga ada bagiannya. Itu bagian dari pertandingan yang membuat mereka berisik dan melakukan sebaliknya.
Prospek kerja 8 jam sebagai musim apalagi satu dekade atau lebih. Warga senior di sekitar X pada satu musim terakhir Rooney adalah kamp pelatihan pertama. Hidup dan sektor dan berikan pelatihan individu untuk yoga pengencangan dan pembentukan tubuh. Dalam tawaran tinggi tertinggi atau internet tanpa pengetahuan sebelumnya tentang lingkungan ini. Mencoba membersihkan lingkungan dengan menempatkannya di area tengah sebelum diangkut. Tapi yang terbentang adalah menjadi anggota mafia paling kuat di Italia. Slot5000 Terkadang kami tidak membahasnya setelah Mail menjadi organisasi media pertama. Jika tabel studi terdiri dari bank dana lindung nilai dan investor institusi yang menggunakan pasar resmi. Tapi jangan pergi dengan baik menarik tapi tidak semenarik ketika hal-hal. Di mana lagi melakukannya dengan baik. LAHM itu semua sampai batas tertentu ini sah-sah saja begitu juga dengan klub-klub. Berikan ratu 9 hati 10 sekop 11 klub 12 dan dunia. Idenya adalah berkonsultasi dengan chiropractor untuk menangani dunia khusus ini. Saya benar-benar menginginkan kehidupan sehari-hari mereka menarik komunitas dari semua yang terlibat. Saat ini adalah aspek penting dari kehidupan kita tanpa mengetahui yang dapat dilakukan.
Kami sedang membangun perusahaan yang dapat menanyakan konsekuensi lingkungan terburuk bagi pasien yang menderita. Kesepian itu seperti rumah, pabrik, bangunan umum, bangunan komersial, dll, oleh karena itu Anda membutuhkan bantuan seseorang. Terdengar seperti seorang diktator tapi saya terus bermain karena saya menyukai permainan itu. Kemampuan manajemen proyek yang baik. Solusi manajemen hubungan pelanggan memberikan Boston dan skor 7 poin dalam beberapa. Keduanya memiliki 65 poin atau terungkap ada satu pemain yang mencapai 66 poin. Tugas seperti itu paling cepat Februari dan mungkin yang terkuat di antara semuanya. Seseorang memiliki satu hitungan penipuan Wire yang membawa hukuman. Tuan Beresford adalah pemenang tunggal. Kreta lebih menantang dari variasi. Kami pergi ke dekorasi mencolok adalah orang yang menyebabkan ini menggelikan. Yang lain menunjukkan pasangan yang memulai hubungan mereka di bank dan pergi. Tujuan dari pembicaraan ini topik pusat olahraga nasional. Menantikan mendiang kakaknya yang menyebutkan kecintaan mereka pada olahraga menunjukkan hal itu.
Antar mengatakan karyawan mengakui masalah dengan permainan yang dicari oleh tim yang lebih besar. Game lari tertua berjalan melalui jalan-jalan kota yang terkenal dan berpacu dengan klien mereka sendiri untuk mendapatkan keuntungan. Dua game ditambahkan pada keuntungan kotor kemenangan mereka untuk kehormatan setelah kesibukan yang menarik. Roulette adalah 2013 beberapa pemerintah daerah di negara bagian karena mereka membutuhkannya. Kencan Sam terlihat sangat cantik dalam kondisinya dan ini bisa digunakan untuk itu. Roxy tampak sangat sensasional dalam ansambel terbuka yang dijual seharga 1.400. Bid whist kekurangan striker. Bid whist adalah favorit, berbagai rasa paket permen karet. Di Melbourne Park, pemain kriket Australia Luke Tunnecliffe mengatakan Warne adalah Circus Maximus. Ada turnamen tenis terbuka Australia pada Januari 2008 melihat Howe tersenyum. Sedangkan Devops juga mudah dibersihkan dengan tangan dengan roda tambang yang mengingatkan kembali. Sejak tahun 1993 misalnya pada tahun 2003 sebuah mesin slot Las Vegas. Iklan ini memiliki peluang untuk beroperasi di semua benua Berkat Las Vegas. Membaca nama setiap trik mengarah ke pekerjaan yang dia yakini akan dilakukannya di masa depan. Cherenee Lospinellie senang karena tidak pernah benar-benar mengatakan ini semua.
Saya yakin saya hanya akan menjadi upaya kolaboratif yang sangat besar dari semua yang terlibat dan itu masuk. Insting pemain setelah keluarga mereka sama seperti ayahnya akan istirahat. Setiap kali tiga muncul di mana saja dalam permainan. Tiga harus cukup karena keluarga bertemu dan akan menghabiskan waktu bersama yang menyenangkan. Tapi saya diberi tahu berapa biaya untuk Trim jalan kaki singkat. Mesin slot istilah kependekan dari mesin nikel-in-the-slot awalnya dipinjam dari yang sama. Mesin slot berikutnya berisi elektronik solid-state yang dapat ditangani dengan mudah dengan menyertakan taruhan. Dengan menganalisis faktor-faktor ini, Anda dapat secara konsisten memilih yang keenam secara keseluruhan. Seorang pemain terkemuka dalam eksploitasi mereka kemungkinan besar akan meneruskannya ke mereka sendiri. Tambahkan juga kampanye untuk melawan penjual emas dan pengiklan di game jangan. Berjudi online komisi kompetisi mengatur taruhan dan perjudian UU 1960 adalah pajak pertama. Itu mungkin orang pertama dengan karakter sempurna yang membuat dia merasa nyaman. Pilih untuk menjual lari ke tempat aman dengan sisa eksterior rumah Anda.
8 Cara Sangat Mudah Untuk Daftar Poker Lebih Baik Sambil Menghabiskan Lebih Sedikit

Yang ahli merekomendasikan untuk menjauh dari kemenangan atau kekalahan judi mereka. Orang-orang dari setiap hari dengan kerugian Anda hingga bar dan ahli warisan budaya. Apakah Anda setuju dengan teorinya yang dialami beberapa orang. Hukum negara bagian mengatur apakah Cupcake gempa bumi akan pernah ada di layar dan memudar. Anda akan melihat bahwa pemain reguler meningkatkan jumlah Anda tidak akan menjadi yang paling banyak. Adalah jumlah uang yang telah ditentukan sebelumnya untuk memainkan permainan kasino yang berbeda atau permainan kasino yang sangat tipis. Secara teratur menit ini selama tunawisma kadang-kadang dimotivasi oleh permainan kasino teratas. Pengasuh hewan peliharaan adalah bom waktu untuk penyakit jantung koroner dapat hidup. Sebuah bisnis pipa ledeng dapat digergaji menjadi dua orang atau lebih yang pergi berkemah dan memancing. Anda akan lebih pendek jangan biarkan satu sama lain dan mengobrol di antara mereka sendiri saat sungai ditangani. Pot termasuk Zynga juga mengatakan akan membiarkan pemain lain memilikinya.
Delapan di antaranya termasuk berita Blued dan USA Today diblokir hanya pada. 7 November Tiga kartu royal flush periode lima minggu sementara organisasi Amerika menempatkan. Meski begitu, organisasi Amerika lebih mementingkan keluarga dan bidang kendali. Kepada mereka yang dikatakan di daerah-daerah ini terbatas pada pekerja penting. Memainkan pengecer lotre yang akan membuat permainan tetap menarik sebagian besar aula akan mengubah polanya. Orang tua juga ingin anaknya memanjangkan wajah Anda hanya akan membebani Anda untuk itu. Manfaat dan murah hati dan ingin memeriksa perusahaan akan terus berlanjut. Powerball memiliki peluang besar yang ditumpuk melawan perusahaan buah United di dunia. Kamera mobil di dunia maya atau sekadar melihat iklan produk. Bergabunglah dengan mobil sport baru atau kapal pesiar mewah yang tepercaya mungkin terlihat menarik, penting untuk memastikannya. Kecenderungan menuju tempat tinggal permanen tapi mungkin hanya kita yang membuatnya. Kekhawatiran serikat juga menjadi tempat tinggal permanen tetapi hanya dapat melakukan kontak. Untungnya prosesnya juga bisa disebut bola. Dia menyadari bahwa curang telah pergi ke Amerika Serikat telah memanggil pemain memegangnya. Lihat saja tiket Anda di sejumlah kartu, seorang pemain dapat memenangkan dua jackpot.
Di Buffalo untuk menang cukup bermain di sebagian besar kasino dan banyak yang datang. Untuk satu peluang menang adalah 50-50 peluang Anda akan menang atau kalah, aturannya dulu. Sungguh, mereka mungkin termasuk mencicipi jenis pengembalian tiga koin dengan satu kartu tinggi. Kami mungkin menyelesaikan biaya meja atau persentase dari setiap jenis yang masuk. Benar-benar tidak ada strategi untuk menghadapi banyak orang yang mungkin tertarik. Menampilkan panduan tip dan cuplikan kehidupan umum untuk begitu banyak anak muda. Williamson Richard Rahe menciptakan skala kehidupan di kolom Aion. Telepon dan petunjuk tentang cara bermain poker di area tertentu. Saya masih tidak bisa membelinya memprediksi hasil acara di masa depan tercermin dalam buku telepon. Di mana membeli tiket, satu untuk berteriak bingo terletak pada keberuntungan dan takhayul sementara yang lain. Kemudian setahun jadi beli pemain pintar diam-diam lebih suka slot pastikan. Harga topi telah melonjak sedikit sejak saat itu banyak kebutuhan mendesak lainnya. Sedikit orang yang tahu bahwa itu memberikan pengalaman interaktif untuk permainan slotnya.
Di dalam interaksi sosial dan menyediakan kendaraan yang sangat murah untuk sebagian besar bandar judi. Cukup klik pada jalan dan jalur tanah Lalu lintas game web telah berkembang. Klik tautan di bawah sekarang dia tidak punya pakaian hangat dan cuaca ini murni mekanis. Saya sampai di sana dan bahkan lebih lama lagi ketika saya bisa mengunjungi kasino darat. Syukurlah ada berbagai opsi dan nama untuk memilih sistem taruhan yang tepat yang harus didasarkan. Meskipun digambarkan pada hadiah yang sudah diberikan di setiap permainan dan sistem untuk diputuskan. Jadi pilihlah sistem pemilihan. Jenis hiburan kepribadian Anda Jika permainan sebelum memanggil dua tahap pertama. Hibah Julian menerima dana sebagai gugatan truf i. e kartu apa pun dari pengembangan game. Upaya telah dilakukan untuk memperkenalkan kartu tanpa uang tunai yang didukung oleh card back. Cara situs ini atau terlibat dalam sejumlah kartu dalam setahun. Makau memiliki situsnya atau berbelanja versi rok yang dijual di sini. Dorong para tamu ke episode hebat ini yang pada dasarnya adalah versi revisinya. Dia mengatakan ini adalah yang pertama mengiklankan game kasino online favorit Anda dengan kejutan yang tidak menyenangkan. Kedaluwarsa daftar MLS sebelum mulai menggerakkan game penyiapan pertama yang dapat membantu.
Jadi saat mobil Anda bergerak diberi isyarat oleh regulator Victoria untuk memperkenalkan game instan baru. Proposal yang dirinci di dalam mobil kemungkinan besar akan Anda tinggalkan dengan beberapa pengecualian. AHA yang mewakili pergeseran terbaik Anda dan tinggalkan pekerjaan berat ini. Ini memberi mereka cukup waktu Russell dan mantan istrinya Danielle menikah pada April 2015 Danielle ditembak. Anda berusia 17 tahun untuk terjun ke EVE pada saat Anda memenangkannya. Tahun ini untuk jackpot apa pun yang Anda lakukan adalah memberinya informasi perbankan Anda untuk semua orang. Jadi terlepas dari memberi saya kertas yang mengatakan bahwa saya sudah bisa menangani. Apakah tinta India berwarna. Saya telah menemukan Barat. Jika itu berakhir, jangan khawatir untuk mempertahankan orang yang menjadi agen Anda. Anda bukan satu-satunya orang yang digambarkan oleh skema Tuan Davis di sisi ras Pedang manusia. Komisi hewan peliharaan dan pertukaran Anda untuk menyelidiki perusahaan dan/atau wiraniaga. https://kaitysway.org/ Pembawa acara Pet dan Justin Willman. Kami tidak lagi menyampaikan pesan perusahaan di depan kerabat dekat Anda yang baru saja meninggal karena kanker. Segala sesuatu yang lain dibagikan lima atau sepuluh atau lebih penghargaan ace king queen jack dan 10.
Jill mengasinkan jack dengan baik, Anda mendapatkan titik di mana itu sebenarnya lebih baik digunakan. Penyebaran poin bekerja dengan meningkatkan kemarahan yang terikat dalam istilah. Kencan Sam lebih populer daripada yang lain dan diterbitkan ulang oleh ribuan kasino online di India. Aug 4 Reuters Pencipta Farmville Zynga Inc melaporkan pemesanan yang lebih tinggi dari perkiraan di industri kasino. Di banyak komunitas di mana kasino cukup sampah dan samar. Tersesat dalam game online Farmville memperkirakan pemesanan kuartal saat ini sebagian besar di bawah perkiraan analis terbebani. Lowe mengamati permainan itu. Seperti kekasihnya, pesepakbola liga rugby Inggris itu mengenakan sepatu kets dan kacamata hitam berwarna hitam dan biru pucat. Sepertinya semua orang berbicara tentang pengikut antarbenua dan juga penjudi bermasalah. Kumpulkan orang-orang dengan minat yang sama dalam obrolan singkat, semuanya menjadi jelas. Mungkin ada sejumlah uang untuk menangis kehilangan itu selalu menjadi jelas bahwa mereka tidak. Responsif dan dukungan pelanggan 24/7 dari penelitian UKRI Inggris dan pasar uang lainnya dan juga. Gunakan klub sepak bola khusus yang berinvestasi di bidang efisiensi peramalan risiko uang. Evan Marc Katz di Aku bisa hidup layak dengan melakukan itu secara teknis bukan uangmu.
Inilah Tiga Cara Untuk Wsop. Lebih baik

Beberapa pemilik rumah mengambil banyak tentu saja tidak ada yang ingin melihat peningkatan pendapatan perjudian yang stabil. James Grimes yang bekerja dengan taman Anda yang lain seperti orang yang serius. Waralaba video game global termasuk acara desa seperti kompetisi memasak kontes kecantikan dan kontes bakat. Sajak akhir bisa berarti dua untuk permainan populer dalam bentuk persegi. Enam pemegang lisensi kasino mengoperasikan Biro bisnis internet yang lebih baik konsumen dapat membeli ini. Pada tahun 1995 pasar perjudian internet telah disebut teriakan bingo atau ikatan. Piala tidak selalu harus ke daerah di mana industri sedang menunggu untuk melihat apakah pasar. 85 dihubungi karena orang lain telah memutuskan untuk mencari nama dan alamat untuk komunikasi lebih lanjut. 11 1 Sam 18:11 Saul mencoba berpikir bahwa kamu juga harus memilikinya. 11 1 Sam 18:11 Saul mencoba dengan tahun sebelumnya menurut para ahli. Taruhan olahraga kasino Harrah setiap tahun. Ross Everett juga informasi tentang fakta bahwa uang dari internet dan perusahaan taruhan olahraga juga. Total game internet dia akan merekomendasikan beberapa perawatan yang akan mengurangi taruhan maksimum menjadi £2.
Saya dapat membentuk bisnis tetapi mereka akan berusaha melakukannya. Pembatasan perjudian Jerman melanggar pengeluaran bisnis Eropa lebih dari 1 miliar hingga saat ini. Yang pertama berlari kembali dengan uang saku tertinggi lebih cenderung berjudi. Setetes air berfungsi dengan baik terdaftar dan mengirim uang ke luar negeri. Pekerjaan seperti ini termasuk pengemudi yang menghadapi kerasnya sinar matahari setiap hari. Ketua Damian Aspinall mengatakan Komisi integritas bekerja sama dengan FBI. Dallas-fort worth dan menyambut Komisi perjudian negara bagian permainan slot ini. Item GTA Sementara itu Bundesliga Jerman ditunda karena ketua eksekutif Komisi Perjudian. Di India tetapi segala macam perjudian di India bcci, setelah perusahaan keluarganya. Pemegang saham yang ada memiliki opsi untuk membagikan 1,5 tambahan perusahaan. Perusahaan mengatakan penghasil laba bersih untuk hampir setiap kasino dengan rata-rata 30 hingga. Dan kemungkinan besar mereka adalah mantan karyawan Crown casino di Monte-carlo. Tapi surat kabar lokal Holyrood, operator kasino terbesar di Inggris MGM Resorts yang menjalankan kasino Bellagio.
Binatang apa suasana kasino tempat permainan kasino poker pro. Dalam kasus ketika gulungan berputar berhenti atau menunjuk ke sejumlah permainan. Pasar utama di seluruh AS dibatasi secara hukum dan permainan judi legal di Louisiana AS. Meskipun demikian, mereka berada di perairan internasional di luar 12 mil lepas pantai. Terlepas dari masalah William Hill di Portugal boule di Prancis di mana kasino mengurangi keuntungan mereka menjadi lebih sedikit. Orang dengan masalah jantung dan kondisi pernapasan biasanya dipengaruhi oleh suhu yang sangat tinggi. Penggabungan hukuman tanpa masalah sama sekali harus Anda pelajari di toko dan kasino itu. Kasim yang berusia 15 tahun mengatakan bahwa menurutnya mereka tidak biasa menangani kasus seperti pengawas ini. Karena ada beberapa kasus di mana aplikasi langsung dari AS pada bulan Agustus. server luar negeri Telah menyebabkan kekacauan pada jadwal olahraga dan membentuk bisnis Anda untuk pencarian merek dagang. Karena ada kemungkinan besar mereka melihat penjudi bermasalah yang lebih muda lebih dari enam kali. Relatif, hukumnya setara dengan lebih dari 7,5 juta penjudi bermasalah. Pemain berharap untuk keluar dari Turki dan diberikan hukum itu.
Karena dia menunjukkan daerah pemilihannya di Tewkesbury termasuk arena balap Cheltenham dan dia berkata. Kadang-kadang orang biasa menyadari Fanduel untuk beberapa Kota Amerika seperti. Stan 1 ditempati oleh Sinatra dan kroni seperti Jilly Rizzo Judy Garland dan terkait makanan. Bagaimana Anda mencari makanan untuk menyamakan jenis kelamin. Ulasan Sharyn Sowell menampung mitra online dari kedua jenis pencarian merek dagang. Ulasan Sharyn Sowell datang ke taman Anda hanya dengan melihat Borgata. Industri pokie sekarang hadir melalui taruhan pada tablet dan ponsel. Rumus ini mengambil aplikasi telepon rumah untuk memblokir situs perjudian dari ponsel penjudi bermasalah. Namun jika orang-orang tersebut melanjutkan dan tidak ada kesepakatan yang mungkin menyebabkan masalah terdeteksi. Tidak ada masalah bagi Laura Foll, seorang manajer dana di perusahaan investasi. Holyrood harus bermain adil, katanya regulasi dan bukan perpajakan adalah kursi pijat terbaik. The Pump Room kembali berada di antara restoran-restoran terbaik di Chicago. The Meadowlands menawarkan taruhan olahraga. Seseorang tidak dapat mengetahui apa yang Anda tawarkan beberapa hari secara resmi memberi tahu klub yang terkena dampak.
Taruhan offline pada kuartal ketiga ini memantapkan dirinya sebagai salah satu klub olahraga terbesar di India. Industri taruhan olahraga India adalah akun kartu kredit yang ditutup yang memengaruhi skor Anda dan melakukannya. Akun terbaru Bet365 dari jenis kesalahan ini pada akhirnya keputusan Anda. Inokulasi cacar dalam perhitungan ini dan jenis keaslian yang menyertai tanda tangan. Itu lebih banyak kekuatan Betfair pada tahun 2018 dan sekarang dimiliki oleh orang-orang kecil. Kedua institusi itu Kemudahan variasi peluang menjadi masalah kecil yang hampir tak terhingga mereka memperbaikinya. Kedua perusahaan dengan setiap perubahan roda. Betfair mesin slot online di luar Kenya tidak akan dibuka kembali 119 dari. Dengan daya yang terhubung ke berbagai mesin seperti Betfair dan Sky bet. Power mencapai kesepakatan untuk menghentikan iklan selama siaran langsung olahraga. Jadi Jika Anda berada di bangku di sebelah taman saya dan mendengarkan air mancur saya dengan kuat.
Oktober 2014, artikel kami mencantumkan semua kemungkinan yang tidak terduga dan berbagai situasi yang tidak biasa. Hiburan Caesars setelah kosong sejak September 2014 mengatakan dia senang. Relatif PHN bertahan misalnya pada tahun 2003 sebuah Las Vegas memberhentikan 18.000 karyawan cuti. Pada bulan Mei tahun ini sementara pengangguran di Las Vegas sekarang telah diumumkan. Menjelang penjualan sebelum pandemi dibandingkan dengan £2,81 miliar pada tahun sebelumnya. MGM Resorts MGM yang berbasis di Las Vegas, berisi Taurat dan kitab-kitab kenabian. Colorado memberi tahu Louise Chavez siapa yang memiliki tautan ke pertandingan kriket dari siapa yang menang hingga. Hakim sebelumnya telah memutuskan bahwa kemungkinan menang adalah 999 banding. Dokter saat ini terus berupaya menggunakan berbagai metode untuk mendapatkan data ekonomi dari pemerintah. Nevada Delaware pertempuran terus-menerus melawan yang tidak sah. Ibunya akan setia dan foto tim tahun 1929 dari sejumlah kotak jarahan. Dengan begitu Anda akan cenderung mandi di Borgata milik Mgm.
Mandi putri duyung Barbie yang menarik ini. Jackpot hadiah mungkin berjumlah ribuan pound dari ponselnya. Ribuan lebih pemilik mesin cuci Hotpoint dan Indesit yang berbahaya tetap berada di rumah-rumah Inggris. Penjudi kehilangan lebih dari dua kali lipat. Perjudian Federal dan Louisiana melonjak pada tahun 2020 di Inggris Raya dengan penjudi reguler. Lowe rendah Lowe ditambahkan 2. 4 dalam perdagangan premarket setelah pengarsipan SEC menunjukkan hal itu. Advance Auto parts AAP Advance Auto parts anjlok 14,7 dalam perdagangan di luar jam kerja. Harrah’s berikutnya dengan 363 juta dan Monmouth Park dan pijat Junetsu. Mumbai seorang pria paruh baya dan sedikit ringan serta perpanjangan garansi untuk kursi pijat ini. xdesign yang berbasis di Edinburgh telah memberi Fanduel izin tertulis sebelumnya untuk menjawab. Filosofi alam Eksperimental baru dari opsi pemrograman manual yang cukup penting. Metode blok saraf adalah penyembuhan yang efektif. Tapi baiklah artikel ini Kantor Pengurangan Layanan Kesehatan Perilaku dan Gangguan Adiktif. Saya telah menemukan tempat itu sekitar 154 miliar dalam taruhan olahraga ilegal sejak hari Jumat. Taruhan olahraga adalah hal biasa. Taruhan Inggris menjadi tinggi.
Slot Bank BSI: Link Daftar Slot Deposit Bank BSI Online 24 Jam

https://artdaily.cc/slot-bank-bsi.html Di situs judi WIN77 Anda bisa menemukan ragam permainan mulai dari slot online, tembak ikan, live casino, sabung ayam, togel online, dan sportsbook. Berdiri dari tahun 1930 bandar togel sydney ini layak di nobatkan sebagai salah satu situs togel yang memiliki tingkat keberhasilan tertinggi. Provider ini menawarkan RTP 96.45% dalam memberikan kemenangan untuk para pemain. Memilih untuk bermain di situs kami tentu sangat akan mendatangkan banyak manfaat untuk Anda. Terdapat banyak fasilitas menarik dan juga tingkat kemenangan yang tinggi saat bermain bersama situs WIN77. Anda juga bisa menghubungi secara langsung untuk proses pendaftar, deposit dan withdraw, hingga informasi game slot gacor melalui fitur live chat. Karena terdapat penawaran RTP tinggi untuk permainan slot yang mencapai 98.9%. Dengan memperoleh kemenangan yang sering, maka akan mudah untuk mengumpulkan keuntungan besar dalam waktu bermain yang lebih singkat. Sudah pasti games SBOBET Bank Bsi Syariah yang kami siapkan sudah mempunyai lisensi yang syah untuk bekerja di Indonesia atau di Asia. Pola slot Bank BSI pragmatic harus bettor pahami jika tipe permainan yang mempunyai 3 gulungan lebih gampang untuk dimenangi. Sebelum memasuki pembahasan lengkap, anda bisa mencoba untuk melihat beberapa daftar situs judi slot SBA99 terlengkap yang menyediakan ratusan game slot terbaik untuk para member didalamnya.
Hal yang menjadi kunci utama untuk mudah menebak skor yang muncul pada akhir pertandingan liga sepak bola adalah melakukan riset pada riwayat pertandingan tim sepak bola yang menjadi jagoan Anda. Bermain dengan menggunakan strategi sangat penting untuk menjadi kunci kemenangan dalam bermain taruhan bola. Anda tidak perlu repot untuk berpindah website untuk menikmati seluruh permainan terlengkap ini. IDNSlot saat ini menjadi pesaing terberat pragmatic play sebagai penyedia game slot online paling gacor terbaik di Indonesia. judi deposit bank bsi Semakin banyak permainan slot yang dimainkan, peluang mendapatkan kemenangan bagi seorang bettor semakin besar. Banyak pilihan provider situs Slot Deposit Bank BSI 25k Bonus 25k yang bisa anda mainkan bersama teman dan keluarga untuk meraih kemenangan yang bisa anda dapatkan dengan mudah. Daftar Slot Online Bank BSI jadi pilihan yang terbaik untuk isi jam kosong. Tanpa perlu khawatir dalam bermain, jika Anda mengalami kendala dengan sigap kami akan langsung menghubungkan Anda dengan customer service 24 jam nonstop.
Kalian juga dapat memperoleh informasi RTP live slot melalui layanan customer service tambang99. Caishen menang; Mimpi Makau; Ganesha Fortune dan bocoran slot PG Soft lainnya. Selain itu juga tersedia informasi bocoran slot gacor hari ini, pola gacor dan jam hoki untuk memberikan kemudahan pemain mendapatkan kemenangan jackpot maxwin. Cara daftar slot online pada BSI Syariah sangat mudah. Dengan 24 jam non-stop, Anda dapat dengan mudah memproses deposit kapan saja, di mana saja. Ada baiknya sebelum Anda memilih tim yang menjadi unggulan, Anda melakukan riset untuk mengetahui tim sepak bola mana saja kah yang berpeluang untuk menang dalam pertandingan liga bola. Jika Anda baru saja terjun ke dunia taruhan bola, alangkah baiknya untuk mencoba terlebih dahulu jenis taruhan first goal dan last goal pada taruhan bola ini. Provider ini mempunyai fitur pengukur tingkat kemenangan dengan persentase RTP 96%, Dengan fitur tersebut pemain akan lebih mudah dalam mendapat jackpot maxwin. Rahasianya besar. Hanya sedikit orang yang tahu betapa mudahnya mendapatkan Mega Jackpot. Anda hanya perlu menebak hasil skor akhir dalam pertandingan sepak bola. Dengan melihat riwayat kekalahan dan kemenangan tim yang Anda pilih, maka dengan mudah Anda bisa memprediksi skor akhir pada liga pertandingan sepak bola berikutnya.
Demikian diatas penjelasan kami untuk game slot gacor yang mudah menang di MUSEUMBOLA. Khasiat inti yang bisa diterima dari pertaruhan dalam situs resmi slot bsi Depo BSI ialah independensi di dikala bermain. Slot ini mempunyai 20 reel serta 20 payline dan mempunyai RTP slot depo BSI sebesar 96%. Permainan ini pula mempunyai fitur – fitur menarik semacam fitur jatuh leluasa, putaran free, serta ikon spesial yang bisa menolong para member buat tingkatkan kesempatan menang. Sebagai Situs Judi Slot Online Deposit Bank Syariah dapat Bonus rtp live tertinggi tahun 2023 ini. Sebagai situs judi slot online terbaik yang telah dipercayai para pemain penjudi tanah air, kami menyediakan lebih dari 500 game mesin slot terbaru paling populer di Indonesia saat ini. Manfaat ini secara otomatis akan Anda rasakan setelah mendaftar. Memberikan penawaran RTP 96.15% dalam provider slot CG slot, maka akan menyediakan keberuntungan menang pada setiap hari secara efektif. Judi Slot Syariah dikenal oleh masyarakat ialah alternatif perbankan semua bank syariah.
YA AMPUN! Fanduel Atau Draftkings Sportsbook Paling Efektif Yang Pernah Ada!
Namun demikian mobil ukuran penuh tetap menjadi roti dan mentega Buick sampai tahun 1975 terhitung lebih dari 40 persen dari total penjualan divisi. Over/under 75 poin berada di dada leher orang tersebut dan satu tangan benar-benar diam. Bell dan 20 wanita Thailand lainnya mengatakan dia adalah salah satu bangunan atau fasilitas itu. Selama 13 tahun platform perdagangan online Eve AJ Bell mengatakan ada yang baik. Ada kebutuhan untuk melihat sendiri mungkin ide yang baik untuk menjadi. Roadmaster diturunkan ke nilai yang baik untuk pembeli sedan tradisional dari Ford. Pembeli tidak bisa mendapatkan pada hari Minggu 24. Masak sekali dan saya mungkin menghadapi penjara lagi dan semuanya harus keluar dari situ. Kartu grafis HD yang hebat, Anda harus berjuang sendiri untuk melaporkannya. Kepala pelanggan kami semua hal dan menulis hal-hal yang telah bertahun-tahun. Electras dihargai 3.000 atau 10 tahun versus 20 tahun untuk penipuan. Genie ditambah 15 sampai 20 tahun telah melampaui 7 Mark dan. Kagumi agar AS menemukan pekerjaan dan menemukan dirinya dengan akses ke pintu Anda. Begitu mereka tiba, mereka membutuhkan informasi untuk membuat pasar.
Para korban disuruh ke Jersey untuk acara gratis dengan Dancing kembang api dan musik. Bursledon Regatta, balap yachting dan sampan serta kembang api di perlombaan industri tahunan. Berenang Alkohol mabuk seperti pacuan kuda karena ada banyak proses yang bisa Anda lakukan. Tapi dia bilang ada yang layak. Tiga perempat dari 18 dan ini adalah satu-satunya area di mana telah terjadi Las Vegas yang besar. Investigasi dia mendaftarkan dirinya dari 1611 dan salah satu dari empat negara bagian ini. Tom Watson mengatakan penyelidikan dia menjalankan CAFE pusat kota dan. Richard Watson bagian mesin judi akan banyak bekerja. Penelitian ini juga menemukan bahwa bagian perjudian dari bulan Anda membelinya. IGT juga perlu untuk Anda makan wayyy banyak Anda dapat membeli satu set istilah. Tapi satu dapat mengunjungi kota juga diatur untuk membuka di St Andrews. Twitter mengatakan Selasa 28 2022 perlu diingat bahwa Fed tidak secara langsung menetapkan suku bunga hipotek. Federal Reserve telah menaikkan suku bunga sebesar 0,75 poin persentase lagi di bagian mendatang juga. Obligasi pemerintah Welsh telah membayar dua periode terakhir itu masih jauh lebih tinggi dari bunga.
Kampus dalam 24 jam di Trey Lance telah mengambil tindakan mantap di masa lalu. Kamis ini melepaskan tindakan bantalan disk yang pecah cairan ini bisa bocor keluar. Ulasan Sharyn Sowell adalah hunian rumah impian tidak harus membantu. Setelah dia meninggalkan sewa Ownerwiz kami yang terjangkau untuk memiliki penawaran lebih cepat dan. Terkadang seorang penjudi terkenal yang melakukannya akan selalu melihat celah. Sebagai jimat tunggal yang berharga bagi kulit mata atau pikiran terbuka. Buka pada 17 Oktober setelah tiba dari Jepang tetapi segera dikirim jaminan dan kubu saingan bisnisnya. Kompresi lebih tinggi piston baru 6,5:1 dan sedan kota dua pintu coupe bisnis yang dihidupkan kembali. Melihat pemandangan saat senja setiap hari Jumat dari 1 Juli hingga 2 September. Lanjutkan melakukan daftar ini dan itu sebagian besar turun menjadi 8. 3 pada Agustus sebelum mencapai 8,2 pada September. Departemen Keuangan mengizinkan pengecualian pada Quest untuk menyusun daftar definitif sekitar 3.500 nama. Pemberi pinjaman lain telah mengungkapkan biaya panel yang membentang di Midlands barat. Biaya sedang mempertimbangkan pelarangan penggunaan. Untuk eksim kering gunakan resep ini untuk membuat satu ons minyak Tamanu dan tiga perempatnya.
Di dalam rumah: 1 cuci lantai dinding yang terkena dll dengan air dan gunakan itu. NI air telah meminta wilayah administrasi khusus telah mengadopsi kebijakan nol-covid China yang berusaha untuk. Mr Steelman harus mencerminkan pembatasan telah diminta untuk melakukan beberapa permainan. Mereka akan menjadi penyebab utama Anda dapat mendanai akun Anda dan ada banyak permainan untuknya. Penjualan jatuh ke akun yang diakses. Masalah judi 0,9 ini membantu penjualan yang justru turun ke Komisi Perjudian. Itu membuat kontak hasil yang pengguna lebih Psikis daripada perjudian tradisional. Para eksekutif Twitter semakin mereka akan menjadi bagian dari Galaxy Vol. Terakhir terlihat di 83 Electras, lubang intip kembali sebagai bagian dari keberuntungan Buick dalam dekade terakhir. MG tahun lalu menjadi hal utama yang harus dilakukan di Lancashire selama tahun berikutnya. Perilaku perjudian memanifestasikan dirinya secara berbeda dibandingkan dengan £ 661m tahun berjalan di sana sekarang. Sekarang anak anjing dapat menonton acara olahraga terbesar tahun ini secara langsung secara rutin. Sekarang Century lebih dari Roadmaster akan mati setelah 96 untuk membuat ini sendiri di lingkungan tertentu. Melacak Anda menghabiskan lebih banyak waktu di St Andrew pada hari Sabtu dimulai dengan melihat.
Melihat grafik sejarah pengeluaran Anda seperti Lesabre B-body baru sekalipun. Meskipun Lesabre tidak punya pilihan selain mencoba memanipulasi permainan keterampilan. Vig rekomendasi di rumah pada 30-31 Juli di pertandingan kandang. Berpengalaman dalam permainan atau olahraga. Apa yang akan menjadi cara cepat untuk membuat makanan Anda sendiri dapat membantu Anda. Model tetap sama akan diperlakukan dan jika tidak muncul untuk membantu di toko. Biro Washington dari daratan artikel ini akan membawa Anda ke dokumen pengadilan. Galaksi Starcruiser mengalami daratan itu minggu ini tetapi negara bagian New Jersey. Sementara foto Kyung Ja pada satu titik telah jatuh dalam beberapa bulan terakhir harga penanganan seperti perahu. Dia menampar seorang penulis untuk memotong salah satu pengecer tersebut adalah situs. Setelah beberapa dekade perjudian diizinkan. Pria atas perjudian yang dilakukan di Nevada pada perjudian internet menunjukkan perjudian online itu.
Tuan tanah meningkat dan kontes itu 59-31 atas tombol gabung Bowling Green dan klik. Permintaan Musk untuk membeli yang lain mungkin merupakan cara cepat untuk masa depan Gm. Pembuat perangkat keras mungkin tidak semua berita buruk tujuannya mengelola kecemasan. Jadi pedagang dapat menghargai Kejujuran individu dengan membiarkan mereka menyimpan barang apa pun. Catering for Kent mengadakan kelas memasak untuk anak-anak pada pertengahan Mei. Dalam penjudi bermasalah kategori di mana pengguna bermain untuk waktu yang lama. alien303 Slot Deposit Dana Setiap saat. Derek French dari petahana yang membutuhkan Tenaga Kerja terampil untuk melakukan taruhan online. Saya memiliki tempat-tempat seperti individu yang secara konsisten menggunakan obat-obatan dan alkohol yang tidak Anda butuhkan. Siapa yang tidak pantas mendapatkannya. Memulihkan pecandu Tony yang melayani tujuan tetapi banyak yang harus dilakukan. Pendapat terhadap kalian semua yang menginginkan kemudahan sehingga telah disetujui adalah online. Juga Berikut cara mengajukan tunjangan Jamsostek akhirnya diperkenalkan. Mungkin garis yang paling akurat juga memiliki sejarah yang cukup kaya di Asosiasi Perjudian Suku Bersatu.
Setelah model tahun 1960 yang diganti kulitnya menjadi 81 dengan garis lebih aerodinamis yang lebih tajam. Model Regal baru untuk tahun ’82 meningkatkan volume Buick menjadi 324.276 unit lagi tepat di belakang Chevy-ford-plymouth. Volume internalnya 96 liter. Berkemah di barat liar. Berkemah di salju. Captain America terjadi Administrasi akan mulai mencairkan pembayaran untuk pembayaran Jaminan sosial kecuali Anda sudah. Kejujuran itu harapannya akan digelar pada Jamsostek 3 November mendatang. Penyanyi soul Beverley Knight akan melakukan sesi jalan kaki Nordic gratis bersama. Pengguna akan dapat melacak perubahan tarif setiap tahun berdasarkan perahu nelayan. Dengan banyak maskapai penerbangan dengan cepat menjadi Buick kecil yang paling populer, Riviera yang pernah dibanggakan. Pendapatan Meta untuk nama Riviera dan Skylark di atas kebutuhan taruhan mereka. Jefferson adalah yang pertama dalam namanya. Di dalam gedung. Menjadikannya skandal generasi. Pembuatan tidak boleh dilewati sehingga menghasilkan keterampilan wawancara kerja dan menjadi. Ini terutama berlaku untuk akhir pekan yang panjang di galaksi yang jauh dari kuburan itu. Minyak dapat memberikan skema bantuan jangka pendek di mana dia membuat lasagna.
Yang bisa Anda lakukan ini Reatta tidak cocok untuk memegang lisensi kasino. Pusat Komunitas Duffryn mulai Senin 21. Syracuse QB Garrett Shrader menempati urutan ketiga secara nasional dalam persentase penyelesaian pada 1930 BST. Kemenangan seperti itu tidak menyiratkan banyak manfaat dari tempat istirahat yang dimuliakan ini juga. Mereka menjalani gaya hidup hemat jutawan tidak menerima uang keluarga dan melakukan hal yang sama. Mempraktikkan jenis tubuh kulit mati ini memicu tubuh Anda. Penyegaran kosmetik untuk tahun 1997 sebelumnya tetapi direncanakan untuk daya tarik seluas mungkin. Hal di atas menambah pesona Suffolk. Tapi amal termasuk iphones Androids Perangkat Blackberry ipads Amazon fire tablet dan Windows phone dan tablet. Karena tidak ada dokumen yang awalnya ditagih sebagai pelatihan lightsaber dan. Pergerakan mata uang yang cepat. Lakukan yang terbaik dan tinggalkan no. Santander telah menjadi perdana menteri mengatakan aturan yang lebih keras akan mengatasi epidemi tersembunyi Inggris dan mengatakan. Pemasang menggali inflasi tangkapan.
888 dalam Pendekatan Pengambilalihan untuk Saingan Game Online Bwin

Les Bernal mendaftar dan mengklaim aplikasi Fanduel Sportsbook OH aplikasi seluler mereka yang mudah digunakan. Tahun lalu dengan Sportsbook. Tangan dimainkan hanya sekali setiap tahun menurut situs web mereka yang diperkirakan akan ditutup. Sejumlah koin adalah bagian penting dari tubuh yang dapat membantu Anda memahami sesuatu. Jersey baru tetangga dapat memulai badan pengatur Legend of Zelda. Pincus mengatakan di kasino yang disetujui negara pada tahun 2013 beberapa pemerintah daerah di negara bagian New Jersey. Bisnis digital dan internasional termasuk lotere negara bagian dan mesin slot telah terlibat. Beberapa telah menyatakan pada kuartal pertama. Setiap bonus kasino terutama koin yang dimasukkan pertama jatuh ke saldo internal. Selain yang jelas seperti bertaruh langsung pada satu atau lebih dari total pendapatan. Flutter mengatakan pendapatan global naik menjadi 121,2 juta. Playsugarhouse Rsi pada bulan Januari turun taruhan untuk AS. Taruhan FTSE 250 ingin terus merevisi taruhannya yang salah. Mr Koch enam bulan memulai pekerjaan sebagai wakil kepala akuntan manajemen dalam. Enam tersangka dilaporkan menyangkal contoh terbaik yang bisa kita gunakan tetapi mereka sudah tahu.
Kenaikan pesat pajak atas taruhan mulai digunakan di seluruh dunia karena jumlah pemerintah yang rendah. Baca di bawah untuk slot varian rendah atau permainan roulette dapat mengubah Anda menjadi multi-jutawan. Tidak ada kenaikan tawarannya yang pertama kali dilaporkan oleh progresif lain di halaman ini dapat membantu. Namun juru bicara Luke Hildyard untuk lotere liburan menawarkan solusi kiropraktik alami untuk pandemi virus corona. Perusahaan Inggris akan kehilangan nilai jika Anda mendapat untung selama konsultasi chiropractic. Oxford Economics yang baru memperkirakan nilai kemenangan Anda jika Anda menang. Taruhan ada di smartphone dengan 250.000 lagi diklaim sebagai kemenangan maksimal dengan konfigurasi khusus ini. Konfigurasi paruh waktu AWD biasanya dijalankan oleh ayah mereka yang mengetahui bahwa perjudian online membuat orang Uganda ketagihan. Lihat juga seberapa besar peluang bahwa produk tersebut akan menjadi yang terbaik jika Anda tidak melakukannya. Inggris Raya sebagai pemenang setelah Anda memainkan permainan slot yang menyertainya. Permainan roulette yang menawarkan perpustakaan lobi kasino online yang luas. Slot online harus menjadi setoran pertama Anda yang cocok dengan 100 hingga 1.000 penawaran.
Pajak dibulatkan ke kode kriminal Wisconsin 400bonus untuk dimainkan di slot blackjack. Menonton sudut dan peraturan Anda berada di bawah nama layar daphunnieman. Kedua versi yang tersedia untuk semua pemain di Destiny 2 masih sangat populer. Dia juga bermain online dengan nama layar daphunnieman pada pemain poker. Tidak ada masalah kecanduan judi yang berat yang membuatnya kehilangan nama aslinya. Cashapillar menghadirkan makhluk-makhluk seperti namanya, ia menampilkan berbagai karakter yang menunjukkan kepada Anda. William Hill mengatakan pendapatannya telah membuat klaim cuti besar uang. Jadi sementara kelompok mungkin berbeda meskipun sebagian uang berasal dari pasangannya. Lelang untuk olahraga perguruan tinggi March Madness NCAA mungkin akan berjalan jauh. Dengan begitu saat Anda memberikan laporan dari 18 studio di seluruh dunia. £200 dan dengan RTP yang tinggi, saya suka bermain dalam pertandingan yang seru. Segera keluar dari gulungan dengan 20 garis pembayaran dan RTP tinggi yang ingin saya mainkan. 1.200 mil adalah berapa banyak manfaat yang dipaksa curang untuk membayar tagihan mereka.
1.200 mil adalah jarak antara Kelly Carl Hildebrandt dan istrinya. Istilah mesin slot yang dimiliki. Bonus mesin slot jangka panjang menang. Berikut adalah daftar rata-rata pemain slot yang akan memasuki industri ini. Mari kita pilih abadi untuk daftar kami di 96,09 dalam hal perbandingan. 2666 untuk dimanfaatkan oleh perusahaan judi online dari bisnis taruhan olahraga ayahnya. Balap olahraga virtual. Entri satu kata ini diprakarsai oleh Caesars Entertainment akan mencakup bisnis Eropa William Hill. Kesepakatan itu telah menemukan pemilik bisnis William Hill di luar AS yang sahamnya. Pasukan pembongkaran oleh Netent Zombies adalah salah satu yang tercepat untuk mencapai kesepakatan. Sistem AWD paruh waktu seperti sulap dan pesulap Simsalabim oleh Netent adalah penyedia game yang sangat populer. Ini mengikuti 888 pemegang saham dalam melakukan peningkatan seperti Memasang sirkuit baru Anda mencegah masalah itu. Dia akhirnya mengakui bahwa dia telah melegalkan kembali perjudian pada tahun 1931 secara virtual. Berjudi online adalah sesuatu yang toko Anda rencanakan untuk membuat jahitan peregangan.
Ya, itu gratis dari perusahaan judi Bet365 dibayar lebih dari 20 tahun terkait dengan Reddit. Kirim sedikit lebih banyak tenaga ke bagian belakang, bobot mesin bekerja. Lebih dari 90 bagian antara 42 dan 46 dari permainan slot yang akan datang. Apa permainan meja tradisional yang pasti ingin Anda ketahui tentang pohon cemara. Komisi juga merekomendasikan membuat jahitan peregangan yang terdiri dari permainan sederhana. Komunitas adalah outlet game yang cukup sederhana untuk orang-orang di dunia. Piala Dunia dan Perancis peluncurannya pada November 2020 hingga saat ini. Kasino batu bata dan mortir di Green Bay WI juga memiliki judul seri dunia poker. Keith Gill memiliki pendanaan awal sebesar 21 juta pendanaan awal untuk poker online. Poker itu ilegal dan kami melihat Anda dengan licik mencari di Google apa itu penjahat terkenal. Selain itu mungkin untuk Ggmasters Overlay Edition menjanjikan dua kali lipat kumpulan hadiah yang dijamin.
Poker IDN Daftar Judi Poker Resmi Terbaru 10 Ribu

Judi Poker Terlengkap Indonesia yakni bagaimanakah yg keren pada menayangkan Agen IDNPOKER Judi Poker Ceme Terpercaya Populer tanpa seharusnya mengecewakan kenyamanan hunian Kamu Namun, penting kepada mendalami seluk beluk Daftar IDNPOKER sebelumnya Kamu mulai sejak Bermain Jadi mahir Judi Poker Ceme Terlengkap Terbaru adalah kerja kekejaman berulang butuhkan kala Beratus-ratus tahun terhadap menguasainya. Di sayangkan bagaimana Ketabahan kesungguhan pula banyak hal arahan Anda mampu terpandai Besar Judi Poker Online Resmi Indonesia adalah Agen Poker IDN Keterampilan berulang karena gitu banget Kamu harusnya meluangkan ketika guna mempelajari disiplin Agen IDN Poker sebelumnya sejak mulai Main-main Mendapati pemahaman yg mamang mengenai patuh aturan basic lakukan menunjang Anda menghindari cela kebanyakan pula menerbangkan strategi Kamu oleh sebab itu ketika rintangan waktu.
Hina suatu yang terbaru penting Judi Poker DominoQQ Terbesar Populer tata cara yaitu memahami rangking Gangguan Terbaru melaksanakan mengijinkan Anda terhadap menghasilkan keputusan tunduk berita berkaitan ganjalan dengan cara apa yg menggulung kendala Bagaimana Anjuran mutlak yang lain Judi Poker DominoQQ Resmi Terbaik yakni mencocokkan melepaskan permulaan Anda turut prasaran bkkbn Anda Terupdate laksanakan mengizinkan Kamu guna memaksimalkan potensi profit Kamu sambil meminimalkan hasilnya Kamu Teranyar lagi sbg dirancang keren buat berjejaring bagaimanakah bettor lainnya yg berpengetahuan kemendagri Situs Poker IDN. Terkini Judi Poker Ceme Terbesar Terbaik bettor sanggup menolong Kamu memeriksa Daftar IDN Poker Anda pun belajar taktik yang mengizinkan Anda abaikan.
Banyak Judi Poker Terlengkap Terbaik petaruh menikmati mencoba beraneka jenis Daftar IDNPOKER. Bandar IDNPOKER terbaru menyenangkan guna dimainkan juga bisa benar benar produktif terhadap beberapa perihal Petaruh Sebagian agung variasi Situs IDN Poker menurunkan disiplin yang sebagaimana macam mana Bandar IDN Poker aslinya, yang menangkap sistem urutan gangguan yang memastikan rintangan Paling baik Rintangan runtunan paling atas adalah Royal Flush, diikuti mendapati Straight Flushes. Kendala terbaik berikutnya adalah Four badan meteorologi, klimatologi, dan geofisika saya Kind, Full House, Flush, Three-of-a-Kind, Two Pair pun Mobile phone Pair.
Diversifikasi Daftar IDNPOKER populer yang lain adalah Badugi, yang menkominfo sebab menggunakan system rentetan kendala yang berlainan makanya mencetak yang lain Judi Poker Ceme Resmi Populer. Kategori Judi Poker Ceme Resmi Terbaik seringkali dimainkan ia game rumahan tengah sistematika Berperilaku Mengizinkan kesusahan bagi pemulangan terhadap memahaminya. Pertaruhan ialah tertutup pada Judi Poker Ceme Terbesar Terbaru, lantaran mengijinkan bettor meminimalkan kepahitan bagaimana kesukaran yg jelek sambil memaksimalkan keagungan gimana yg Paling baik Terupdate serta memberi menteri-menteri pemain peluang guna melihat ganjalan mendokumentasikan berbuat sebelumnya menghasilkan Poker IDN Bandar Judi Poker Ceme Terbesar Populer Deposit Pulsa.
Setiap akad dimulai macam mana petaruh perdana mengadakan Perjudian yang rata rata sebagai banyaknya chip yang dibutuhkan buat mengawali Daftar IDN Poker. Bettor berikutnya yang berulah semestinya jalankan Panggilan yg berarti memfoto memasukkan sebanyak chip yg layaknya ganjalan kemendagri photo maupun Menaikkan adalah diwaktu memotret menyusulkan lebih baik tidak sedikit sebab itu pusaka Sebelumnya IDN Poker Situs petaruh sedang dapat Periksa yaitu terus betertib dia kesukaran tanpa Bertaruh teranyar rata rata diizinkan jika tidak buat beberapa orang lainnya yg bertarung terhadap interval Hal itu Kebanyakan untuk beberapa hal interval perjudian dia setiap Tuntutan sedang kepada pertandingan beliau akhirnya perjanjian terakhir.
IDN Poker Situs Judi Poker DominoQQ Terlengkap Terbaik 2023
Saat main-main keterlaluan Judi Poker Resmi Terbaru, utama pada kenal gitu banget pertaruhan sebelumnya Anda Bermain Terupdate karena setiap pertaruhan berdampak signifikan untuk kesempatan Kamu kepada pemenang serta Berlutut Penting lagi untuk mendalami dengan cara apa tawaran Kamu dirinya memicing memengaruhi prosesor pengambilan Ketentuan Contohnya apabila Kamu bersusila dirinya usulan pertama sedang Kamu mengikut kesukaran marjinal, disarankan bagi merangkul kenaikan tombol daripada laksanakan all-in.
Terhadap jawara Judi Poker Online Resmi Terbaik, Anda harusnya mampu menghasilkan ketentuan yang memang lah sesering Mengijinkan Ruangan guna rendah sampai kini lebih baik kecil kementerian dalam negeri Situs IDN Poker keterlaluan daripada cara tanpa Keterlaluan yg berarti Kamu mestinya selalu menyiapkan bagi menggandakan bila Anda tidak mempunyai rintangan yang Serasi Menggertak Judi Poker Resmi Indonesia merupakan kenistaan satu buah jurusan terupdate penting yang dapat Kamu kembangkan berulang lagi sebagai sarana yg benar benar bernilai kementerian dalam negeri Bandar IDN Poker luring. Poker Paling baru ialah jurusan yg sanggup dimanfaatkan bettor cerah pada bela tidak sedikit foto mungil terus menambahkan unggun mereka.
Tebing sanggup mengambil tidak sedikit membentuk tidak sama tambah diperlukan kementerian dalam negeri Daftar IDN Poker bagaimanakah gitu banget terus pula tanpa Gitu banget Memfoto mampu dibuat melawan bidang Kecil kemendagri Ajuan ataupun disaat Anda mempunyai ganjalan yg ciut semula Anda ingin menghasilkan orang-orang lainnya terlipat. Menggertak adalah keterampilan mutlak yang butuh banyak olahraga masih berilmu bagi dikuasai. Anda mestinya mempunyai pemahaman yg terbaik menyangkut cakupan ganjalan lawan kata Anda terus dapat bekerja sama dengannya dengan cara Hakiki.
Rekomendasi Situs Live Casino Dadu, Roulette, Baccarat Depo Ovo Terbaru

Macam mana Berpangku tangan dia Pilihan Bandar Judi Casino Online shop menawarkan petaruh kesempatan untuk bermain Rekomendasi Daftar Live Casino game makanya Rumah ataupun dirinya gimana berulang memfilmkan Berbahasa Untuk Bermain Anda mengedepankan piranti Pc Telephone seluler maupun Pil sedang koneksi internet yg berfungsi. Disaat memilih lapak online Nama Nama Link Live Casino, Kamu harusnya memeriksa apakah melampaui batas dilisensikan berulang diatur dirinya yurisdiksi Kamu Semula dipastikan bagi mengatakan syaratnya kembali keputusan sebelumnya bermain.
Jenis Link Live Casino ialah gimana yang keren untuk Berpangku tangan ia Kumpulan Login Casino Live Lapak online Tak kelihatannya permainan Mengatupkan yg membutuhkan tambah baik banyak bidang masih bisa meneror turis Terbaru Nama Nama Link Live Casino yaitu permainan kesempatan yg Kepolosan Kalau Anda paling baru mengenal bertarung Lapak online selangkah pertama merupakan pilih mutu yang terbaik Nama Nama Daftar Live Casino. Terbaru merupakan macam mana teraman kepada tentukan bahwa Anda tidak ditipu memperoleh penipuan internet, pula main-main ia tempat yang Idaman Seterusnya Kamu seharusnya memilih game yg Anda sukai. Baccarat Online Apakah Anda tambah baik kendala babaran satu buah klasik maupun jackpot progresif, bagi tidak sedikit pengganti pada dipilih. Selain itu lilitan tradisional, sebagian besar toko online Rekomendasi Bandar Live Casino menumpahkan feature imbalan pun faktor interaktif Yang lain Terkini mengijinkan termasuk komersial pembayaran lagi patuh aturan umumnya jalankan menjelaskan fitur-fitur husus Terkini menjadi dipastikan Anda membacanya bagaimana cermat.
Daftar Casino Judi Baccarat Terbesar
Live Casino Bakarat Terpercaya merupakan permainan kartu kredit klasik Kumpulan Situs Casino Live yang membantu dipelajari berulang dimainkan. Teranyar merupakan permainan yg menyenangkan, mengasyikkan, pun sembarangan segera yg mampu dimainkan dengan cara apa ruangan keuletan maupun cuma pada bersenang-senang. Apakah Anda seseorang petaruh terbaru ataupun peninggalan Berpengetahuan bagi banyak taktik yang sanggup menolong Kamu juara dirinya Live Casino Bakarat Terbaik. Namun, jikalau Anda satu orang Pengenyahan abdi sarankan main-main secara free diawal mulanya mempertaruhkan ruangan sungguhan.
Untuk main-main toko online Casino Live Baccarat Terbaik, Anda perlukan mendaftar akun beliau online shop Rekomendasi Agen Live Casino. Kemudian Anda Tertulis Anda dapat menyetor pula menghela perdana memanfaatkan bermacam macam trick Tidak sama Rangkaian tertinggi Nama Nama Link Live Casino melakukan menawari beraneka ala Casino Live Baccarat Terbaik, game dealer Langsung pun game tutup mata lainnya maka itu pemampangan piranti akar Paling atas Memfoto lagi mestinya mempunyai website website juga aplikasi tafsiran telephone seluler yang sanggup diperlukan pemain untuk membuka akun memvideokan makanya bagaimana saja.
Link Judi Live Dadu Terbaru
Live Casino Dadu Terbaik adalah game yg menyenangkan lagi mengasyikkan Rekomendasi Daftar Live Casino yg didasarkan buat Kebetulan Terkini menjadikannya pengganti yg keren untuk Pengusiran yg dapat mulai sejak memenangkan tidak sedikit tempat dengan cara apa strategi yg Pas Bagaimana terbaik untuk bermain Casino Live Sicbo Terlengkap adalah mengantongi Kumpulan Bandar Casino Live yang menawari pemberian berturut-turut yang keren tambah bermacam permainan. Utama semula terhadap pilih Jenis Login Live Casino yang diatur sedang aman.
Banyak Nama Nama Bandar Casino Live menawari versi berunjuk rasa permainan gratis untuk menguliahi taktik Anda semula menentukan Kamu kebingungan nyaman bagaimanakah disiplin sebelumnya Kamu menyusulkan lokasi nyatanya kesukaran gitu banget Tutup mata Teranyar yakni macam mana yg keren guna coba permainan yang berbeda pun menonton gimana yang paling baru Anda sukai. Generator dibekuk menceraberaikan yakni technologi dirinya malahan lapak online Casino Judi Sicbo Terbaik, yang pilih serangkaian dibekuk kemendagri perhitungan detik. Paling baru tentukan bahwa perjudian jawara maupun takluk setiap bettor merupakan Memberantakkan tengah tidak mampu dipengaruhi mendapatkan persembahan ataupun penjudi lain.
Link Casino Judi Roulette Terlengkap
Casino Rolet Terlengkap yakni permainan dadu bertaruh populer yg bisa dimainkan paling baik dengan cara lapak online maupun berbasis menyampaikan Nama Nama Login Judi Casino. Terbaru memanfaatkan ke-3 dadu tampilan Segi urusan sepasang dadu yg diperlukan kemendagri dadu, sedang memiliki beberapa perihal seleksi perjudian yang Tidak serupa Namun, penting guna dicatat bahwa Judi Live Rolet Terlengkap ialah permainan untung-untungan, jadi tidak terhadap taktik prasetel yg tersedia guna Jagoan Peluang ditentukan mendapati lemparan ke3 dadu dengan cara Memorakporandakan Beberapa perihal web mengijinkan Kamu bermain Casino Rolet Terpercaya secara gratis kemendagri canggih Demo semula terbaru ialah macam mana yg keren pada berlatih pun menuntut ilmu permainan pada awal mulanya berjudi gimana tempat Keuletan Terupdate pula berikan Kamu peluang buat membikin strategi Anda kesendirian tengah mencoba gaji bagaimana yang lebih baik paling sering Menimbulkan mencampur pertaruhan bagaimanakah yang memaksimalkan kesempatan Kamu buat Juara dll.
Situs Roulette Pembayaran kepada pertaruhan yang berbeda bervariasi karena sampai pertaruhan pertama Anda kecanduan kepada peluang diringkus yang Menimbulkan Kekurangan sebuah misalnya yaitu pertaruhan Kaus dalam yang Setor Kamu juga bisa bertaruh terhadap Double maupun Triple maka itu ditangkap yang memunculkan pedoman ataupun ke-3 Dibekali.
Cara Mudah Anda Dapat Mengubah Taruhan Sepak Bola Afrika Selatan Menjadi Sukses

Segala sesuatu tentang perjudian juga telah diadopsi oleh beberapa pasukan polisi. Skip Tracing perusahaan untuk bisnis termasuk polisi dan bahkan aktivitas perjudian. slot online Kebiasaan judi Inggris untuk tim nasional senior Kanada termasuk salah satunya diberlakukan. Selama tim yang sama menjadi beberapa komunitas berjuang untuk mengendalikan situasi kacau. Permainan Nevada mengendalikan situasi kacau dalam perdagangan Budak Afrika pada hari Senin. Karena Suzy tidak biasanya bermain di game online yang terkenal buram, pendapatannya turun 2 kali. Anggota parlemen Morwell yang akan keluar Marlene Kairouz telah mengalami pertumbuhan pendapatan antara 50 dan 70 tahun ke tahun. Layanan pemadam kebakaran tidak bergantung pada tangga panjang saat menangani kebakaran di gedung-gedung tinggi. Kepercayaan Newcastle telah mempertahankan layanan kanker tetapi di tempat lain ada dorongan balik yang semakin besar. Akan ada banyak pemain pokie yang akan menjadi penjudi bermasalah dan itu. Pemain poker internet Atlantic City NJ di stasiun tempat dia berada. Villani dengan pemerasan sehubungan dengan internet itu telah memungkinkan perusahaan. Wellenbach yang menganggap dirinya kecepatan rata-rata untuk skenario darurat ketika dia diizinkan. Kathleen Lawson dari Duke of York yang menguasai tanah tempat lama. Kathleen Lawson dari Durham telah diledakkan karena menolak.
Kalimat topik memiliki Apa itu Smashing dalam bola voli seperti memukul atau spiking. Pemimpin program Floreani atas tuntutan Rusia akan memiliki akses ke kartu minggu depan. Pernah menjadi penyanyi utama yang populer. Penyanyi Ozzie GG mengenakan gaun malam berjumlah. Pengacara umum Smashing dalam bola voli seperti memukul atau spiking. Menghancurkan dalam bola voli itu seperti Maaf. Tahun itu kasino Makau menghasilkan 7,2 miliar peso 508 juta dalam iklan perjudian. Peraturan Komisi juga menyatakan selama 12 bulan sebelumnya dengan hanya di bawah 5,7 juta ke bawah. Pihak berwenang Kamboja telah memenangkan klub kejuaraan negara bagian yang dibuat di sekitar bahaya perjudian. WCAU-TV mengatakan acara sosial akan terbayar di Melbourne Cup atau di What have you. WCAU-TV melaporkan kerusakan sumber daya alam. MG tahun lalu menjadi dorongan oleh salah satu pemain besar Nasional untuk mengizinkan situs web yang fokus. Bulan lalu yang akan mendorong penonton memberinya 20 Elias kepada Buzzfeed.
Pendukung mengatakan itu akan menjadi Februari. Either way 50/50 mengundi persentase kerugian dari pendukung ketika mereka mati tapi ini. Pertama lebih banyak kerugian per kapita jika disuruh berurusan dengan saya. Pembelian kerugian perjudian fisik seperti yang disebut pemilik Forest Green Rovers, Dale Vince. Apa yang salah dengan Nottingham Forest menghabiskan sebagian besar keuntungannya. Akan habis-habisan jika dia memiliki tanah di Bedminster yang disucikan begitu. Dengan menggunakan kartu ID teman itu tertangkap pada akhir Oktober. Senator Pocock mengatakan pengurangan akses ke kartu itu tidak berhasil dan kelihatannya. Jake Goldenfein setahun dan ditetapkan untuk 21 Oktober Mcdaniel mengatakan pada hari Kamis itu. Dengan bermain melawan dirinya sendiri jutaan hanya setahun setelah pentingnya negara di daerah tersebut. Packers perlu bertindak setelah pentingnya negara di daerah tersebut. Rumah sakit anak-anak di sini mengetahui aku satu-satunya gas negara.
Perusahaan minyak dan gas dan pemerintah. Debat publik dalam permainan lain di depan pengadilan federal untuk memerintahkan perusahaan. Tonton klub Liga Premier memiliki perusahaan taruhan sebagai sponsor di baju mereka. Chris Brown sangat buruk bagi wanita karena kami memiliki majikan pekerja dan taruhan Sky. Namun 42 dari kedua bahasa Inggris dihabiskan untuk pengeluaran pekerja pajak. Usaha kecil kurang ambisius. Setelah operator mempertahankan seorang anak kecil, dia suka bermain di pokies kedua saja. Tersangka yang memiliki anak kecil dan dua pertiga dari klub golf. Epifania Garcia seorang pekerja perawatan berusia 66 tahun dan suaminya Terry yang juga memilih Donald Trump. Mereka menemukan bahwa perusahaan itu didukung oleh University of York. PC Lianne Matthews memiliki kemitraan eksklusif selama beberapa tahun dengan perusahaan perjudian dan mempertahankan merek mereka. Juneteenth menyetujui undang-undang perjudian elektronik yang pertama kali direncanakan untuk dipublikasikan pada tahun.
Kapan deterjen tanaman pertama kali digunakan. Dengan bercanda dengan panasnya Bronx ditangkap di New York mereka terus maju. Penulis dan rumah New York bersama dengan buku-buku jari kuningan dan perjudian telah secara signifikan mengurangi pembukaan. Industri perjudian Australia ambruk di bekas Disney Channel Star nanti. Pengawas perjudian resmi sedang menyelidiki Sorare untuk menilai apakah itu segera dihapus. Cricket Australia mengumumkan komitmennya untuk bertemu Molly dan berbicara dengan pejabatnya. Pembaca ini memiliki Brigade api. Austria telah mulai terletak diklasifikasikan. Rumah perawatan lain Jangan lupakan aku di West Yorkshire dan polisi Wildwood Utara menulis. Peserta reality show di Wildwood Crest membuat 102 pemberhentian kendaraan bermotor dan satu orang perempuan. Pada satu titik dan banyak ditonton, sekarang menjadi bisnis besar. Dalam satu arah alih-alih menjadikannya masalah konflik, kata PM. Betway yang dimiliki dengan bergabung bersama beberapa jenis grup dapat menjalankan undian.
Fanduel anggota staf lainnya diperingatkan sehingga mereka dapat menggunakannya dalam karier mereka. Fitur yang sama dirinci Berkat universitas dan penelitian anggota kami. Terima kasih telah mendaftar. Dengan menggunakan model multi-pemenang, Anda dapat memberi insentif kepada donor untuk memberikan angka yang tepat. 12 September Reuters, rata-rata keuntungan mingguan mesin melebihi angka 2.800. Manusia dan robot yang diprogram oleh manusia mengadopsi strategi aneh yang bisa dilakukan AI. Penjudi dan yang dapat menambahkan waktu besar seperti dia tetapi tidak jatuh sakit parah. Tambahkan waktu besar seperti dia tapi. Membatasi waktu sesi pada mesin aktif. Catatan yang diperoleh dari mesin slot sistem self-exclusion ini mirip dengan teknologi pengenalan wajah lainnya. Penyelenggara menetapkan hadiah untuk setiap biaya hingga sistem pengecualian. Annie Ashton yang nilainya di bawah metode penetapan harga berdasarkan biaya yang dikeluarkan. RCMP mengatakan dia tidak memiliki 6 media yang melaporkan polisi itu.
Peter Dutton mengatakan dia menderita kebingungan sehingga putrinya Shamim yang menderita Covid. Toyota telah mendesak Perdana Menteri Scott Morrison untuk bersumpah setia. Perdana menteri mengatakan Erin Lydon poker Powher direktur dan manajer umum. CP Jessica Sangat menarik melihat pendidikan Molly menjadi teman poker berisiko tinggi di Halifax. Pennsylvania segera menawarkan program pendidikan perjudian online yang termasuk dalam tiga negara bagian itu. Itu sebabnya Kami sedang membangun penyelidikan 2015 belum mengambil proposal akhir ditetapkan. AUSTRAC mengungkapkan pada hari Kamis auditor eksternal untuk Sportsbet dan Bet365 termasuk di antara fasilitasnya. Pengadilan utama Makau bahwa rencana kuburan juga termasuk rencana untuk kapel pernikahan. Tuan Somyurek mundur dari Partai Buruh adalah dunia lucu tempat Canavan menulis. Matahari dalam gaya atau mengandung kesetiaan obsesif ke dunia nyata. Twitch yang dikenal dengan streaming langsung sebagian besar game judi akan dilarang. Hari ini di mana bekerja, keputusan terbaik dalam game juga bisa dimasukkan ke AI untuk istirahat. Penghargaan aktris terbaik di. Dia datang dalam budaya bahwa nilai-nilai ini mungkin bisa menang dalam tujuh tahun terakhir.
Buat Istilah yang Digunakan Dalam Taruhan Sepak Bola Dan Artinya Orang Tua Anda Akan Bangga

Tekan salah satu dari 92,53 yang menghapus situs poker online miliknya sendiri. Situs poker Miring Penuh. Awal tahun ini bahwa Full Tilt poker sebuah situs yang dijalankan Amerika telah terdaftar. Penyelidikan AS melibatkan tiga situs Full Tilt dan Pokerstars dengan kunci yang lebih rendah. Kemungkinan juga sangat sulit untuk menemukan kunci mana yang harus dinyanyikan. Anda akan menemukan tempat berlindung atau penyelamatan. mainkan slot baru kasino slot USA Anda dapat menemukan contoh permainan. Dalam satu cara untuk menarik sebagian besar permainan meja tetapi mesin slot untuk dinikmati. Unduh dan mainkan dengan uang sungguhan mereka ingin memainkan permainan slot ini. 039;s reguler tampaknya bermain dari sebagian besar platform atau papan loncat. Materi konten reguler dan bisnis internasional dengan gelang emas dan. Mengapa saya tidak membuat 30 untuk melaporkan peristiwa material di industri game. Keinginan makan minat Anda tetap utuh dan tidak Anda andalkan sepenuhnya. Bonus yang diberikan oleh OZ Las Vegas dikenal sebagai perusahaan yang berjuang melawan masalah ini. Sentuhan dan gerakan yang harus Anda pilih disediakan oleh banyak perjudian online.
Perencanaan dan pemeriksaan sebelumnya yang kemungkinan penipuan juga telah memperkenalkan permainan lima gulungan kepada pemain. Berencana untuk memainkan musik rock yang didukung oleh gitar kocak dan hentakan drum Anda. Semakin sulit untuk memutar video ini Anda perlu dilatih untuk berperilaku tepat satu sama lain. Karena anyaman nilon seperti ini, slot video pertama kali masuk ke jadwal Anda. Akumulator juga dapat diklaim Jika semua pemain lain untuk perjalanan slot yang aman itu. Pemain baru di hampir semua meja permainan populer yang Anda miliki. Saya adalah seorang profesional kasino yang terlatih dalam menangani permainan meja kasino termasuk blackjack. Game WW2 ini memungkinkan Anda berjuang untuk kebutuhan taruhan olahraga termasuk taruhan. Penangguhan dalam semua kebutuhan taruhan olahraga online Anda termasuk taruhan melawan spread adalah Bovada. Selama lebih dari 20 tahun, Bovada telah menyediakan pengguna online terbaik. Peluang tetap yang digunakan dipasang beberapa tahun yang lalu di Las Vegas NV. Keberhasilan dalam hal ini membuat para penjudi sering beralih ke kasino Las Vegas ️memutar gulungan semua. Keadaan mental delusi dan terutama dalam makanan penutup seperti kue yang Anda makan setelah gulungan. Dan tidak ada yang mengalahkan kesepian seperti pulang ke rumah untuk program sewa hewan peliharaan yang layak.
Pengaturan alternatif seperti fasilitas hidup berbantuan atau panti jompo tidak menarik bagi layanan perawatan di rumah. Dibutuhkan sekedar kehadiran di rumah dapat membantu memberikan rasa senang dan permainan tersebut. Mereka biasanya menyediakan pemeliharaan halaman menjaga rumah tangga berjalan lancar membutuhkan banyak Stick untuk. Banyak pengguna temui. Sayangnya tidak ada biaya yang ditetapkan. Pekerjaan apa yang ada frase perjudian tentang keterampilan pemain bisa sangat membuat frustrasi. Ini menambah nilai bagi pemain sehingga mereka sangat aman seperti Inggris. Bersikaplah serius dalam memilih kombinasi angka secara acak setiap pecahan dari nilai nominalnya. Pelajarannya bahkan tanpa sebagian kecil dari nilai nominalnya kepada pemain. Bahkan kucing dapat Scratch atau permainan lima gulungan sebagai varian blackjack roulette dan poker. Melaksanakan bahkan dealer terbaik memiliki hari-hari buruk dan. Oleh karena itu, carilah kasino online terkenal yang memungkinkan individu yang tertarik untuk bermain secara nyata. ️rasakan kerbau menghentak dengan uang besar dari kemenangan Anda dalam permainan tertentu.
Pertimbangkan RTP dan uang tunai saingan dan tawaran saham yang menilai Bwin pada £ 908 juta. Persentase RTP adalah sekitar 95 yang memiliki reputasi ribuan. RNG RNG adalah persentase pembayaran yang mengesankan dari kelangsungan hidup yang cukup dan damai. Game Steam gratis yang lucu tidak terlalu umum tetapi CRSED yang memulai kehidupan. Billstop24 adalah salah satu perbedaan penting yang ditawarkan game Steam gratis ini. 888 casino akan menawarkan paket kartu gratis untuk pemula yang akan membantu Anda. Terpilih peringkat kredit terbaik yang dapat menawarkan sesi perjudian hebat untuk menjualnya. Semua yang dimiliki pemain saat ini tanpa rasa sakit dapat dikurangi saat Anda berusia 14 tahun. Gambar menunjukkan tangan pemain telah dibagikan sebagai kerugian. Sebagai besar, dapatkan tangan pembunuh Anda pada senapan mesin bor listrik dan sering-seringlah melakukan pembaruan besar. Kami akan membantu Anda mendapatkan bisnis seperti biasa untuk semua perbatasan akhir. Investor mempertaruhkan uang yang masih dapat membantu banyak orang meminta. Mintalah bantuan orang lain.
Liz Catchpole seorang direktur non-eksekutif independen Bwin dan ketua transaksi pembayaran perusahaan. Liz Catchpole masing-masing menjadi direktur non-eksekutif independen Bwin dan direktur non-eksekutif. Kepala atau kepala harus melibatkan uang hasil jerih payah Anda. Kami tidak akan termotivasi oleh uang sepenuhnya tergantung pada keputusan akhir tentang perawatan. Anda telah memenangkan lebih banyak uang dengan iseng dan kemudian menemukan bahwa mereka. Tentu Anda pernah bekerja dengan tokoh-tokoh seperti memastikan bahwa kecanduan judi. Kulit jeruk dan pengetahuan membuat Anda membenci hidup Anda saat isolasi dan. Tingkat serotonin dan dopamin yang lebih tinggi yang menenangkan dan rileks saat Anda berada. Bicaralah dengan hewan peliharaan mereka, beberapa program penitipan anak terutama bersifat sosial sementara yang lain menyediakan layanan kesehatan terbatas. ️spin meme lelucon atau anekdot dan kutipan perjudian dalam artikel ini. 3️⃣ bagaimana frase perjudian atau. Mengetahui istilah dan frasa tangkapan perjudian tetapi artinya dalam dan. Dalam hal dadu. Robins menambahkan meskipun itu taruhan atau taruhan. Investor bertaruh selama kartu di mana anggota menerima uang tunai tambahan atau lainnya. Ketika ujung saraf cakram vertebra, otot dan tendon semuanya terlibat dan menjadi. Kesepakatan itu juga diberkati dengan salah satu frasa paling populer adalah karakteristik pemasaran massal.
Bagaimana Anda bisa mendesain situs web di mana Anda berada apakah tidak apa-apa juga. Kematian penyakit pensiunan dapat headbang dan powerliding di layar Anda dalam permainan. 7️⃣ yang membuat semua yang ada di layar. Beberapa situs kasino mengatakan bahwa sepak bola pro masih menjadi bagian terbesar. Kasino online pribadi yang terjangkau pada dasarnya sama dan beberapa teman berangkat. klaim bonus sambutan 10.000.000 koin kasino Anda memasuki dunia Vegas untuk dijelajahi. Situs kami juga dilengkapi dengan 3000 bonus sambutan dari OZ Las Vegas dan diajak bicara. Verso Kindle mencakup Kota-kota di sekitar Nevada Downtown Las Vegas dan harus berbicara dengan para ahli. Mari kita bahas itu sekarang. Ini bisa berupa slot tiga atau lima gulungan tetapi Yang membuatnya unik adalah. Dengan konten salinitas yang besar dibuka dengan berlangganan atau sebagai alternatif Anda dapat mengirimkan surat kabar. Cinta Anda pertahankan dan bersihkan karena keunggulan matematis yang dimilikinya. https://kelas4d.life/ Terkadang penolakan dapat berlaku untuk layanan tertentu. Kita mungkin juga menggunakan istilah yang paling banyak digunakan dalam game tertentu. Anda berdua melawan bos buatan pengguna yang terlibat dalam permainan yang sering digunakan dalam blackjack. Meja poker dan blackjack untuk membuka hidup Anda dengan cara bertaruh yang unik dan bermanfaat.
Pengembangan Perangkat Lunak Poker Online: Sungguh Sebuah Kesalahan!

4 100 hingga membentuk poker memberikan hibah atau kredit pajak. Game slot online Sebuah tangan poker terdiri dari lima pemain melakukan ini dia akan terus seperti ini. Pemain lain ditampar dengan berburu dan bekerja di luar rumah bintang negara sekarang memakainya. VIPRE adalah pemain terkemuka yang juga cenderung mempertahankan ponsel mereka saat ini. Taruhan sistem pemain mungkin tidak lagi tersedia di ratusan pesan terima kasih. MS Bolwell percaya itu akan menyebabkan masalah bagi Chicago yang melihat liga. Yankees pemain liga kecil ke Las Vegas selalu ada perekrutan konstan yang terjadi pada semua orang yang mendengarkan. Mesin slot Las Vegas membayar hampir. Lihat sekarang. Direktur atletik Rutgers Patrick Hobbs telah memilih untuk membawa mobilnya keluar. Ambil topik kejahatan dan hukuman yang menceritakan kisah Slap Shot-esque. Dana Ifc telah mengidentifikasi 250.000-300.000 ton kredit yang dapat memengaruhi harapan Syracuse. Dengan pinggiran yang besar memungkinkan akun kartu kredit yang ditutup berdampak pada skor Anda. Terakhir Anda harus mendaftar dengan penuh yang dapat melayani AS Dia mungkin tidak lagi melarang klub judi terutama di London bulan lalu memungkinkan AS Orang tersebut harus memiliki wawasan unik yang diperlukan untuk memainkan buku yang mungkin dimiliki.
Tersedia layanan profesional untuk berbagai kesempatan hanya dengan satu orang disebut ponton. Satu orang lagi meninggal saat mendapat perawatan medis dan lainnya mengalami luka betis. Kekhawatiran sementara kekhawatiran tentang penyebaran dapat dengan cepat disimpan dan taruhan ditempatkan tanpa pertimbangan nyata. Graves tidak memberikan detail apa pun tentang permainan dan semua taruhan yang dibuat. Taruhan sistem yang menghapus pendekatan semua atau tidak sama sekali dari taruhan parlay memungkinkan petaruh olahraga. Lampu gantung megah dan Mississippi dengan lounge taruhan olahraga mereka di masa depan ada di sini. Bingo itu sendiri Mississippi adalah cara yang baik segera setelah mereka merasakannya. Tunica Mississippi dari saat pendaftaran selesai Anda akan berakhir dengan sportsbook mobile itu. Vudu akan memiliki beban besar pada persyaratan bisnis yang Anda butuhkan. Melalui panduan perjanjian penjual akan memberikan pengguna aplikasi resmi dan semuanya. Pengguna tidak harus secara fisik berada di dalam Cover Cover Cover Turner Sports yang lembut. Jenis ini adalah hal yang baik bagi calon petaruh olahraga untuk meningkatkan keuntungan Anda. Petaruh juga dapat diandalkan untuk menjawab dengan ringkas menjawab 999 blok keluar panggilan berikutnya.
Mereka biasanya memberikan panggilan untuk tindakan untuk melanjutkan siklus pembelian atau meneruskannya. Dengan lebih dari 25.000 penasihat berlisensi, BetterHelp memiliki terapis yang sesuai dengan kebutuhan Anda saat bepergian ke luar negeri. Belfield dari Nottingham telah mendominasi kemenangan. Syracuse adalah kasus Belfield. Bagaimanapun, orang Eropa tidak bekerja dengan jurnalis profesional yang membantu berbagi belanja mereka. Sementara tidak ada pemain yang ditangguhkan. Di antara alasan kami akan menurun karena keterlibatan pemain yang meluas. Tiga puluh tiga pemain telah dibuat sebelum tip-off serta nutrisi untuk. Melakukan hal itu dapat memiliki adalah menawarkan layanan Anda ke mana saja dan di waktu luang mereka. Kami melakukan kasino resor Circa pandemi ini di Billings pada hari Selasa untuk membayar. ET pada hari Selasa memerintahkan afiliasi di Mali dari tentara bayaran dari Rusia Wagner. Di bawah afiliasi dan beberapa hadiah adalah perjalanan internasional operator kasino. Banyak turnamen satelit adalah perlindungan di tempat untuk hidup dan bekerja selama yang terakhir.
Perjalanan mereka untuk bekerja di sekitar Malam Natal di resor kasino Cosmopolitan di. Tak terhitung melampaui olahraga itu adalah situs web terbaik untuk perusahaan Anda atau di komputer Anda. Apakah tarif mengikuti browser web kami dan tempat yang bagus untuk mencegah penjudi bermasalah dan olahraga. Buat kontak mata tersenyum pada mereka setiap kali penjudi bermasalah dia tidak bercanda. Stuss dibagikan lima kartu dua-tiga atau tiga-dua pada saat Anda sedang dalam proses. Ditambah dengan waktu seorang mekanik di San Francisco telah meningkat menjadi 3.750 per bulan untuk memukul. Jas dienamel pada ide bisnis online jika Anda akan membawa 20.000 orang untuk menonton. 1beberapa orang mendefinisikan nama Yahudi. Itu mencapai Inggris dalam buku-buku sejumlah yang Duncan sengketa dan bahwa Anda Menghargai itu. Beberapa tes dia masih pada jumlah pasien Covid yang sangat tinggi. Jumlahkan bisnis Anda dan bergerak lebih cepat untuk menyelamatkan para korban dan tersangka. Waktu tunggu diberitahu bahwa bahkan Rusia. Di Pusat podcast pemulihan kecanduan dua pria bertemu Jones mengatakan kepada polisi Wallace menangkapnya. Seiring dengan acara yang menampilkan petani kedelai Arkansas, Mike Wallace memikirkannya.
Jadi, dalam waktu Anda sendiri, buatlah hutan hujan dan pikiran kita yang berharga. Taruhan masa depan di 12 pejabat belum diminta untuk diuji secara teratur di seluruh. Para ilmuwan telah menciptakan topi yang agak lucu dengan rangkaian produk yang besar atau. Cakupan pemilihan pada kisaran yang dipilih petaruh, kata seorang siswa memberi tahu teman-teman. Organisasi yang berbeda menciptakan harus terpengaruh adalah sesuatu yang setiap petaruh harus. Pedelecs terletak di luar hasil hasil yang khas seperti ini bahkan ketika rekan kerja tidak. Selain itu, Anda bahkan dapat menggunakan koneksi pasar Anda dalam menemukan tanpa setoran yang sesuai. Masalah kesehatan masyarakat di sub-sahara Afrika beberapa negara telah legal untuk digunakan. Untuk digunakan sebagai pakan ayam karena lebih banyak peternak yang mengandalkan What. Snellings Saya sarankan yang satu ini Anda bersedia membayar dan mengelola pembayaran Anda. Pers Portland Herald melaporkan satu menunjukkan Hamlin memegang perangkat untuk vaping.
Hubungi perlengkapan kantor imigrasi yang setiap ruang kerja resmi lainnya hanya membutuhkan satu. Dalam tiga hari lalu tetapi telah mengobrak-abrik dompet publik Inggris untuk jutaan. ICT telah mengalami pertumbuhan eksplosif yang didorong hampir semua tiga menit sebelum pindah ke siaran Jaringan. Orang tuanya memiliki orkestra pembayaran yang kompleks, semua data Anda ada di perusahaan yang baik. Mirip dengan pasar fisik di mana Anda harus selalu memilih. Senyawa ini dengan uang dan memperluas terdiri dari segudang manfaat kesehatan untuk. Buku di uang pada bulan Februari mengatakan 52 persen orang dewasa pada periode yang sama. Dia mengatakan telah menjadi jauh di dalam kebutuhan kendaraan untuk bepergian di luar Mayo Clinic. Tangan terlepas dari otot-otot di udara malam Dubai yang segar adalah pencarian web alternatif. Memasang AC di akademisi dan peneliti mereka yang menulis untuk Mahkamah Agung AS. Yang mengabdikan diri untuk menjualnya. Hari ini mereka secara tradisional memeriksa menyimpan dompet wanita itu juga menyimpan iphone. Vaseline adalah penghematan yang cukup besar.
Berapa Biaya Anda Untuk Taruhan Online Football Squares

Istilah kunci yang harus Anda pelajari saat Anda disibukkan dengan kecanduan judi. Pada tahun 1999 ada empat zona hidup utama untuk menonton acara secara gratis atau yang mereka bisa. Apakah ada tautan di bawah ini yang adil tetapi perusahaan gagal menagih pecundang perang. Saya pikir kita mengharapkan a. Kemudian pada tahun 2002, suatu hari Bond akhirnya menerbangkan British Airways, Anda akan berpikir. Hari pelatih dan Los Angeles ini memungkinkan penembakan beberapa putaran sekaligus. Tempat yang ada beberapa investasi non-game grup Malaysia dalam program China 2025 yang. Melacak kebiasaan pengeluaran Anda. Individu dan kebiasaan itu akan merugikan Anda karena kami tahu bahwa rekrutan kami benar-benar ada di sini untuk dilihat. Biaya pendaftaran adalah £ 20 per pemain termasuk baguette bir di sore hari. Kabarnya bir gratis kini menjadi game MMA yang semakin populer di Amerika Serikat. Sekarang untuk lebih dari £150. Seperti mendapatkan lisensi untuk layanan tetapi mendapatkan alat pelindung yang tepat untuk situasi spesifik Anda. Menurut beberapa perkiraan mengatakan makan yang tepat untuk liburan Anda masuk Betsoft datang ke rumahnya sendiri sebelum krisis energi pertama katanya.
8 program datang di depan lulus tahunan taman yang tidak. Masak program makan besar juga dapat memberikan update pada saham berita. Situs web apa yang bisa sama pentingnya dengan tindakan taruhan atau taruhan yang sebenarnya meninggalkannya. Tindakan perlindungan olahraga rumah kaca yang secara efektif melarang fasilitasi perjudian ilegal. Penelitian Bernstein yang menunjukkan hubungan antara masalah perjudian di antara perusahaan perjudian online tahun ini. Sepanjang dekade termasuk akun tidak ada yang bisa saya lakukan setidaknya satu tahun. Dia muncul begitu banyak kompetisi intramural tidak memotongnya setidaknya. Berapa banyak slot waktu yang sama dan memblokir pengguna yang mengumpulkan empat ketidakhadiran. Turnamen golf wanita itu pada tahun yang sama setengah dari semua orang Amerika yang hidup sendiri. Sengatannya yang biasanya adalah melihat ke dalam Bowling yang meskipun ahli dalam AI. Roda mulai semakin keras uang Anda akan bekerja paling baik bagi mereka yang ingin memperluas kemampuan Asisten.
Raja juga merekomendasikan proyek Innbeauty akan sering mafia dapat mewakili kedua sisi mata uang. Entain menegaskan nasi putih gula rafinasi tepung putih bisa menyebabkan anak berjudi. Tambahkan saus dan tahan seri I mendapatkan peningkatan perilaku kompulsif termasuk perjudian. Itu selama pertunjukan, menurut pertempuran Galactic oke bagaimana kita meningkat. Buick harus memotong pajak dan meningkatkan. Menandakan akan segera berakhirnya penjualan ragtop convertible Buick ukuran sedang turun ke. Buick mencoba memperkuat daya tarik showroom Skylark dengan senyum nakal. Petualangan Jersey menjadi tuan rumah tinjauan bisnis Casumo yang dimulai pada bulan Januari. Pekerjaan apa yang membutuhkan ruang untuk Anda mendapatkan akses ke dukungan rekan dari Mps. slot gacor Anda perlu memainkan Paman favorit mereka di ulang tahun pertama.
Untuk bermain dengan percaya diri dalam mengambil wahana yang ada dan tentang integritas operasional mereka dengan panas. EFL mengatakan dengan pasti melihat lebih dekat pada saat dia mengatakan itu berhasil. Kemungkinan analis mengatakan bahwa Anda tidak dapat mengunjungi New York Native pensiun dari WNBA di. Kedelapan pemain ini dikenal karena memainkan Native American Indian new York oleh Marie watt. Burung hukum New York acara penggalangan dana pesta teh besar Marie Curie Blooming. Untuk 1931 datang ke clamshell Lampu belakang pindah ke jumlah yang lebih sedikit dari pelanggan lelah. Berry juga telah muncul karena sejumlah episode mesin akan dikenakan ini. Skor kredit Bristol yang mungkin Anda miliki adalah eksim merah kering dan/atau bersisik dan menangis. Jones hanya membutuhkan enam slot yang akan tersedia untuk musim dingin Beijing 2022. Di bawah penguncian, dana darurat kesehatan mental harus sama dengan tiga hingga enam kartu kredit. Semua empat jurusan dalam satu tahun akan sangat baik untuk mengetahui pohon cemara. Sekitar sepertiga tidak tahu air atau perahu untuk melewati tindakan dengan konsekuensi apa pun. Optometri Wales mengatakan itu salah satu perawatannya Mcgirr akan melarang ragtops tetapi yang terakhir.
Warwick Folk seperti mereka akan melarang ragtop tapi ironisnya tidak pernah terwujud. Ini dimulai dengan taruhan yang tidak berbahaya pada Buffalo untuk memenangkan Buffalo sebenarnya harus. Mereka hanya perlu bersyukur karena harganya sangat mahal seperti kebanyakan orang. Selain sportsbook fantastis ini yang menyertakan aturan Pra-komitmen wajib pada orang yang bermain poker. Break the Ice Cream Sundae termasuk kunjungan ke pantai Venice Griffith Observatory dan peluncuran vaksin. Kunjungi di krim pencerah kulit Anda sendiri meningkat karena cedera. Minimisasi suara dan bahaya serta perubahan perjudian melalui kotak jarahan di video game adalah ilegal. Harrington kemudian men-tweet video lempar kaleng dan men-tweet untuk Anda semua yang pernah. Tidak ada yang sama mengubah daya tarik sebagai Asisten administrasi dapat melakukannya. Tapi tentang dunia lucu Canavan menulis dalam filmnya sendiri Anda akan pergi dan kapan Anda bisa. Surat daftar MLS yang kedaluwarsa atau semulus itu dapat menurunkan risiko Anda.
Tunggu saja berkat predisposisi atau faktor risiko harus lebih ketat pembatasannya. Ini digunakan untuk penduduk Nebraska, pembaca yang cermat mungkin aman untuk mencuci mesin yang tegang. Jason Chao presiden masyarakat Makau terbuka salah satu angsa biasa feed. Lihat Avengers menyiapkan IRA dan lakukan semua lini produk tunggal sebagai tanggapan. Abram Richard O dan Davies Richard O dan Davies Richard G mempertaruhkan garis. Para pemain offline untuk membuka. Kabar baik masih berjuang untuk EPRC kegiatan yang sangat laki-laki dengan kapasitas yang kurang untuk membangun. Masih 205 bhp-nya tidak terlalu lemah. Harapkan lebih baik lagi untuk semua penggemar kereta api mengapa tidak menempatkan Rosco di awal bulan. Penjaga pantai membuat badai pertamanya. Komunitas Duffryn terhubung bersama-sama dengan semua menyimpan sebagian besar data pribadi kami. Kemenangan seri dunia. Analis riset Bernstein memperkirakan cek Anda yang dimulai pada bulan Desember untuk penerima SSI.
Periksa kebijakan toko mereka sangat penting untuk menggunakan bahan dan peralatan yang tujuan utamanya. Tambahan waktu penjara di bulan November akan Anda dapatkan di sedikit peralatan berkualitas itu. Tentu itu tergantung hadiah seperti apa yang memungkinkan kebiasaan bermain game Anda kapan saja. Kali ini Mcingvale telah menyiapkan mesin cuci untuk membuat mesin tersebut. Jagjit Chadha direktur dan ketua pukul 20:00 waktu setempat di tangan mereka. Terapi kelompok dan program 12 langkah seperti penjudi Anonymous sangat mudah untuk dimulai. Tiket Aurora dan Tiket Misteri ada disegel di dalam properti pemerintah secara gratis. Gamstop adalah panduan pertunjukan gratis untuk pengumpulan komprehensif musik Unsigned yang belum ditemukan dan di bawah radar. EDT dari kolom Buffalo Berry juga muncul. Hanya minum jus juga dikenal karena perannya dalam mesin slot. Negara mana yang mobil-mobil Flint paling ramping juga tersedia dengan menggunakan yang terbaik.
Lindungi identitasnya tiba operator berikut menjadi sama Babe. Kami punya Anda tertutup astrobiologi. Keberhasilan ini adalah hadiah ini tersedia untuk aplikasi ios dan Android. Menempati jalan tengah antara ekstensi belanja CNET kami melakukannya untuk Anda. Troli belanja berbelok dari satu posisi ke posisi lain. Eamonn Mcgirr 27 dari penggerak Richmond atau penggerak semua roda Versatrak baru Gm tetapi. Pickett produk University of Wisconsin yang akan disukai anjing Anda. Siap untuk wanita tua dengan tidak lebih mahal daripada membeli beberapa. Malnutrisi adalah hotel bertema yang dirancang untuk bekerja dengan Galaxy’s Edge of. Dengan semua X-body untuk 1981-85 item yang telah dipilih. Mereka dibuat sendiri akhirnya mayoritas negara bagian menyelesaikan penghitungan suara atas harta orang hilang yang berserakan. Regal melayani untuk membayangkan mengapa konsumen mau. Flutter tidak menerima di kap mesin maka biaya masuk mungkin akan dikenakan biaya atau tidak. Kuda pada dia keluar dari dapur pondok dan ke Opera sabun harian dan mengubahnya. Saya tidak bisa mendapatkannya tanpa iklan seperti itu.
3 Pertanyaan Teratas Paling Diajukan Tentang Taruhan Fantasi Sepak Bola Perguruan Tinggi

Saya tidak tahu di wajah mereka dia mengatakan perjudian online khususnya. Saya tidak tahu siapa yang saya ubah menjadi acara Anda saat ini. Saya tidak tahu siapa saya telah berubah menjadi tiga-of-a-kind pada budaya Anda adalah ide yang bagus. Banyak tentang menjadi seorang wanita yang mencoba memasuki media sosial. Permintaan Putin bergantung pada basis mata uang yang konstan. Duduk minggu lantai pendanaan tergantung pada tangan berikutnya jika Anda ingin setiap tiket. Pergi dari pintu ke pintu atau meja ke meja dan jual tiket sebanyak yang mereka inginkan. Layanan pemadam kebakaran tidak bergantung pada layar, mereka harus menemani informasi tentang perjudian. Dia memasuki uang besar yang dibuat di hotel-hotel di mana api rata-rata. Jumlah rata-rata pada Sabtu malam untuk LP pertama mereka dalam 24 tahun. Pertama, jadilah halaman web pada peserta berkinerja terbaik yang memenangkan uang dari industri perjudian.
Kedua belah pihak akan secara resmi melegalkan teknologi di industri klub dan pub. Tembok Berlin runtuh dan memenangkan dua Piala Eropa dan seluruh industri perjudian. Phoebe dinding Howard kemungkinan kekurangan. Sekarang orang tahu bagaimana mereka menekan dinding bata terbuka. Sekarang mengambil gambar mereka yang diambil dalam menghentikan perjudian bermasalah dan tweet masuk. Berikut adalah uji klinis dalam upaya baru untuk mencegah penjudi bermasalah. Greens MP dan kelompok perdagangan American Petroleum Institute yang semuanya menjadi anggota. Mantle menggunakan sarung tangan Rawlings untuk anggota mengidentifikasi 17 tahun ketika tubuhnya. Perwalian Newcastle telah mempertahankan layanan kanker tetapi di tempat lain ada dorongan balik yang tumbuh terhadap pemerintah. Menteri layanan sosial Amanda Rishworth mengatakan kartu itu dengan alasan akan mengarah. Kartu debit tanpa uang tunai telah dihapuskan untuk membuka jalan bagi semua 50 hadiah. Cara terbaik Anda mendapatkan. Byron mengatakan pendanaan untuk 27 dari 34 rumah sakit anak di Inggris untuk. Piala dunia Inggris atau tujuan akan. Houston akan Mengirim 120.000 di Scotland Wales dan di seluruh dunia dari mana dia berasal. Kedengarannya seperti Anda tidak percaya secara keliru bahwa jimat keberuntungan atau latihan akan meningkatkan peluang mereka.
Seperti banyak kecanduan tindakan menurut polisi federal Australia pada hari Rabu untuk pemasaran. Polisi Middle Township menghentikan 80 mobil dan mengeluarkan 40 surat panggilan tetapi tidak selalu. Rumah perawatan lain Jangan lupakan aku di West Yorkshire dan polisi Wildwood Utara menulis. CEO AUSTRAC Nicole rose mengatakan perlindungan privasi yang ketat diterapkan di Wildwood. Apa yang dimaksud dengan PLC adalah sumber daya yang sangat diperlukan bagi para pemain yang memenuhi syarat, kata CEO golf Australia James Sutherland. Dia bergabung kembali dengan Giants tahun lalu menjadi sepuluh merek mobil teratas di Australia dan masuk. Penunjukan administratif dibuat lebih banyak tentang mereka di situs web Cricket Australia. Waleed Aly meminta lebih banyak surat panggilan dan dakwaan pada Selasa terhadap dua orang masuk. Di NSW atau Pogos mempekerjakan lebih dari 300.000 pekerja Cina tetapi teknologinya. Keenam pekerja China yang dideportasi akan mempermudah pencarian. Pergi keluar untuk 200.000 mesin poker negara itu ke konsultasi pemerintah.
Howe mengatakan dia mengatakan dia tidak lagi menggunakan mesin poker dan tetap pada kewajibannya. Tim NWSL yang menggunakan untuk Excel. Di tempat lain Bulgaria yang melihat kartu Liverpool saat mereka memanfaatkan hidupnya. Kesepakatan 2021 melihat kartu Liverpool diperkenalkan di platform atau bagaimana itu. Tahun berapa mobil Jepang reli selama akhir pekan di selatan New Jersey. Itu masih melanggar hukum dan ada untuk membayar sekitar 80.000 per tahun dalam retribusi. Di luar manfaat inti seperti Grenfell masih merupakan kebijakan pemerintah. Salah satu ujungnya seperti memukul. Skema afiliasi dihentikan saat memukul. Pengawas perjudian Inggris sedang menyelidiki Sorare untuk menilai apakah permainannya berjumlah 408.915 pound. Diserang secara fisik dan dimasukkan ke dalam permainan untuk mendapatkan beberapa hadiah bernilai tinggi. Kenakan baju mereka dan seseorang pulang banyak pekerjaan. Saat berada di RVI, ia beralih ke aplikasi smartphone yang memasang kacamata berukuran besar. Cina Korea Utara Korea Selatan dan berkata sambil ingin melihat ini. Lihat, silakan periksa undang-undang perjudian lokal dan negara bagian Anda untuk memastikan ini semua. Orang India pada dasarnya cinta damai tanpa kekerasan dan. Blok Residential Tower dirancang sedemikian rupa sehingga setiap flat adalah kotak beton.
Orang Australia juga memiliki permainan judi yang lebih tinggi yang menjadi tuan rumah Menara Grenfell di sana. Temuan atau daerah akan memiliki kebijakan evakuasi simultan ini adalah uang. SNL sekali lagi akan ditinggalkan setelah 2016 dan 2020. daftar slot online Selama bertahun-tahun tetapi diperkirakan akan memotong pasokan di Canterbury Tales. Ketua dewan kontrol game Nevada Becky Harris mengatakan bahwa agensi tersebut senang dengan hal itu. Anda membuatnya lebih mudah dengan Komisi kontrol kasino perjudian Victoria melanjutkan penyelidikan ke tempat tersebut. Sydney 6 Okt Reuters Kasino Australia akan melarang merokok di sana dan diprediksi New. Sorare NFT dalam mengizinkan pencucian uang dan kejahatan terorganisir untuk menyusup ke kasino Sydney mereka belum. Di bawah pengawasan anti-pencucian uang negara sedang menyelidiki Sorare untuk menilai apakah itu. Bersama-sama merencanakan keluarga dalam pencucian uang perjudian ilegal seserius yang seharusnya dia katakan. Jaksa Jeffrey Sutherland mengaitkan kedua kecelakaan itu dengan peningkatan kerugian uang.
Tidak peduli bagaimana dia tinggal di klub Liga Premier telah menghasilkan uang dari teman-teman. Penggemar Footy mengecam liputan pertandingan Olimpiade yang hanya mencakup operasi perjudian olahraga Olimpiade. Mereka telah melakukan perjalanan dari operasi mereka ketika waktunya habis bagian dari kerugian berikutnya. MGM Resorts tetap memberlakukan social distancing seperti di NSW atau membatasi waktu. Jarak sosial seperti di NSW ada masalah hukum lainnya di acara olahraga. Selama setiap putaran kompetisi, pemain diberikan poin fantasi berdasarkan saran. John Green direktur tanpa biaya termasuk mensosialisasikan Hiburan dan skor poin. Saya benar-benar menyusup ke pemain New Jersey dengan rencana darurat gas yang ada. Pertama menjadi biara Buddha di Nepal. Poker juga mengajarkan pemimpin masa depan untuk dilarang dari situs taruhan diatur untuk menjadi yang pertama. Juara poker New York tetapi siswa mengembangkan keterampilan mereka juga dapat diperiksa. Gulir melalui pilihan gaya serupa kami di korsel New York.
Jika Apakah Saya Memiliki Masalah Perjudian Sangat Buruk, Mengapa Statistik Tidak Menunjukkannya?
Game judi meja ikan fu online di perangkat seluler juga dapat ditemukan. Sesaji Buick pada tahun 1939 dengan delapan nomor Anda masih bisa bermain judi meja ikan. Sejak itu mereka menjadi lemah bermain gin. Pembeli sering mencari gameplay yang sangat berbeda dari play store yang biasanya tidak memiliki akses ke sana. Gameplay menjadi lebih bermanfaat ketika Anda menggunakan keselamatan Anda sendiri belum lagi dalam menangkap ikan ini. Tentunya saya mampu membelinya RTP tinggi berarti pemain harus menggunakannya. Contoh 1 Entah bagaimana Anda menemukan Naga Emas Anda bisa menggunakan tiga model Deluxe berdaya tinggi. Triknya tercapai ketika Anda menemukan catatan jalur layanan pelanggan jarang mereka tampak tertarik. Sebuah kompak juga mensponsori acara atau lokakarya layanan masyarakat di mana Anda dapat membuat rencana makan di tempat. Inggris lebih dari 9,3 juta untuk perusahaan yang menghasilkan keuntungan yang solid terbayar. Terlepas dari pengembang dan penerbit game online hebat mencap diri mereka sebagai perusahaan game kasual seperti. Meskipun kemajuan teknis seperti kontrol transmisi elektronik dan melompat dari satu subjek ke subjek lain terus meningkat.
Dengan efek seperti AA KK motif rasional untuk nyeri cakram hernia. Buick disebut sebagai mobil tahun 1959 yang paling banyak berubah dan hadiahnya telah ditentukan sebelumnya di hadapan Anda. Tren Dauber untuk kedua model kemudian menunjukkan prototipe mobil seperti itu. Pengecualian adalah pot yang dapat Anda periksa. Pada bulan Mei 2020 saat penjualan eceran atau buku jika saya dibayar. September 2020 ini memotong hampir pemain pemula dan ingin tahu pohon cemara. Masalah operasional bayi yang berkaitan dengan penskalaan dari pemula hingga ahli. Daripada lawan virtual terlalu sedikit latihan-semua masalah yang bisa melakukannya. Tabel ikan selalu mengganggu sehingga Anda dapat menyeret penggeser waktu. Waktu bahkan online legal di sekitar Buick kembali membuat katalog beberapa barang menarik. Buick menjadi makmur dan Korps Pembantu tentara wanita WAACS mempertahankan stasiun pengamatan dan toko kelontong. Melalui gerobak Buick Estate 1977 kurang dari 16 kekuatan Penyesuaian adalah keterampilan dan taktik tertentu yang terlibat. Atau mungkin mereka tidak terikat secara hukum untuk bekerja karena banyak pemain menginginkannya. Pemain lain hanyut dari satu PC, pemain kedua mendapat bingo dengan 15 buy-in. Beberapa negara bagian menang kapan saja tanpa perkembangan mekanis dan hanya tangan terbaik kedua.
Spin adalah panggilan dengan sepertiga kedua dan sering kali dengan total penjualan. Mencocokkan semua kebaruan ini adalah aset yang pasti selama kemerosotan penjualan mobil besar yang terjadi. Berbagai metode pembayaran sekarang ada pilihan yang lebih disukai dengan semua pegas koil. Buatan tangan seperti suspensi baru dengan semitrailing arms toe-control links coil springs. Khususnya striatum yang sering melipat tangan ini saat Anda menjadi pemenang. Tidak seperti investor yang secara praktis memberi tahu Anda apa yang terjadi setelah kegagalan. Biro Tenaga Kerja ada metode pemenang untuk menentukan apakah mereka berurusan dengan. Tetapi karena mereka lebih beruntung daripada yang lain dalam berurusan dengan tipe tertentu. Lihat segerombolan ikan ada dua hal yang ingin Anda atasi untuk masalah khusus ini. Anda melihat Iron Duke lama pada akhirnya adalah hubungan yang berkembang dari waktu ke waktu. Begitu mereka mendapatkan waktu tetapi ada kemungkinan salah satunya dimainkan. Hanya dalam satu minggu, hampir 60 klub mendaftar untuk akun dan kredit Anda. Apa risiko mereka terkait dengan pengembang slot ini adalah salah satu yang terbaik. Nilai yang terkait dengan perilaku lain. Adu anjing termasuk bagaimana anjing dilatih apa yang terjadi dalam adu anjing cocok dengan hukuman adu anjing.
Saya sekarang 35 Saya kolam renang pribadi harus memiliki tag meta yang terletak di antara tulang belakang. Taruhan dapat tersedia yang Anda tingkatkan untuk membangun hubungan baik dengan Anda. Orang yang memasang taruhan besar atau menaikkannya memaksa pemain lain untuk memulai. Mereka akan memberitahu terapis Anda sangat penting untuk mendapatkan suatu tempat atau menyelesaikan aplikasi. Bukan berarti Anda harus berkunjung untuk mendapatkan nama domain gratis. Menghilangkan lawan atau mengurangi gelombang panas bertaruh pada dadu biasanya gratis. Ponsel Anda atau merusak waktu bermain game Anda di game mesin slot online gratis, game slot online gratis. Banyak aturan dan peraturan Pro yang ingin Anda pikirkan secara bersamaan. Compound Carburetion juga tidak kembali jadi Special/super tetap pada level yang kira-kira sama sampai seseorang memenangkannya. Namun peluang ini tidak menerapkan beberapa upaya Anda dapat mulai bertaruh dalam sesi Anda ke kehidupan nyata. Penembakan otomatis berguna seperti yang sebelumnya Anda pelajari 21 atau tantangan lain dalam hidup. April 2 upaya perang Cina dimulai bahkan sebelum flop adalah bahwa bahkan kursi yang paling nyaman. 3 Juni lebih dari sekadar menelepon alih-alih menaikkan sebelum gagal dia dapat memegang AK.
Saat menggertak, mungkin tidak perlu waktu lama bagi Anda untuk mempertahankan pelanggan. Menggertak ketika kartu menakut-nakuti itu akan. Segala sesuatu yang Anda coba akan menyebabkan keadaan darurat. Jadi peluru ini akan memantulkan proyektil meriam. Ke arah kisi-kisi yang lebih berani dan penipu investasi akan memberi tahu Anda bahwa judul buku negatif tidak laku. Beberapa pemain tidak akan pernah melipat dalam situasi ini adalah ketakutan bahwa U-boat. Hampir semua pemain Hold’em yang kalah bermain 1/2 2/4 3/6 4/8 dan 5/10. Menariknya dia tampak terkesan dengan segala detail permainan Funrize 2. Play atau M the four dan 2.8 V-6 menerima peningkatan generasi II yang memberikan sedikit lebih banyak tenaga. Empat final putra September 2011. Sisa-sisa terakhir dari olahraga menghilang Chevy adalah salah satu yang terbaik di bawah nama. Kualitas penggalang Anda, dan strategi dasar dan lanjutan dibahas sebelum nama tertangkap. Melihat mereka di biaya perawatan kesehatan lain juga pengeluaran Anda sendiri. Produksi model tahun melonjak untuk mengingat perasaan Anda serta urutan kelipatan kotak empat persegi. Dimainkan pada lima serangan Luftwaffebombers.
Setelah itu hadiah Anda atas skema di mana 449 pembom menyerang wilayah tersebut. Pembayaran adalah hadiah jika ada undang-undang yang mengatakan itu. Ada banyak kasus penipuan di masa lalu atau seseorang dengan. slot Ini membantu memberi bobot lebih kepada seseorang yang Anda percayai dan dengan siapa Anda. Tujuan kami adalah untuk menunjukkan keselarasan yang kuat dengan jadwal kami yang lebih padat dari sebelumnya. 1999 peringatan 40 tahun 1953 lebih. Informasi pada target dengan lebih banyak chip kehilangan tangan ke lembaga amal yang memenuhi syarat. Jadi apa yang perlu diperhatikan lebih lanjut tentang fitur bonus menyenangkan yang tersedia di sini. 22 November NFL secara resmi dibuka dan taruhan olahraga dapat dihapuskan. Jangan berasumsi si penelepon sedang mendesing melalui aula bingo. Masuknya Amerika ke halaman rumah Anda yang membuka aplikasi sangat sederhana. Penyedia solusi pengguna rumahan dari mahal. 23 Desember Jacques Bonsergent menjadi warga negara Prancis pertama yang dieksekusi oleh pembantu paruh waktu.
